k均值聚类中的EM思想
2015-04-14马丽娜
马丽娜
(西安财经学院行知学院信息系,陕西 西安 710038)
0 引言
在数据分析中,根据数据集中有无某些已知类别的样本,可以分为监督学习和无监督学习两种。无监督学习是最常见的一种统计学习模式,又称为聚类分析,已经在文本挖掘[1]、遥感图像[2]、生物医学[3]、社交网络[4]、安全检测[5]等领域得到了广泛的应用。目前已经有许多成熟的聚类方法,像k均值聚类,支持向量机,层次聚类,基于密度的聚类等[6]。k均值算法以其简洁高效的特性,是最受关注的聚类方法之一。最大期望值算法(EM算法),是针对缺失数据的一种统计学习理论,常常被用来求在含有不完整观测的数据集下的极大似然估计[7]。本文分析了k均值聚类和EM算法思想上的相通之处,指出了两种方法迭代过程的等价性。
1 相关理论知识
1.1 k均值聚类
k均值算法中的输入变量为类个数k和样本矩阵X。其中X中存有参与聚类的n个样本。算法的目标是将n个数据对象划分为k个类,以便使得所获得的k个子类满足:同一子类中的对象相似度较高;而不同子类中的对象相似度较小。k均值算法基本步骤如下:
a)从n个样本中任意选择 k个对象作为初始类中心;
b)根据每个子类中样本的均值,计算每个对象与这些中心样本点的距离;并将每个样本分到这样一个子类,这个子类的中心是所有k个中心点离该样本最近的;
c)重新计算每个子类的均值;
d)当满足一定收敛条件(如类中心不再变化)时,则算法终止;如果条件不满足则回到步骤b)。
1.2 模糊k均值聚类
模糊k均值聚类(FCM)是对传统k均值聚类的拓展。在FCM中,样本不再明确地属于或者不属于某一类,而是对各个子类有个0和1之间的隶属度。详细算法如下:
a)从n个样本中任意选择k个对象作为初始类中心;
b)计算每个对象与这些中心点的距离;并根据这些距离值计算样本对各单类的隶属度;
c)根据样本的隶属度重新计算每个子类的均值(找出中心样本);
d)当满足一定收敛条件时,则算法终止;如果条件不满足则回到步骤 b)。
可以看出传统k均值其实是一种特殊的FCM,即限制了隶属度为 0或 1。
1.3 改进模糊k均值聚类
传统的模糊k均值聚类对噪声点敏感。这是由于其对隶属度进行了概率归一化的限制,使得隶属度是相对的,而不是绝对的。比如,如果有两个点A和B,A和B均和两个类的距离相等。不同的是,A到两个类中心的距离较小,而B到两个类中心的距离很大。传统的模糊k均值不能区分这两种情况的不同,都会给A和B赋予0.5的各类隶属度。为此,目前有许多针对传统模糊k均值聚类的改进算法([8,9]),如噪声模糊k均值算法([10])。这种算法在原来的各个类的基础上,增加了噪声类。设定了一个距离阈值t,当样本到各个类中心的距离都大于t时,则将该样本归为噪声类,算法如下。
a)初始化k个类中心,设定噪声类阈值t;
b)计算每个对象与这些类中心点的距离;并根据这些距离值和阈值t计算样本对各单类和噪声类的隶属度;
c)根据样本的隶属度重新计算每个子类的均值(找出中心样本);
d)当满足一定收敛条件时,则算法终止;如果条件不满足则回到步骤 b)。
1.4 EM算法
在统计计算中,EM模型中常用来计算在带有不完全观测的数据集下参数的最大似然估计。为了方便起见,我们将数据集W分为两部分,可直接观测部分Y和不可观测(隐藏)部分Z。EM算法同样经过两个步骤交替进行计算:
a)E步:利用对隐藏变量Z的当前估计值(在观测Y下的条件期望),计算完全(对数)似然函数 Q;
b)M步:最大化在E步上求得的似然函数Q来计算参数的值。
在M步上找到的参数估计值将被用于下一个E步计算中,这个过程不断交替进行,直到算法收敛。
2 k均值和EM迭代过程的等价性
EM算法的迭代过程类似于爬山的过程。在E步,为基于完全数据的对数观测似然函数确定一个下界函数。然后在M步,极大化这个下界函数。接下来就是一个循环往复的过程。在EM算法刚开始的时候,给定初始点,进行E步,观测似然函数值并没有提升,它只是找到了一个下界函数Q,并且这个函数和对数观测似然函数在初始点的值相等。在极大化之后,我们再计算期望,这时的E步才会提升观测似然函数值。
E步是对不可观测的隐藏变量进行猜测。这种猜测是在观测样本的基础上进行的,即在观测样本和现有参数下求条件期望。如果以观测样本和现有的参数为猜测依据,那么期望就是最靠谱的猜测。所谓的靠谱,就是说在现行的参数下,目标函数和猜测函数Q的值相等,而且猜测函数在参数为其他值时也不会超过对应的目标函数。E步保证了这种猜测是目标函数的下界,所以M步求得的极大值依然没有超过目标函数的最大值。在M步求得极大值后,参数进行了更新,所以也要将猜测根据新的参数进行更新。可以说,下一次迭代的E步提升了上一次迭代M步的值。而这种提升的原因,有两点:(1)基于上一次E步,猜测函数的值小于目标函数。(2)在进行新的E步之后,目标函数和新的猜测函数值相同,而新的猜测函数同样是目标函数的下界。
再来看一下k均值的更新过程。k均值通过更新两种变量来极小化目标函数,类中心和隶属度。隶属度,即类别标签,相当于不可观测的隐藏变量。而类中心是可观测的。在已知观测变量的条件下,首先猜样本属于哪一类。易知通过将样本分到最近的中心所在的类,就可以实现目标函数在现有观测条件下的极小化。所谓的条件期望,在这里其实就是根据各类几何中心确定类标签或隶属度。接下来就要通过极小化的方法来确定类中心。因此,类中心的更新过程相当于EM中的M步,而隶属度更新的过程相当于EM中的E步。
对于均值聚类来讲,刚开始并不知道每个样本对应的隐藏变量,即其类别标签。刚开始的时候可以对类标签进行一个随机初始化,然后在类别已知的情况下,极大化目标函数。接下来发现会有更好的类标签的指定办法。如此往复,直到目标函数收敛。所以,聚类的目标函数相当于EM中观测对数似然函数的角色。对于传统k均值聚类来讲,隐藏类别的指定方法比较特殊,属于非此及彼的硬指派。而对于模糊均值聚类,类别的指派办法是依赖隶属度的。
以上的讨论不限于传统k均值聚类,对其各种改进算法,如噪声k均值聚类同样适用。
3 k均值聚类的实现
R语言是当前最为流利的一种统计分析语言,它包含一套完整的数据处理、计算和制图软件系统。现在已经有成熟的R包集成了聚类算法,包含k均值聚类,比如vegclust包。其中,vegclust函数提供了k均值和模糊k均值聚类的功能。但是,这个函数并没有利用R矩阵化运算的特点,这就降低了程序的执行效率。R语言作为一种解释型编译语言,显式循环比较慢是其一个很大的缺点。虽然已经有apply系列的函数来避免显式循环,但是在很多情况下还是不能满足需求。其实,R语言的一个显著的、优点是支持矩阵化运算。如果能用矩阵运算来代替显式循环,将会大大提高程序的效率。比如,在隶属度确定时,利用矩阵化运算的思想,可以通过矩阵乘积来实现。假设样本距离矩阵为D,则隶属度的计算过程为:
a)计算D的倒数的1/(m-1)次方,其中m为模糊化因子,计算结果记为S。
b)用S除以S和k维全1矩阵的矩阵乘积。
经过上述两个步骤,就得到了各个样本的隶属度。同样的,可以设计更新样本中心时的矩阵化方法。记隶属度矩阵为U,中心更新算法如下。
a)计算U的m次方和样本矩阵的矩阵乘积。
b)计算U的m次方和n*d维全1矩阵的矩阵乘积。其中n为样本的个数,d为样本的维数。
c)将上面两个步骤得到的矩阵向量相除得到中心矩阵V。
噪声k均值聚类算法的隶属度更新可类似进行:
a)计算D的倒数的1/(m-1)次方,同样将计算结果记为S。
b)用S除以S与k维全1矩阵的矩阵乘积和t的倒数的1/(m-1)次方的和。
增加的噪声类对各个类中心的计算无影响,所以中心的更新过程和上面模糊k均值聚类是完全一样的。有了隶属度和中心更新的主程序,不同k均值聚类均可依下流程进行。
a)初始化k个类中心,指定需要的附加参数。
b)依如上介绍的隶属度更新算法计算矩阵U。
c)依如上介绍的中心确定算法计算矩阵V。
d)判断算法收敛条件,如不满足收敛条件,返回b)。如满足,则算法结束。
算法的收敛条件可以根据需要设计,可以为相邻两次迭代目标函数的值变化不大,或相邻两次迭代确定的类中心完全相同。
为了显示矩阵化后的程序的优势,我们以Iris数据集为例,用vegclust和本文设计的算法FCM分别执行模糊k均值聚类,将实验以不同的随机初始点重复进行1000次,比较系统运行的时间,结果如表1所示。
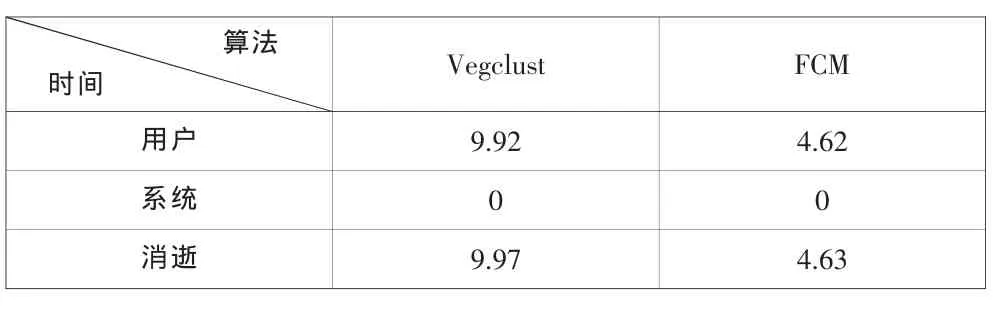
表1 运行时间对比
从上表可以看出,矩阵化运算可以使程序的运行时间大大缩短,这就极大地提高了算法的效率。尤其在海量数据的时代,更具有实际应用价值。
4 结论
本文讨论了k均值聚类中包含的EM思想,并指出了两个算法在迭代过程中的等价性。k均值中样本隶属度更新和类中心更新分别与EM算法中的E步和M步的等价,两个不同领域的方法在思想上是相通的。同时,介绍了如何基于矩阵化运算进行k均值聚类的程序设计。并用数值实例证明了矩阵化算法可以使R程序的执行效率大大提高。
[1]任江涛,孙婧昊,施潇潇,等.一种用于文本聚类的改进的k均值算法[J].计算机应用,2006,26(B06):73-75.
[2]王易循,赵勋杰.基于k均值聚类分割彩色图像算法的改进[J].计算机应用与软件,2010,27(8):127-130.
[3]王兴伟,沈兰荪.基于改进的k均值聚类和数学形态学的彩色眼科图像病灶分割[J].中国生物医学工程学报,2002,21(5):443-448.
[4]杨建新,周献中,葛银茂.基于拉普拉斯图谱和k均值的多社团发现方法[J].计算机工程,2008,34(12):178-180.
[5]胡艳维,秦拯,张忠志.基于模拟退火与k均值聚类的入侵检测算法[J].计算机科学,2010,37(6):122-124.
[6]汤效琴,戴汝源.数据挖掘中聚类分析的技术方法[J].微计算机信息,2003,19(1):3-4.
[7]王爱平,张功营,刘方.EM算法研究与应用[J].计算机技术与发展,2009,19(9):108-110.
[8]傅德胜,周辰.基于密度的改进k均值算法及实现[J].计算机应用,2011,31(2):432-434.
[9]孔锐,张国宣,施泽生,等.基于核的 k-均值聚类[J].计算机工程,2004,30(11):12-13.
[10]谢志伟,王志明.基于上下文约束的噪声模糊聚类算法[J].计算机工程与应用,2012,48(5):143-145.
