单层球面网壳的整体稳定性分析①

汤 欢，沈之容

(同济大学土木工程学院，上海200092)

0 引 言

自20 世纪60 年代以来，网壳结构的非线性稳定研究一直是国内外学者关注的热点问题，这些研究工作的内容大致可分为以下几方面:网壳结构大位移几何非线性和单元弹塑性变形分析方法研究，网壳结构对初始缺陷的敏感性和网壳结构极限承载能力研究，大型网壳结构稳定性试验方法探讨以及全过程分析程序的编制等［1］.

本文就是在这一基础上，利用大型通用有限元软件ANSYS，以肋环型单层球面网壳为代表，进行了几何非线性整体稳定分析和弹塑性整体稳定分析.考察了网壳初始缺陷的有无、初始缺陷的选取、以及杆件划分的单元数量对其整体稳定的影响.

1 网壳结构整体稳定性的分类

图1 有限元模型

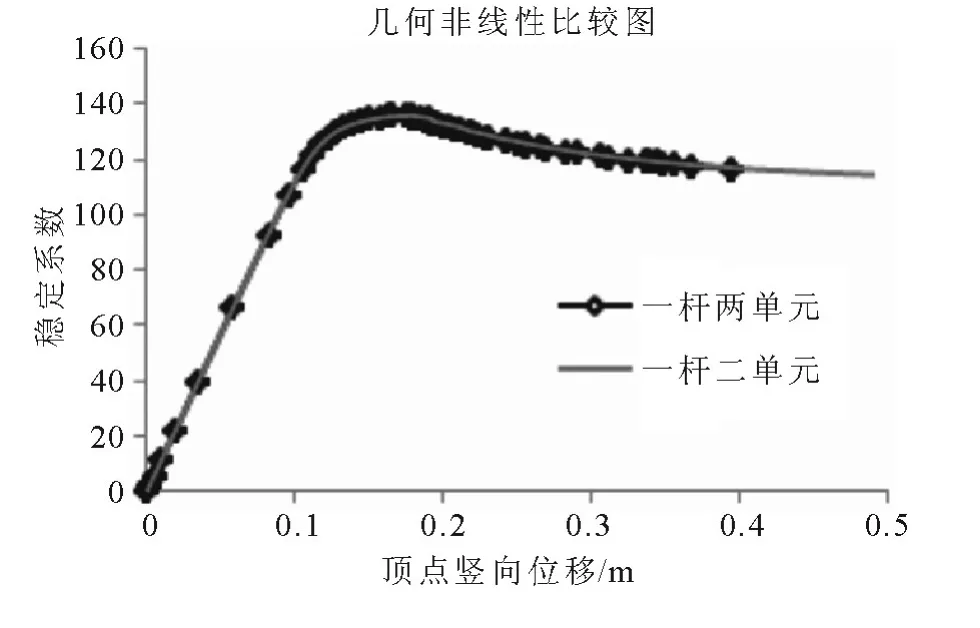
图2 大位移几何非线性荷载－位移曲线

网壳结构的整体稳定分为三种，分别为线性整体稳定、弹性几何非线性整体稳定、弹塑性整体稳定，而弹塑性整体稳定又分为完善结构和带缺陷结构整体稳定.三种结构整体稳定系数中，线性整体稳定系数计算简单，临界值偏高，属于稳定的上限;弹性几何非线性整体稳定系数适合于弹性工作状态的结构(较柔结构)，但对于失稳处于弹塑性状态的结构，临界值偏高;弹塑性整体稳定分析能够得到符合实际的临界值.特别对于相对较刚的结构体系更为适用［2］.

2 有限元分析

2.1 有限元模型

(1)结构及材料参数

单层球面网壳，跨度60m，矢跨比f/L =1/2(半球壳);网壳采用肋环型.纬向划分30 段，径向划分12 段;构件采用圆钢管，钢管截面参数如下:

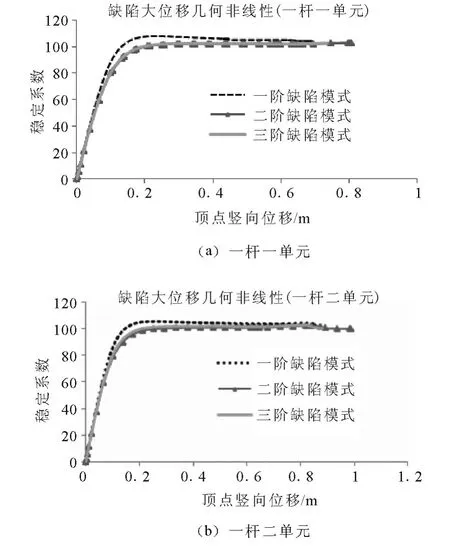
图3 三种缺陷模式下几何非线性荷载－位移曲线

肋杆:φ245×8 纬杆1 ～4 层:φ245×8;纬杆5～8 层:φ203×8 纬杆9 ～12 层:φ186×6;网壳周边边界点为支座节点，且为固定铰支座.

圆钢管采用Q235B，密度为ρ = 7.85 ×103kg/m3，屈服强度为fy=235MPa，弹性模量为E=2.06×105MPa，泊松比υ=0.3.

(2)荷载条件

均布恒载(q):q =0.3kN/m2(不包括结构自重)均布活载(p):p=0.5 kN/m2

荷载组合:1.0 恒+1.0 活，活载满跨.

荷载施加方式为单参数同步加载.(3)单元选取及网格划分

计算模型分为一杆一单元模型和一杆两单元模型，由于是单层网壳，单元采用ANSYS 中的BEAM188 单元，有限元模型如图1 所示.

2.2 有限元分析

(1)完善结构的大位移几何非线性分析

进行完善结构大位移几何非线性整体稳定分析时，将荷载放大200 倍，打开几何大变形开关，采用弧长法迭代求解，网壳顶点竖向位移达到1m时，迭代停止，网壳的大位移几何非线性荷载－位移曲线如图2 所示.

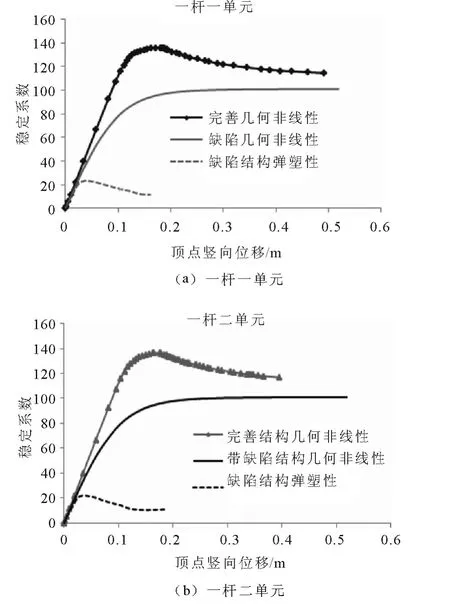
图4 三种结构荷载－位移曲线对比

由图2 可知，完善结构大位移几何非线性分析荷载位移曲线的第一个极值点所对应的，一杆一单元与一杆两单元模型的稳定系数相差不大，都取135.96.

(2)带缺陷结构非线性整体稳定分析

网壳结构的初始几何缺陷模式，根据“一致缺陷模态法”，分别取线性整体稳定分析得到的第一、二、三阶屈曲模态模拟.缺陷幅值按《空间网格结构技术规程》(JGJ7－2010)［3］确定，为L2/300(L2为网格结构短向跨度).故取缺陷幅值为60000/300=200mm，跟踪计算网壳结构的屈曲平衡路径全过程，得到带缺陷结构大位移几何非线性荷载－位移曲线如图3 所示.

(3)带缺陷结构的缺陷敏感性分析

(4)带缺陷结构弹塑性整体稳定分析

在对结构进行带缺陷结构大位移弹塑性整体稳定分析时，选取缺陷模式为第二阶线性屈曲模态，缺陷幅值取200mm，定义材料为理想弹塑性材料(无强化阶段)，跟踪全过程，并将完善结构和带缺陷结构的大位移几何非线性整体稳定分析以及带缺陷弹塑性整体稳定全过程的荷载－位移曲线反映在同一坐标系中，如图4 所示:

3 计算结果

根据上文分析得到的网壳完善结构几何非线性稳定系数、缺陷结构几何非线性稳定系数、缺陷结构弹塑性整体稳定系数，结合完善结构的几何非线性稳定系数(前文未给出)，汇总后由表1 给出.

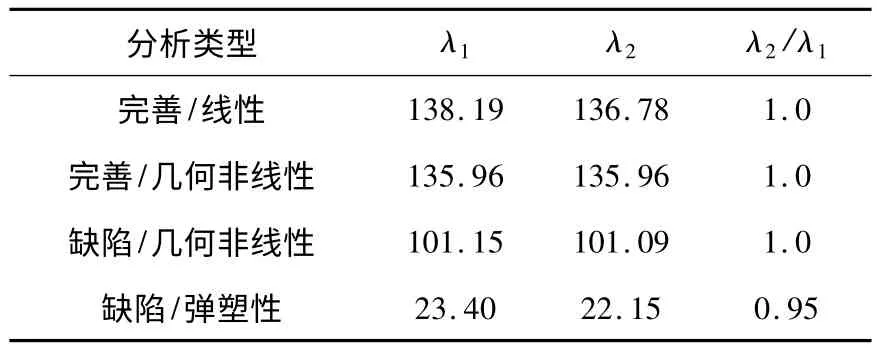
表1 不同单元数模型整体稳定系数比较汇总

其中，λ1为一杆一单元模型对应的稳定系数，λ2为一杆二单元模型对应的稳定系数，由表1 可知，网壳的缺陷敏感性系数

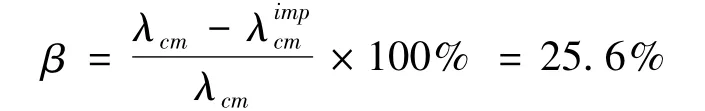
4 结 论

本文针对单层肋环型跨度60m 球面网壳进行了线性整体稳定、完善(缺陷)结构几何非线性整体稳定和带缺陷结构大位移弹塑性整体稳定分析，分析了不同类型稳定性特点，得出结论如下:

(1)四种屈曲分析结果中，完善结构大位移几何非线性稳定系数与线性屈曲的结果相差很小，带缺陷结构几何非线性稳定承载力较完善结构下降明显，约25.6%，缺陷结构弹塑性稳定承载力较几何非线性稳定承载力下降非常大，约77%，一旦结构进入屈服状态，它的稳定承载力将急剧大幅下降.

(2)“一杆两单元”模型的稳定承载力相比于“一杆一单元”模型的稳定承载力几乎没有下降，出现这种现象的原因可能是，结构的网格划分较小或杆件截面取值过大，使得构件的局部失稳荷载始终高于整体失稳荷载.

(3)虽然结构满足《网壳结构技术规程》(JGJ7－2010)规定的带有初始几何缺陷的结构在荷载标准组合作用下，由弹性大位移几何非线性分析得到的最小(或第一个)整体稳定临界荷载系数不小于4.2，但在几何非线性分析过程中，当荷载达到整体稳定最小临界荷载因子时，网壳构件出现屈服变形现象，故因进行缺陷弹塑性分析.

［1］ 曹正罡，范峰，沈世钊.单层球面网壳的弹塑性稳定性［J］.土木工程学报，2006，(10).

［2］ 罗永峰，韩庆华，李海旺.《建筑钢结构稳定理论与应用》［M］.北京:人民交通出版社，2009.

［3］ JGJ7－2010《网壳结构技术规程》［S］.北京:中国建筑工业出版社，2003.

［4］ 沈世钊，陈昕.《网壳结构的稳定性》［M］.北京:科学出版社，1999.

［5］ 王新敏.《ANSYS 工程结构数值分析》［M］.北京:人民交通出版社，2009.