基于模糊识别的地下水评价

张钟元

(黑龙江省水利水电勘测设计研究院，哈尔滨150080)

0 引言

了解中国的地下水水质状况，根据地下水水质现状评价成果，密切结合污染源种类、物质组成和地理分布特征，通过综合分析，确定污染范围，并探讨地下水污染的成因。至今为止，国内外学者做了大量的研究，依据《地下水质量标准》(GB/T1448－93)，提出了很多的地下水水质评价的方法，比如BP神经网络模型、灰色关联聚类、熵权的模糊物元、模糊综合评判法、相关性分析方法、模糊数学法［1］等，并取得了一定的研究成果。文章结合石家庄地区2004年地下水水质统测数据的实例，应用工程模糊集理论中的二元比较方法确定权重以及模糊识别模型来进行地下水水质评价，取得较为良好的效果，模糊识别模型较其它方法相对简便，结果也较为理想。为制定地下水资源可持续开发利用政策、措施提供技术依据。

1 二元比较

设基本单元系统中有因素集公式为:

其重要性的二元对比矩阵为:

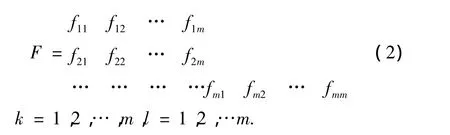
若满足条件:

1)当fhk＞fhl时，有fkl=0

2)当fhk＜fhl时，有fkl=1

3)当fhk=fhl时，有fkl=0.5

则矩阵F必须满足重要性定性排序的传递性，F称为重要性排序一致性标度矩阵，h=1，2，…，n。

2 模糊识别模型［2］

设有需要对模糊概念或模糊子集A进行识别的n个样本组成的组合，有m个指标(或目标)特征值表示样本的整体特征，则有样本集的指标(或目标)特征值矩阵:

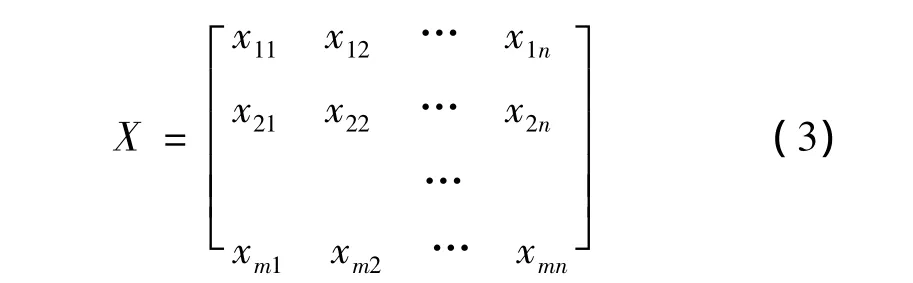
式中:xij为样本j指标i的特征值，i=1，2，…，m;j= 1，2，...，n。

如样本集依据m个指标按c个状态或级别的已知指标标准特征值进行识别，则有指标标准特征值矩阵:

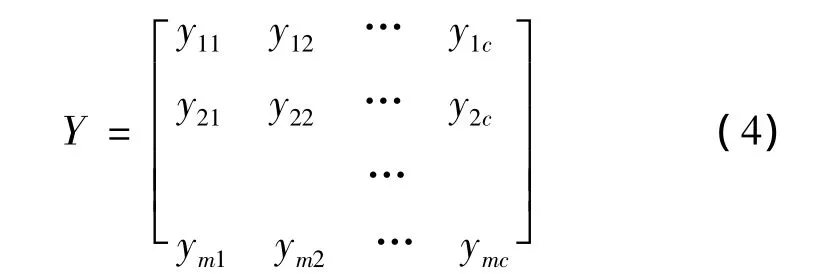
式中:yih为状态或级别h指标i标准特征值，h=1，2，…，c;i=1，2，…，m。

当指标从1级变至c级指标标准特征值增加时，指标对A的相对隶属度(隶属函数)为:

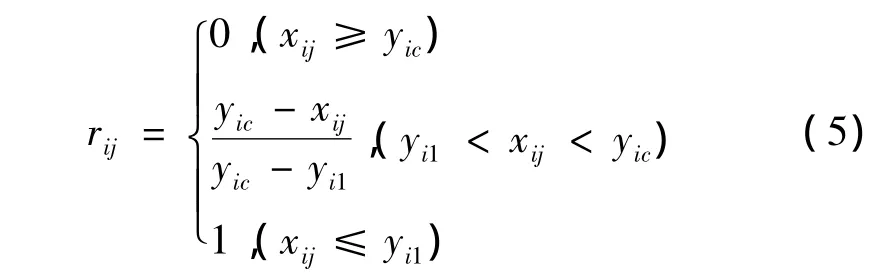
h级指标标准特征值对A的相对隶属度(隶属函数)为:

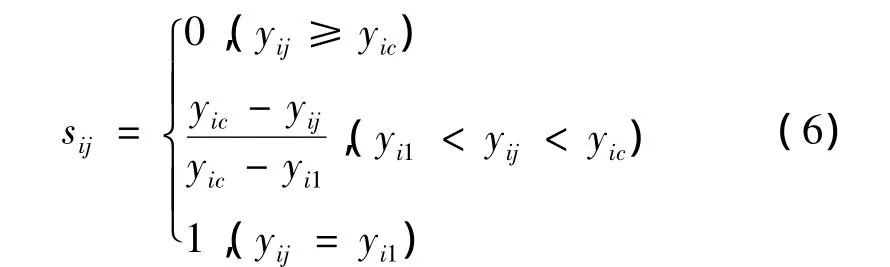
此外，指标的权重向量ω

根据拉格朗日函数，得到模糊识别模型如下

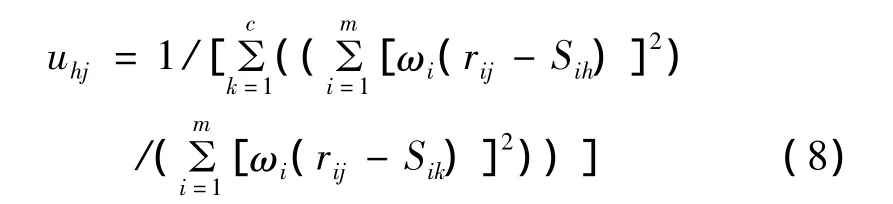
式中:uhj为样本j对级别h的相对隶属度，j=1，2，…，n;h=1，2，…，c。

级别特征值向量如下

4 应用实例

研究采用的数据为石家庄地区2004年地下水水质统测数据［9］。各评价指标分级标准见表1。

依据《地下水质量标准》(GB/T14848—93)，各评价指标分级标准见表2。

应用公式(5)将矩阵X变为相对隶属度矩阵R为:

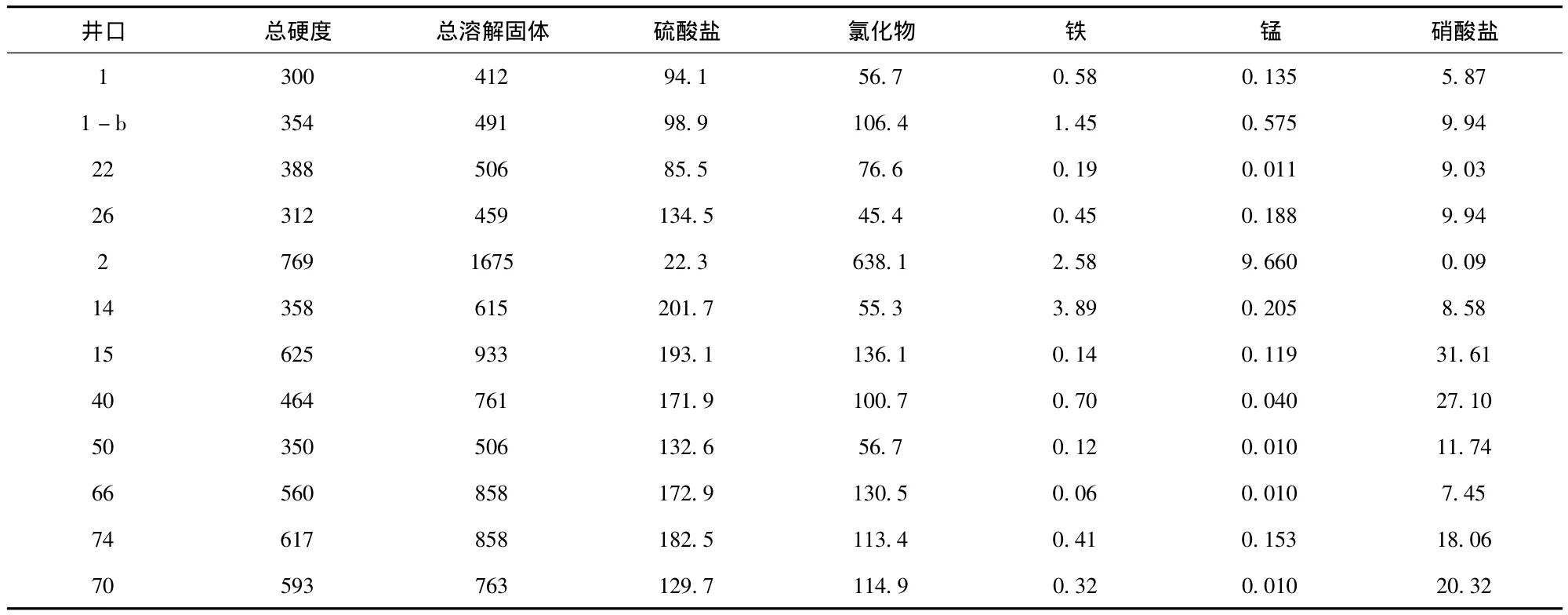
表1 研究区水质监测数据 mg/l

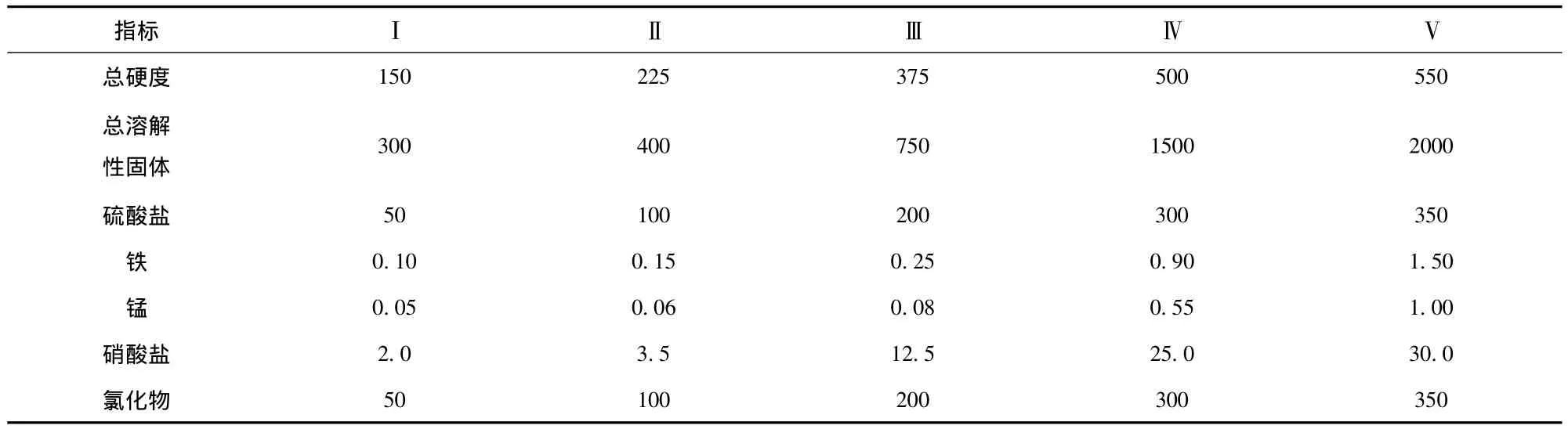
表2 地下水质量分级标准

应用公式(6)将矩阵Y变为指标标准特征值相对隶属度矩阵S为:

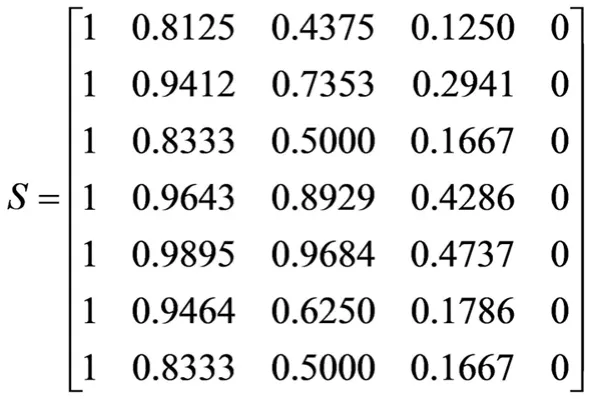
根据二元比较方法，应用公式(2)得到7项指标二元比较矩阵如下:

根据上面矩阵，确定7项指标权重向量为:

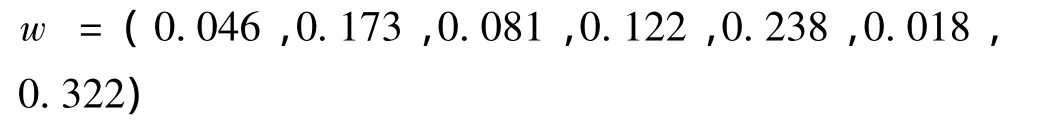
运用模糊识别模型公式(8)得到水样相对隶属度矩阵U:

运用公式(9)得到各个样本的级别特征值如下:

5 结论

从结论可以看出石家庄地区年地下水水质均处于Ⅱ－Ⅲ类中间，其中，井口5水质污染程度相对最为严重，井口1－b和14污染程度相对较为严重，井口40、1和2污染程度相对偏轻，井口26、66、15和70污染程度较轻，井口22和50污染程度最轻。文章应用二元比较方法确定指标权重以及模糊识别模型来进行地下水水质评价，方法比较简便，物理概念清晰，根据相对隶属度矩阵得到样本级别特征值，直接进行评价分析，取得了较为理想的评价结果。

［1］中华人民共和国国家技术监督局.地下水质量标准GB/ T1448—93［M］.北京:中国标准出版社，1994:67.

［2］倪深海，白玉慧.BP神经网络模型在地下水水质评价中的应用［J］.系统工程理论与实践，2000(08):124－127.

［3］杨帆，张征，吕连宏，等.基于灰色关联聚类的地下水评价指标优化研究［J］.环境工程，2008(26):304－309.

［4］王力，刘廷玺，戴鑫，等.基于熵权的模糊物元在地下水水质评价的应用［J］.人民黄河，2010，32(12):120－122.

［5］骆祖江，陆顺.模糊综合评判法在嵊泗海域地下水评价中的应用［J］.勘察科学技术，2009(04):51－54.

［6］欧亚波，李泽琴.地下水水质评价中相关性分析方法的应用［J］.广东微量元素科学，2004，14(08):18－22.

［7］郭东兴，刘运涛，杨晓双，等.运用模糊数学法评价项城地下水水质［J］.地质灾害与环境保护，2007，18(04): 105－107.

［8］邢军，付芝，孙立波.基于熵权的地下水水质模糊综合评价［J］.节水灌溉，2011(08):5－7.

［9］陈守煜.工程模糊集理论与应用［M］.北京:国防工业出版社，1998:26－28.