压缩感知在超声成像中的应用研究进展

刘敬 罗建文 清华大学 医学院生物医学工程系 （北京 100084）

0.背景

经典的香农-奈奎斯特采样定理认为，为了不失真的重建模拟信号，采样频率不能小于信号最高频率的两倍。由于只用到了信号最高频率这一先验信息，经典采样定理得到的信号有较大的冗余，导致采样信号数据量很大，不方便存储和传输。现有的数据压缩方法如有损压缩通过对采样信号进行正交变换，量化等操作，能极大的去除信号冗余，最后达到降低数据量的目的。先对信号高速采样，然后进行数据压缩，最后在接收端解码的数据获取模式已得到广泛应用。但这一模式最大的弊端是数据的浪费：高速采样得到的信号都被数据压缩大量丢弃了。

既然最后要丢弃这一部分数据，为什么开始要采集下来呢？为了解决这一矛盾，Donoho 等人提出了一种在数据采集阶段就实现数据压缩的信号采样和重建方法即压缩感知[1]。压缩感知理论指出，若一个信号是稀疏的或可压缩的，那么利用其少量投影数据，信号即可被高概率重建。根据这一特点，压缩感知已成功应用于磁共振成像，大大降低成像速度[2]。最近，压缩感知也开始应用于医学超声成像领域，根据应用特点，学者从不同角度建立了基于压缩感知的医学超声成像模型。这些研究主要集中在超声信号的压缩采样和超声逆散射问题的求解。除了基本的超声成像，压缩感知在超声CT，超声多普勒成像和光声成像中也有应用。

1.压缩感知

如何从y 中重建出x 是压缩感知研究的另一个问题。y 中元素的个数小于x，上述方程是欠定的，若没有其他条件，该方程将有无穷多个解，即不能从y 中重建出唯一的x。压缩感知理论指出，若x 是稀疏的或在某个变换域是稀疏的，那么该重建是可能的。信号的稀疏性可以表示如下：

将公式（2）带入（1），可以得到：

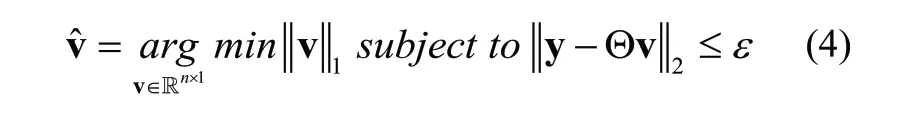
2.压缩感知在超声成像中的应用

医学超声图像的形成一般是：先控制各阵元发射多个不同的超声波束，然后对探头接收到的通道数据进行波束合成，最后进行包络提取和对数压缩等操作。由于超声图像重建的过程中信号种类多样，为了将压缩感知应用于超声成像，对什么信号进行压缩采样以及如何进行压缩采样是研究者们关心的问题。除了传统的延时叠加波束合成算法，超声逆散射问题的求解是另一种重建超声图像的方法。压缩感知理论的提出也为这一领域注入了新的活力。

2.1 超声信号的压缩采样

由上述超声图像的形成过程可知，超声信号在不同阶段的表现形式是不同的。最原始的超声信号也叫通道信号或后向散射信号。直接由接在阵元上的通道获得，数据量大；经过波束合成后的信号相比通道数据，数据量大大减少；经过包络提取和对数压缩后的信号则是构成图像的各个像素。这些信号均可进行压缩采样，而前端通道数据的压缩采样更有意义，研究的也较多。

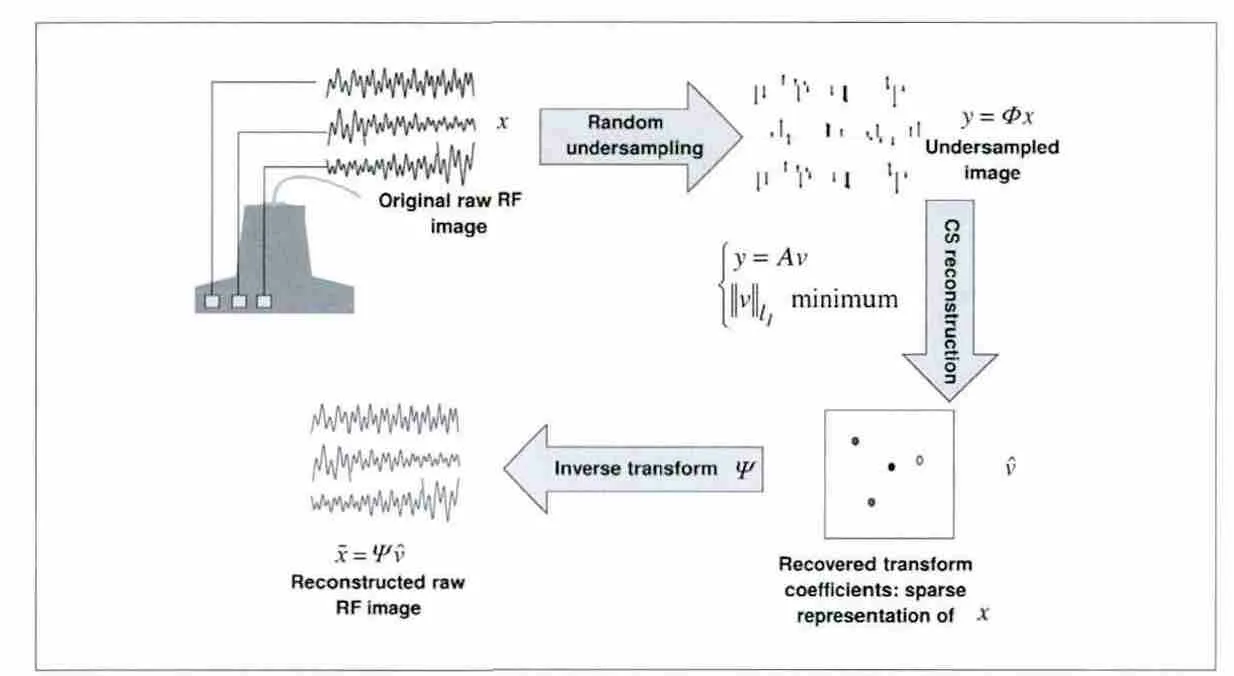
图1. 超声通道数据的采集和重建流程

图2. 不同稀疏基的重建误差随降采率的变化

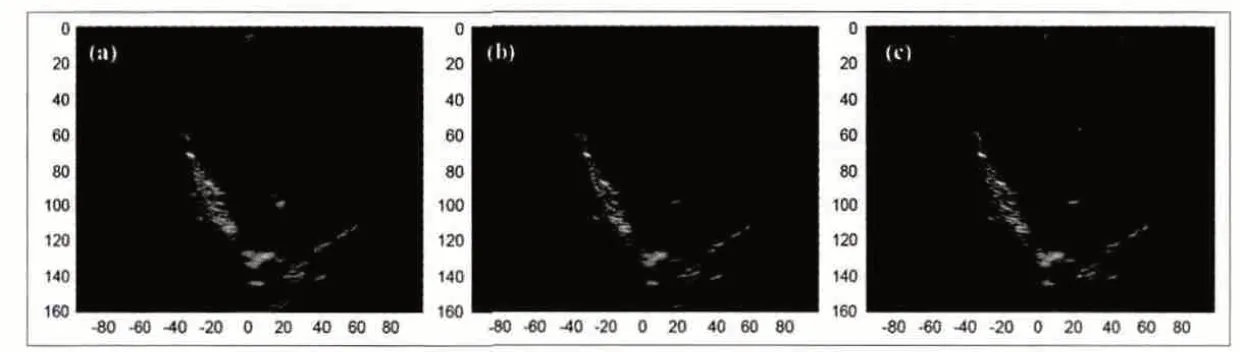
图3. Xampling 采样策略对心脏图像的重建

另外，超声信号从信号变化快慢的角度又可分为快变时间域信号（fast-time signal）和慢变时间域信号（slow-time signal）。快变时间域信号是沿深度方向的信号，慢变时间域信号是沿超声发射波束重复方向的信号。直观上，快变时间域信号的压缩采样能降低数据量，慢变时间域信号的压缩采样不仅能降低数据量，还能缩短整个数据采集的时间。下面主要介绍这两类信号的压缩采样。

2.1.1 沿快变时间域的压缩采样

将压缩采样直接应用到通道数据上，Liebgott等人研究了不同稀疏基对通道数据重建效果[4]。通道数据的采集和重建流程如图1 所示。在该模型中，原始信号x 是通道信号，测量信号y 是x的随机抽样，即测量矩阵中每一行随机某一列为1，其他位置为0。压缩采样到测量信号后，通过凸优化算法恢复出原始信号的稀疏表达，然后通过稀疏反变换即可重建出原始通道信号。不同稀疏基对通道信号的重建误差随降采率的变化如图2 所示。从该图可以看出，降采倍数越高，重建效果越差。当选取波原子构造稀疏基时，重建效果最好，当丢弃80%的数据时，仍保持良好的重建效果，其次是傅里叶基，小波基最差。造成这种现象的原因是通道信号x 在波原子域的稀疏性最好。

上述采样是对通道信号的随机抽样。抽样是线性测量的一个特例，也更容易从模拟信号中得到。但随机抽样过程限制了测量矩阵的随机性。如何从模拟信号得到更通用的线性测量是模拟/信息转换的内容。Eldar 等人根据超声通道数据满足有限新息率（Finite Rate of Innovation, FRI）的特点，成功的将模拟/信息转换策略——Xampling 应用于超声通道数据的压缩采样和图像重建[5～7]。图3 是在实际机器上得到的结果。图3 (a)是正常奈奎斯特采样的结果，(b)和(c)是不同Xampling 采样测量下的结果，降采倍数分别为8倍和7 倍。关于Xampling 的更多内容可以参看[8,9]。

2.1.2 沿慢变时间域的压缩采样

沿慢变时间域的信号本身是离散的，所以其压缩采样不涉及复杂的模拟/信息转换。关键问题是如何进行压缩采样和重建。Quinsac 等人设计一系列对超声图像的空间采样策略，其中一种是对空间扫描线进行随机抽样[10,11]。超声图像的形成通常是通过对空扫描线的逐条扫描得到，这种对空间扫描线的随机抽样便实现了在慢变时间域的压缩采样。由于空间扫描线的随机抽样使得测量矩阵随机性不高，可能导致重建效果不好。为了解决这一问题，Quinsac 等人在重建时选择重建k 空间信号。这时，随机抽样得到的空间扫描线是k 空间信号的线性组合，从而提高重建效果。空间不同方向上的随机抽样重建结果如图4 所示。图(a)是不做随机抽样的结果，图(b)是在空间两个方向均做随机抽样的结果，图(c)和(d)分别是沿横向和纵向做随机抽样的结果。沿横向的随机抽样即是对空间扫描线的随机抽样，从图中可以看出，空间扫描线的随机抽样结果不如其他两种随机抽样。这是因为信号在横向的冗余度低比纵向低。对于冗余度更高的三维图像，这种采样策略更能发挥作用，从而提高三维超声成像的成像帧率[12]。

为了得到较好的重建效果，上述工作是在空间随机抽样，频域重建信号。清华大学的研究团队通过线性声场理论，证明了一次发射得到的平面波数据[13]是合成发射孔径(synthetic transmit aperture, STA)[14]得到数据的线性组合，提出基于压缩感知的合成发射孔径 (compressed sensing based synthetic transmit aperture, CS-STA)，从而通过改变发射方式实现了慢时间域的压缩采样[15,16]。该方法的压缩采样和重建均是在空域进行。由于该模式重建的是合成发射孔径图像，所以其保留了合成发射孔径高分辨率的特点。另外CS-STA每次发射所有阵元都被激活，所以相比传统合成发射孔径，它具有更高的对比度。图5 是该模式下的重建结果。其中Focused 是传统聚焦模式，它和合成发射孔径的成像帧频均为100Hz，CS64-STA 和CS32-STA 的成像帧频分别为200Hz 和400Hz。从图中结果来看，基于压缩感知的合成发射孔径不仅能提高帧频，还能保持高的空间分辨率和对比度。

图4. 不同空间采样策略的重建结果

图5. 基于压缩感知的合成发射孔径重建结果

2.2 超声逆散射问题

目前主流的超声成像是借助于阵元接收的后向散射信号。通过对后向散射信号进行延时叠加的波束合成算法即可确定待成像目标的位置及散射系数，从而形成超声图像。波束合成算法应用到了三个主要假设：声速在成像区域是固定且确定的，超声波束近似于射线直线传播以及传播过程没有多次散射[17]。因此，超声图像通常会有散斑、阴影、重影等伪像，严重影响图像质量。超声逆散射问题通过声场特性求解成像目标的声速、密度和吸收度等本质参数，从而提高图像质量。超声逆散射问题的求解应用比较成功的是超声CT (ultrasound computed tomography)。超声CT的采集方式和CT 类似，阵列也是环形阵列。借助于压缩感知，超声逆散射问题的求解也开始直接借助于非环形阵列。利用平面波一次发射接收到的后向散射信号，学者已在时域和频域建立了不同的求解模型。

2.2.1 频域模型

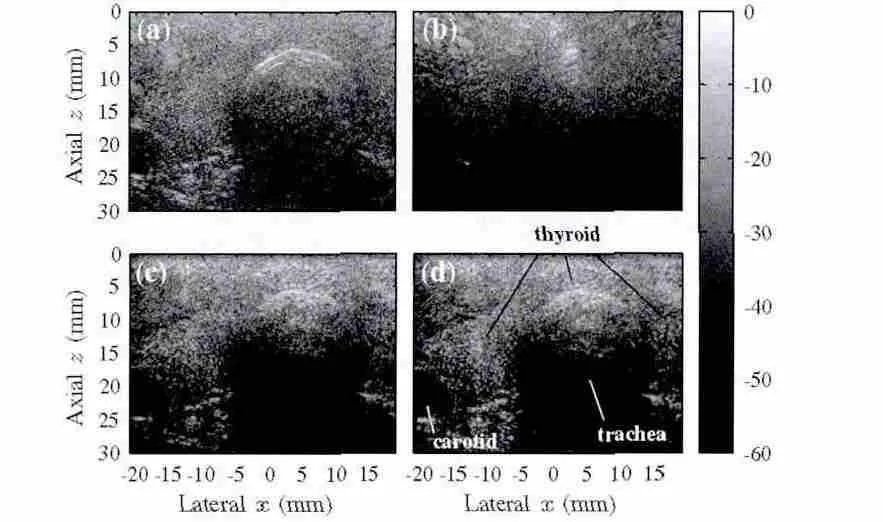
图6. 超声逆散射的频域求解

图7. SRBF 对仿真囊肿成像结果

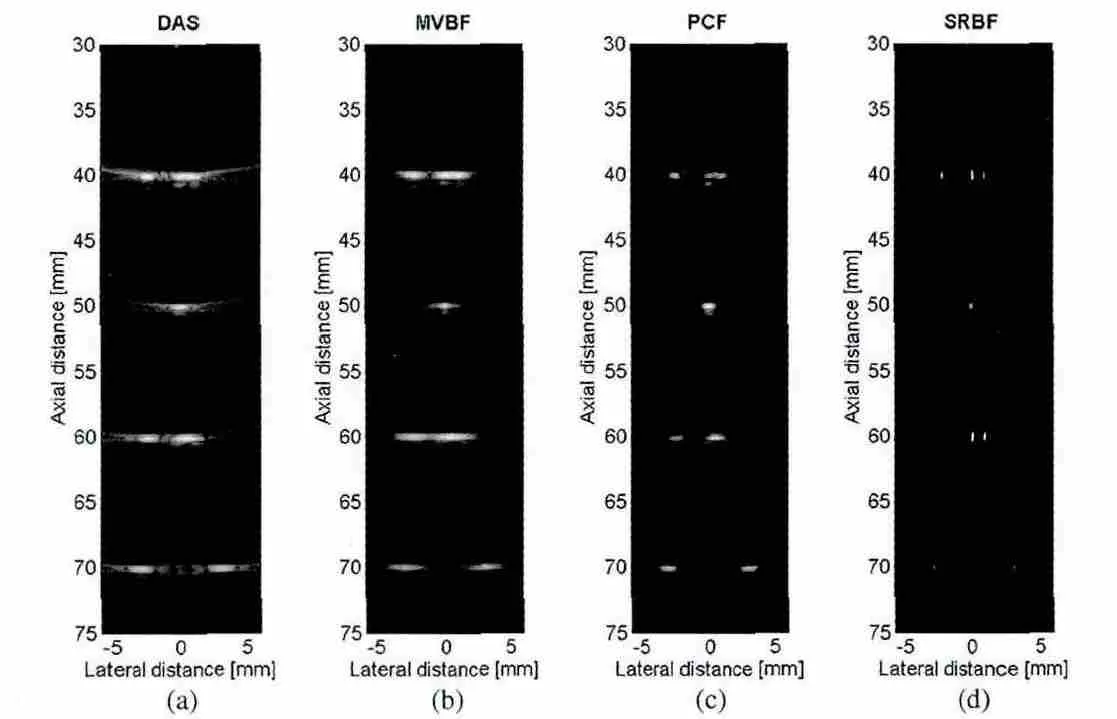
图8. SRBF 对仿真点目标的成像结果

假设成像目标的压缩率是稀疏的即稀疏基是单位矩阵，Schiffner 等人建立了压缩率与平面波回波信号的采样关系，其测量矩阵是根据波动方程在频域求取的格林函数。利用压缩感知算法即可重建出成像目标的压缩率[18]。只考虑压缩率这一成像参数可能会降低成像质量，多个成像参数的情况可以参见[19,20]，相关结果如图6 所示，图(a)和(b)分别是11 次发射的延时叠加算法和最小方差（minimum variance，MV）算法，图（c）和（d）是2 次发射的压缩感知逆散射算法。从该图可以看出，基于压缩感知的超声逆散射求解不仅发射次数少，对甲状腺的成像效果也更好。这一模型中测量矩阵通常非常大（180G 或450G），不能在通用计算机上实现，所以他们将其配置在图形处理器上（graphics processing unit，GPU）。同一小组还研究了快速多级算法（fast multipole method，FMM）对降低测量矩阵存储空间的能力[21]。

上述测量矩阵的确立是通过波动方程得到，借助超声系统的空间脉冲回波响应，Shen 等人在频域建立了成像目标的散射系数与平面波超声回波信号的采样关系[22]，利用压缩感知重建出成像目标的散射稀疏。该方法称为自适应稀疏表达波束合成（adaptive sparse representation beamformer, SRBF）如图7，8 所示，该方法得到的超声图像具有高的对比度和空间分辨率。

2.2.2 时域模型

除了频域求解，也可在时域构造散射系数与平面波超声回波信号的采样关系，利用压缩感知算法逆向求解散射系数[23～25]。虽然它们均是在时域求解，但不同的是测量矩阵的构造。根据延时构造的测量矩阵，由于矩阵中大量元素为0，所以方便存储[23]。利用超声系统的空间脉冲回波响应构造的测量矩阵数据量较大[25]，分布式压缩感知算法能适当降低数据量[24]。时域模型的求解也能表现高的空间分辨率和对比度，如图9 所示。

2.3 其他

除了上述基本超声成像，压缩感知在超声成像上还有很多其他的应用，如超声CT[26]，光声成像[27,28]和超声多普勒成像[29～31]。

2.4 展望

压缩感知在超声成像上的应用刚刚起步，目前研究的广度和深度都还远远不够。尽管目前的这些应用都良好地继承了压缩感知先天的优势，给超声成像这一领域带来新的机遇，但机遇与挑战并存，压缩感知是否能良好地移植到超声成像领域还需要更多的研究。

2.4.1 前景

压缩感知在超声上的应用前景主要表现在：（1）能够极大地降低原始信号的数据量（7～8 倍的降采），这对小型化超声系统如便携式和手持式超声系统非常有帮助。（2）在慢时间域的压缩采样和超声逆散射应用均能降低超声波发射次数，提高成像帧率。特别是超声逆散射应用，一次平面波发射即能重建高质量的超声图像从而实现超快速成像。高帧频的特点能极大地提高三维超声成像的实时性、剪切波弹性成像和心肌弹性成像的图像质量。

2.4.2 挑战

图9. 时域模型求解结果

上述应用前景能否实现主要存在如下挑战：（1）尽管应用模拟/信息转换的采样策略能在采样阶段即实现数据的压缩，但信号的重建相比传统的延时叠加算法更加复杂。如何降低信号重建过程的功耗又保持重建效果是压缩感知应用到实际小型化超声系统中的挑战，这就要求有更加效率的重建算法。（2）前述两种慢时间域的压缩采样虽然都能提高成像帧率，但也都面临不同的缺点。由于慢时间域信号冗余度低，直接空间扫描线的随机抽样使得重建效果差。基于压缩感知的合成孔径成像的图像重建是需要对各个接收通道和采样点重复重建过程，这使得整个重建过程非常耗时。（3）超声逆散射成像中，测量矩阵的通常很大。值得注意的是，这一问题已被时域模型的稀疏测量矩阵解决。但超声逆散射成像需要接受在体实验的检验。另外，因为超声逆散射图像的散斑特性和传统成像不一样，所以需要改变医生的看图习惯。

致谢：本文得到青年千人计划、国家自然科学基金优秀青年科学基金项目（61322101）及面上项目（61271131、81471665）资助。

[1] D. L. Donoho, "Compressed sensing," IEEE Transactions on Information Theory, vol. 52, pp. 1289-1306, 2006.

[2] M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, vol. 58, pp. 1182-1195, 2007.

[3] E. J. Candes and M. B. Wakin, "An introduction to compressive sampling," IEEE Transactions on Signal Processing, vol. 25, pp. 21-30, 2008.

[4] H. Liebgott, R. Prost, and D. Friboulet, "Pre-beamformed RF signal reconstruction in medical ultrasound using compressive sensing," Ultrasonics, vol. 53, pp. 525-533, 2013.

[5] T. Chernyakova and Y. Eldar, "Fourier-domain beamforming: the path to compressed ultrasound imaging," IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 61, pp. 1252-1267, 2014.

[6] N. Wagner, Y. C. Eldar, and Z. Friedman, "Compressed beamforming in ultrasound imaging," IEEE Transactions on Signal Processing, vol. 60, pp. 4643-4657, 2012.

[7] R. Tur, Y. C. Eldar, and Z. Friedman, "Innovation rate sampling of pulse streams with application to ultrasound imaging," IEEE Transactions on Signal Processing, vol. 59, pp. 1827-1842, 2011.

[8] M. Mishali, Y. C. Eldar, and A. J. Elron, "Xampling: signal acquisition and processing in union of subspaces," IEEE Transactions on Signal Processing, vol. 59, pp. 4719-4734, 2011.

[9] T. Michaeli and Y. C. Eldar, "Xampling at the rate of innovation," IEEE Transactions on Signal Processing, vol. 60, pp. 1121-1133, 2012.

文献[10]～[31]略。