金属柱壳膨胀断裂的实验与数值模拟*

任国武,郭昭亮,张世文,汤铁钢,金 山,胡海波

(1.中国工程物理研究院流体物理研究所,四川 绵阳 621999; 2.中国工程物理研究院,四川 绵阳 621999)



金属柱壳膨胀断裂的实验与数值模拟*

任国武1,郭昭亮1,张世文1,汤铁钢1,金 山1,胡海波2

(1.中国工程物理研究院流体物理研究所,四川 绵阳 621999; 2.中国工程物理研究院,四川 绵阳 621999)

基于一端起爆的柱壳外爆加载装置，采用多普勒速度测量仪(DPS)及高速分幅相机联合诊断柱壳的膨胀断裂过程。实验获得了壳体表面的速度历史和膨胀变形、裂纹萌生扩展到爆轰产物泄露的动态图像。利用光滑粒子流体动力学方法(SPH)开展了对应的数值模拟，计算结果与实验结果吻合较好。实验与数值模拟结果系统地给出了冲击波入射柱壳角、爆轰波稀疏角、内壁速度压力历史及壳体变形应变、壳体断裂等物理信息。

固体力学；断裂；DPS;SPH;柱壳；速度历史

爆轰加载下典型轴对称柱壳的膨胀断裂规律研究对指导武器工程结构设计有重要意义，尤其是壳体运动过程中发生的动态失效和破碎行为。由于工业及军事的需要，二战时期许多研究者对这一高应变率加载下的拉伸断裂问题产生了极大兴趣，研究主要集中于断裂物理机制、断裂应变、破片统计及力学行为研究，比如R.W.Gurney[1]通过经验分析方法估算了壳体的最终速度，G.I.Taylor[2]和R.H.Hoggatt等[3-4]给出了壳体的断裂判据。N.F.Mott[5]和D.E.Grady[6-7]分别从统计学及能量守恒观点出发系统地研究了壳体最终失效形成大量碎块的统计分布规律，建立动态破碎过程的理论描述，为该过程开展数值模拟奠定基础。

近年来，由于表征工具及光学测速仪的出现，通过实验获得了大量关于壳体膨胀断裂的物理信息[8-12]，比如微观结构特征,壳体的表面速度历史，从整体上提高了对金属壳体膨胀断裂过程的物理行为及微观机制的认识。然而对于这样一个与加载应变率、柱壳构型以及材料本身微观缺陷有关的复杂过程，这些研究工作还不足以建立有效的物理模型以开展相应数值模拟研究[13-14]。

本文中基于从一端起爆的柱壳加载实验装置，利用多普勒速度测量仪(DPS)、高速分幅照相分别得到壳体膨胀表面速度历史和表面变形断裂特征。为避免基于网格算法的有限元方法在模拟材料断裂时须删除一定数量的失效单元，采用光滑粒子流体动力学方法(SPH)模拟该过程。

1 实验设计及测试

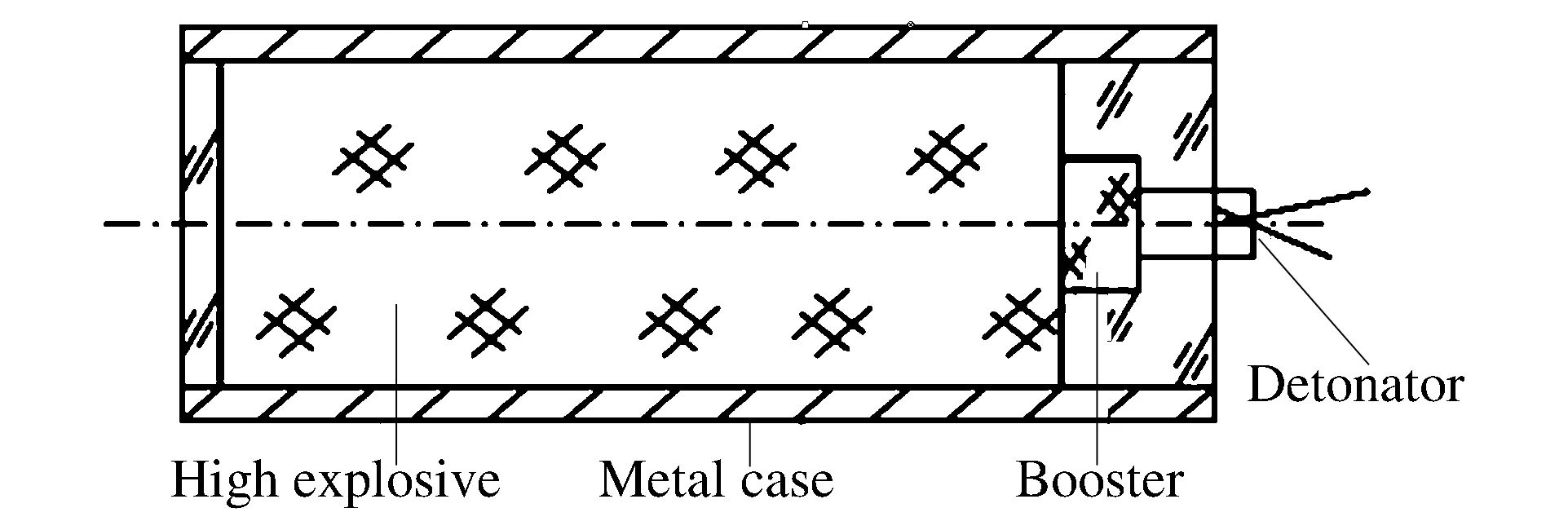
图1 内装炸药的金属柱壳装置示意图Fig.1 Schematic diagram of metal casemounted with high explosive

金属柱壳爆轰加载下装置示意图如图1所示。装置为内装炸药的金属柱壳，柱壳两端为有机玻璃塞，装置采用一端起爆。在此加载下，柱壳的径向膨胀可近似满足一维平面应变条件，应力三维度为0.577。实验中柱壳材料为一种含碳量约0.45%的45钢，微观结构包含铁素体和珠光体2种晶粒。本实验中所用的45钢未做任何热处理。柱壳的外直径48 mm、壁厚4 mm、长140 mm。装置内的主装炸药为JOB-9003，直径40 mm、长120 mm。

实验中采用的测试技术有转镜式分幅相机和DPS测速仪。转镜式分幅相机主要用于拍摄壳体表面的膨胀断裂过程。为获得柱壳表面清晰图像，实验采用白色背景的前照明分幅照相，照明光源为炸药激发氩气袋分别从两个角度照亮柱壳；白色背景采用白纱布，距离照相物体约20 cm，由此可清楚地衬出柱壳的轮廓。转镜式高速分幅相机的转速为240 kr/min，对应的幅频间距为0.5 μs。在柱壳边界放置一时标雷管记录柱壳膨胀过程分幅图像的精确起始时刻。DPS的测试探头置于柱壳表面的中部，测量该位置处的径向速度随时间的变化。

2 数值模拟

为深入了解柱壳膨胀断裂过程的运动规律，采用动力学有限元程序Autodyn6.1数值模拟等尺寸的实验模型。Lagrange网格、SPH粒子分别代表炸药和45钢。炸药与金属柱壳间的相互作用通过该软件的间隙接触算法来实现。为方便计算，模拟的模型去掉传爆药和雷管套，考虑柱壳装置的对称性，只取四分之一模型进行计算。用Mie-Grüneisen状态方程和Johnson-Cook强度模型来描述45钢。Mie-Grüneisen方程表示为：

(1)

式中：pH和EH为Hugoniot曲线上点的压力和内能，γ为Grüneisen系数。

冲击波速度us和粒子速度up的关系为：

us=c0+Seup

(2)

式中：c0为等熵下的声速，Se为us-up曲线的斜率。45钢的状态方程参数为：ρ=7.85 g/cm3,剪切模量76.7 GPa,屈服强度496 MPa,c0=4.57 km/s,Se=1.49,γ=2.17。

45钢的本构方程用Johnson-Cook强度模型描述，表示为：

(3)

式(3)中参数的意义见文献[15],参数值为：A=496 MPa,B=434 MPa,n=0.307,C=0.008 4,m=0.804,Tr=1 765 K。

炸药为JOB-9003，采用JWL状态方程来描述，其压力形式为:

(4)

状态参数为：ρ=1.85 g/cm3,D=8.71 km/s,pCJ=34.4 GPa,A=824.83 GPa,B=7.06 MPa,R1=4.327 3,R2=0.792,ω=0.28。

3 结果分析及讨论

3.1 表面速度历史

实验采用DPS测量的壳体表面速度历史如图2所示，整体上表现为初始冲击波到达边界时速度迅速上升到一个极大值，之后由于冲击波在柱壳内外壁的多次反射，速度发生来回振荡，幅值有一定的下降。但炸药的持续做功导致壳体膨胀速度最终达到1.7 km/s，此时壳体膨胀断裂过程趋于一个稳定状态。从图2中可以得到第1个速度峰值为0.996 km/s，加载应变率约为4.15×105s-1。在速度趋于稳定前，可清楚地发现其周期性振荡5个回合，时间间隔约为1.5 μs，由此估算出45钢的冲击波速度大约为5.3 km/s。根据冲击波与爆轰波在界面上视速度相等的关系[16]，即Dc=Dsinα，其中D为炸药爆轰波速，Dc为柱壳中的冲击波速，由此计算出壳内冲击波的入射角α=37.48°。

图2 壳体表面速度及位移实验与数值模拟比较Fig.2 Comparison of experimental and numerical comparisons of expansion velocity and displacement

从图2可以看出，数值模拟结果与实验结果吻合较好。然而在速度上升沿部分，模拟结果没有实测结果陡峭，最终自由膨胀阶段高于实验结果。通过对速度的积分获得壳体膨胀位移x，即x=R-R0，R0为初始柱壳的外径，实验结果与模拟结果吻合非常好。在图中壳体膨胀变形的持续时间为16.2 μs，最大位移值x=24.4 mm，相对于初始半径R0=24 mm，膨胀变形ε(=x/R0)为1.016 7。事实上此时壳体表面已有大量纵向裂纹产生，这在接下来的分幅相机结果中可以看出。

速度与位移的实验与数值模拟结果比较从侧面反映了：(1)壳体表面的位移信息量没有速度历史丰富；(2)采用数值模拟时尽管位移与实验符合非常好，但速度历史上不一定对应得好，尤其是初始阶段冲击波在沿壁厚方向来回反射造成的速度振荡以及壁间可能发生的层裂行为。这对材料强度模型及所含的物理过程建模提出了更高的要求。

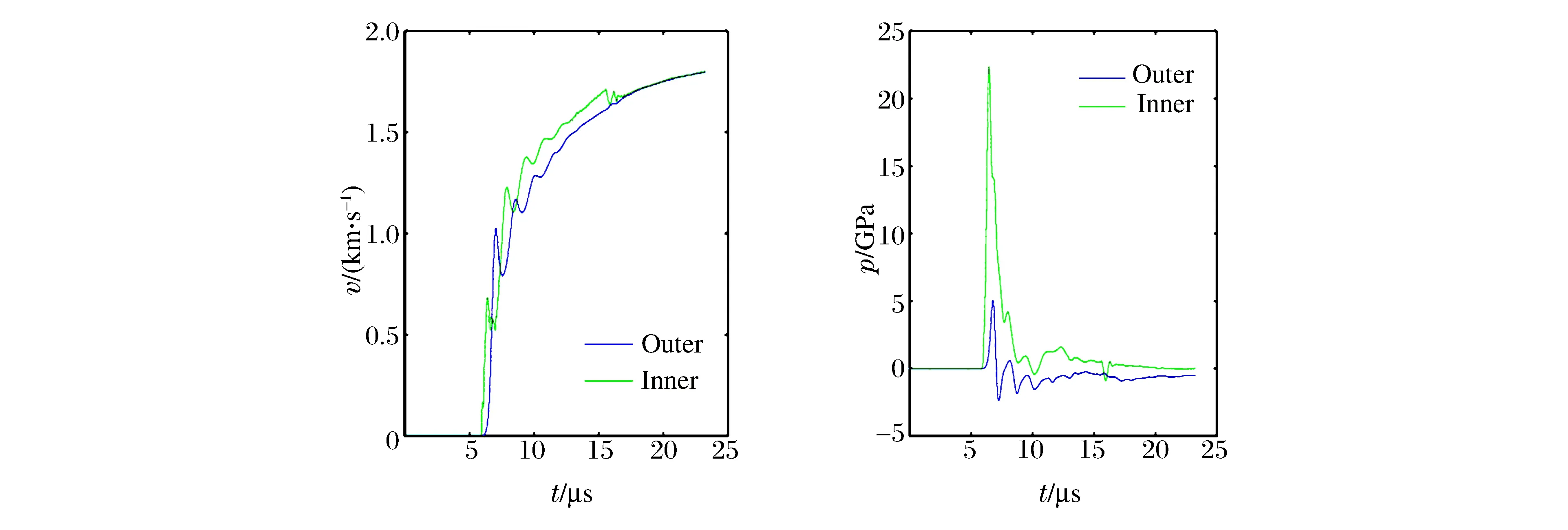
图3 柱壳内壁和外壁的速度及压力历史Fig.3 Velocity and pressure histories for inner and outer walls of cylindrical shell

图4 柱壳的压力分布Fig.4 Pressure distributions within the cylinder

图3是基于数值模拟给出的柱壳内外壁的速度和压力历史。由于实验上无法获得柱壳内壁的历史，因此只有通过数值模拟展示，以更清楚地看出炸药对壳体内壁做功带来的速度响应。初始爆轰阶段，壳体内壁的速度是大于外壁的，并且由于壁内冲击波的传播，外壁的速度极小值刚好对应于内壁的极大值。随着时间的推移，壳体内外壁的速度趋于一致。图3中同时展示了内外壁的压力历史。正压力表示为压缩，负为拉伸。内壁初始阶段一直为压缩状态，炸药加载下压力迅速达到最大值(约23 GPa)，而外壁的压力历史只有大约5 GPa。而后，外壁一直处于拉伸状态，而内壁则处于压缩状态，这与Taylor的物理分析是一致的。

图4给出了炸药和柱壳的压力分布，最大压力为37.09 GPa；炸药的CJ爆压为34.4 GPa。由于模型采用的是一端起爆，所以爆轰波前沿是中心突出，不同于平面透镜获得垂直于柱体轴向的爆轰波。这个结果是和文献[9]采用CALE程序模拟平面波透镜加载柱壳的结果类似的。同时计算了柱壳内冲击波前沿与垂直于壁厚方向的夹角，为52.81°，与之前理论推算的结果是一致的。炸药与金属界面发射出的稀疏波与垂直于壁厚方向的夹角为49.56°。

3.2 表面光学分幅图像

图5展示了高速分幅相机记录的壳体在不同时刻的膨胀变形、裂纹萌生及产物泄露。柱壳的底角放置一时标雷管用于标定分幅图像的时刻。为了便于定量分析及讨论，事先在柱壳表面做了沿环向的标记线，从距起爆端15 mm开始(对应于主炸药顶部位置)，离底部5 mm、间隔为20 mm，共7条。选取从柱壳顶端沿下某标记线为参考来计算不同时刻此位置的工程变形应变，定义为：

(5)

式中：R0为初始柱壳外壳直径，为48 mm；R为壳体膨胀后的直径。

图5 光学分幅图像记录了壳体表面不同时刻的局域变形、裂纹萌生扩展及产物泄露Fig.5 Optical framing camera records of local deformation, crack initiation, propagation anddetonation product leakage of cylindrical shell surface

由公式(5)计算了图5中壳体第2条标记线处(距离顶端为35 mm)的工程形变ε，分别为：0.149、0.331、0.660 、1.117。图5(a)～(d)分别对应壳体表面发生局域变形、大量裂纹萌生、扩展及产物泄露。从图5(c)可以看出，尽管表面出现大量裂纹，但未发现爆轰产物泄露，意味着壳体内部处于压缩或滑移接触状态，但由于诊断技术不足,无法判断此时保持接触的厚度是多少。从图5(d)发现的产物泄露表明该位置有较明显的缺陷存在，壳体最早萌生裂纹及扩展最快的地方也在于此(从图5(c)可以看出)。通过工程应变的定义，产物泄露时ε=1.117，意味着此时壳体已变形到初始外径的一倍。基于壳体表面裂纹扩展的观察，其表面的失效模式是拉伸型的，不同于早期在钛合金柱壳实验中观察到的以剪切滑移为主。因此可判断该实验中45钢柱壳的失效断裂模式为拉-剪混合型，即表面为拉伸、内部为剪切。

由于基于网格算法的有限元在模拟壳体断裂时，需要删除一定数量的单元，造成了整体壳体一些断裂特征不能精确体现。为此，采用了SPH算法来模拟壳体断裂以避免上述问题。同时，由于材料初始微观缺陷的存在带来其不均匀性，这些缺陷将是裂纹和材料失效的萌生点，我们采用了Autodyn使用的Mott分布描述。Mott提出了一个依赖应变ε的失效函数h(ε)，假设在单位长度的柱壳内应变从ε到ε+dε发生断裂的概率为h(ε)dε，并建议h(ε)=Aeγε，意味着h(ε)随应变会迅速上升。因而，当应变从ε到ε+dε时，柱壳发生失效的概率为：

(6)

当h(ε)为幂指数形式时，获得的统计分布为Weibull分布。

图6 数值模拟的柱壳膨胀断裂过程Fig.6 Simulation results of cylindrical shell from initial deformation to crack growth

数值模拟中采用的是公式(6)的分布形式，其中ε=0.307为45钢的断裂应变，γ=16.0。图6展示了柱壳膨胀裂纹扩展过程的模拟结果。图6(a)给出了柱壳外表面的整体变形状态，同时发现在壳体顶端，由于边界稀疏波效应，出现了沿环向的层状碎片。随着柱壳进一步往外运动，环向拉伸作用力超过金属的断裂强度导致微裂纹萌生，如图6(b)所示。 图6(c)展示了壳体表面形成了不同宽度的裂纹，且沿纵向已扩展了一定距离以及贯穿了壁厚方向，结果与图5(d)是一致的。图6(d)～(f)是与(a)～(c)对应同时刻的壳体厚度变化图。

4 结 论

开展了内置炸药加载柱壳的实验研究，利用DPS及高速分幅相机联合诊断了金属柱壳的膨胀断裂过程。DPS用于测量壳体表面膨胀的速度历史，获得了壳体膨胀过程中柱壳在爆轰加载下丰富的信息量。高速分幅相机拍摄了壳体膨胀过程的表面形貌信息，获得壳体表面从不稳定发展、裂纹萌生扩展到贯穿、产物泄漏的过程。利用SPH方法，建立了对应的壳体模型，通过速度历史及壳体膨胀断裂的数值与实验比较，获得了一致的结果。利用数值模拟还获得了实验无法测量的物理信息，比如内壁的压力、速度历史及爆轰波稀疏角，这对于深入分析壳体膨胀断裂过程有着重要的参考价值。

[1] Gurnery R W. The initial velocity of fragment from bombs, shells and grenades[R]. Army Ballistic Research Laboratory Report No. 405, 1943.

[2] Taylor G I. Analysis of the explosion of a long cylindrical bomb detonated at one end[M]∥Scientific Papers of G. I. Taylor, vol. III. Cambridge: Cambridge University Press, 1963,30:277-286.

[3] Hoggatt R H, Recht R F. Fracture behavior of tubular bombs[J]. Journal of Applied Physics, 1968,93(3):1856-1862.

[4] Singh M, Suneja H R, Bola M S, et al. Dynamic tensile deformation and fracture of metal cylinders at high strain rates[J]. International Journal of Impact Engineering, 2002,27(9):939-954.

[5] Mott N F. Fragmentation of shell cases[J]. Proceedings of Royal Society of London, Series A, 1947,43(2):300-308.

[6] Grady D E. Fragmentation of rings and shells: The legacy of N. F. Mott[M]. New York: Springer, 2006.

[7] Grady D E, Olsen M L. A statistics and energy based theory of dynamic fragmentation[J]. International Journal of Impact Engineering, 2003,29(10):293-306.

[8] Martineau R L, Anderson C A, Smith F W. Expansion of cylindrical shells subjected to internal explosive detonations[J]. Experimental Mechanics, 2000,40(2):219-225.

[9] Goto D M, Becker R, Orzechowski T J, et al. Investigation of the fracture and fragmenation of explosively driven rings and cylinders[J]. International Journal of Impact Engineering, 2008,35(12):1547-1556.

[10] 胡八一,董庆东,韩长生,等.TC4钛合金及40Cr钢破片中绝热剪切的TEM分析[J].高压物理学报,1996,10(1):37-43. Hu Ba-yi, Dong Qing-dong, Han Chang-sheng, et al. TEM observation of shear bands in Ti-6Al-4V and 6140 steel[J]. Chinese Journal of High Pressure Physics, 1996,10(1):37-43.

[11] 汤铁钢,谷岩,李庆忠,等.爆轰加载下金属柱壳膨胀破裂过程研究[J].爆炸与冲击,2003,23(6):529-533. Tang Tie-gang, Gu Yan, Li Qing-zhong, et al. Expanding fracture of steel cylinder shell by detonation driving[J]. Explosion and Shock Waves, 2003,23(6):529-533.

[12] 胡海波,汤铁钢,胡八一,等.金属柱壳在爆炸加载断裂下的单旋现象[J].爆炸与冲击,2004,24(2):97-107. Hu Hai-bo, Tang Tie-gang, Hu Ba-yi, et al. An study of uniform shear bands orientation selection tendency on explosively loaded cylindrical shells[J]. Explosion and Shock Waves, 2004,24(2):97-107.

[13] 谭成文,王富耻,李树奎,等.内爆炸加载条件下圆筒的膨胀、破裂规律研究[J].爆炸与冲击,2003,23(4):305-308. Tan Cheng-wen, Wang Fu-chi, Li Shu-kui, et al. Deformation and fracture of cylindrical tube under inside explosive loading[J]. Explosion and Shock Waves, 2003,23(4):305-308.

[14] 王新征,张松林,邹广平.内部短药柱爆炸作用下钢筒破裂特征的数值分析[J].高压物理学报,2010,24(1):61-66. Wang Xin-zheng, Zhang Song-lin, Zou Guang-ping. Numerical analysis on fragmentation properties of the steel cylinder subjected to detonation of internal short cylindrical explosive charge[J]. Chinese Journal of High Pressure Physics, 2010,24(1):61-66.

[15] 胡昌明,贺红亮,胡时胜.45号钢的动态力学性能研究[J].爆炸与冲击,2003,23(2):188-192. Hu Chang-ming, He Hong-liang, Hu Shi-sheng. A study on dynamic mechanical behavior of 45 steel[J]. Explosion and Shock Waves, 2003,23(2):188-192.

[16] 经福谦.实验物态方程导引[M].2版.北京:科学出版社,1999.

(责任编辑 曾月蓉)

Experiment and numerical simulation on expansion deformation and fracture of cylindrical shell

Ren Guo-wu1, Guo Zhao-liang1, Zhang Shi-wen1, Tang Tie-gang1, Jin Shan1, Hu Hai-bo2

(1.InstituteofFluidPhysics,ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China; 2.ChinaAcademyofEngineeringPhysics,Mianyang621999,Sichuan,China)

Relying on the explosively driven setting of one-end detonator initiation and using the Doppler velocimetry and high-speed framing camera, we diagnosed the expansion and fracture process of the cylindrical shell. The results obtained from our experiment provide the velocity-time history of the shell surface and its dynamic snapshots referring to expansion deformation, crack initiation and propagation, and explosion product leakage. The results from the SPH simulation are in reasonably good agreement with the experimental findings. Systemic analysis of experiments and simulations determine incident angle of shock wave for cylindrical shell, releasing angle of explosion wave, velocity and pressure profile of internal wall and deformed strain, fracture process of cylindrical shell.

solid mechanics; fracture; DPS; SPH; cylindrical shell; velocity profile

10.11883/1001-1455(2015)06-0895-06

2013-09-12；

2015-02-10

国家自然科学基金项目(11172279); 中国工程物理研究院科学技术发展基金重点项目(2012A0201011)

任国武(1981— )，男，博士,助理研究员,gwren@fudan.edu.cn。

O346.1 国标学科代码： 13015

A