自适应底座附加冲击载荷的积分表达和影响因子*

仲健林，任 杰，蔡德咏，胡建国,3

(1.南京理工大学机械工程学院，江苏 南京 210094；2.72465部队，山东 济南 250022；3.西安现代控制技术研究所，陕西 西安 710065)



自适应底座附加冲击载荷的积分表达和影响因子*

仲健林1，任 杰1，蔡德咏2，胡建国1,3

(1.南京理工大学机械工程学院，江苏 南京 210094；2.72465部队，山东 济南 250022；3.西安现代控制技术研究所，陕西 西安 710065)

为研究附加冲击载荷的解析方法和影响因子，推导了附加冲击载荷的积分表达式，获得了影响附加冲击载荷的3个主要参数；建立底座的数值模型，并通过实验验证了数值模型建立方法的正确性。在数值模型基础上，结合MISO(multiple-input, single-output)多元广义多项式神经网络方法，建立了底座力学特性数学模型，对附加冲击载荷的影响因子进行智能决策分析。分析结果表明：对于附加冲击载荷的影响因子由高到低排序为帘线模量、截面面积、帘线间距，且当相应参数的变化导致附加冲击载荷增大时，该参数对附加冲击载荷的影响因子逐渐减小。

爆炸力学；影响因子；数值模型；自适应底座；附加冲击载荷

导弹悬垂弹射技术具有发射准备时间短和利于实现任意点随机发射等优点，常见弹射方式有压缩空气式、燃气式、燃气-蒸汽式等[1-4]。悬垂弹射冲击瞬间产生几十吨至几百吨的弹射后坐力，为减小弹射冲击后坐力对发射车的影响以及实现任意点随机发射，对悬垂弹射平台采用了自适应底座技术。附加冲击载荷是自适应底座最主要的力学性能指标之一，涉及发射平台动力匹配、动态响应特性等重要问题。目前，中国对自适应底座的研究才刚起步，尚未建立反映其结构形式与附加冲击载荷之间内在规律的解析方法，对附加冲击载荷的影响因子也未进行深入研究，较多的是通过实验手段来检验自适应底座的工作特性[5]，因此对附加冲击载荷解析方法和影响因子进行研究，能够有效地推动导弹悬垂弹射技术的发展。为研究自适应底座附加冲击载荷的解析方法和影响因子，首先，建立自适应底座的数学模型，取自适应底座壁面微元推导附加冲击载荷积分表达式；其次，建立实验状态自适应底座数值模型，通过实验验证数值建模方法的正确性，对比附加冲击载荷峰值的数值模型解和解析解，验证附加冲击载荷解析方法的正确性；最后，对自适应底座进行参数化数值分析，建立其神经网络数学模型，针对帘线模量、截面面积、帘线间距参数，对附加冲击载荷的影响因子进行智能决策分析。

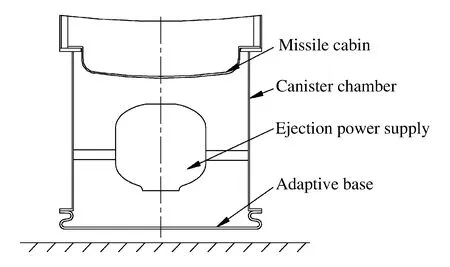
图1 悬垂弹射系统 Fig.1 Drape ejection system

1 附加冲击载荷解析方法

1.1 悬垂弹射系统

如图1所示，导弹悬垂弹射系统主要包括导弹尾罩、弹射动力源、初容室和自适应底座。自适应底座是由帘线/橡胶复合材料经多层粘接热压而成的柔性构件。悬垂弹射时，自适应底座沿垂向和径向发生膨胀，与路面接触后能够自动适应不同的路面状态，大幅降低弹射系统对发射场坪的要求。

悬垂弹射系统起竖完成后，自适应底座悬离地面一定高度。弹射时，弹射动力源产生高压气体，在初容室内部形成高压；压力作用在导弹尾罩上为导弹弹射提供动力，作用在自适应底座上则会使底座产生膨胀变形，触地后将压力释放至地面。由于底座悬垂，作用在底座上的气体压力不能全部传递到地面上。通过实验发现，底座对初容室底部形成了冲击载荷作用，称之为附加冲击载荷。

1.2 附加冲击载荷的积分表达

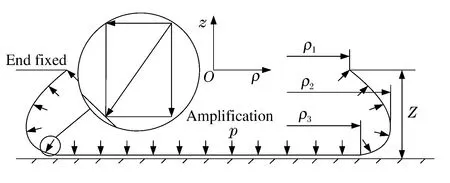
图2 膨胀状态自适应底座示意图Fig.2 Diagrammatic sketch of adaptive base in expansion state

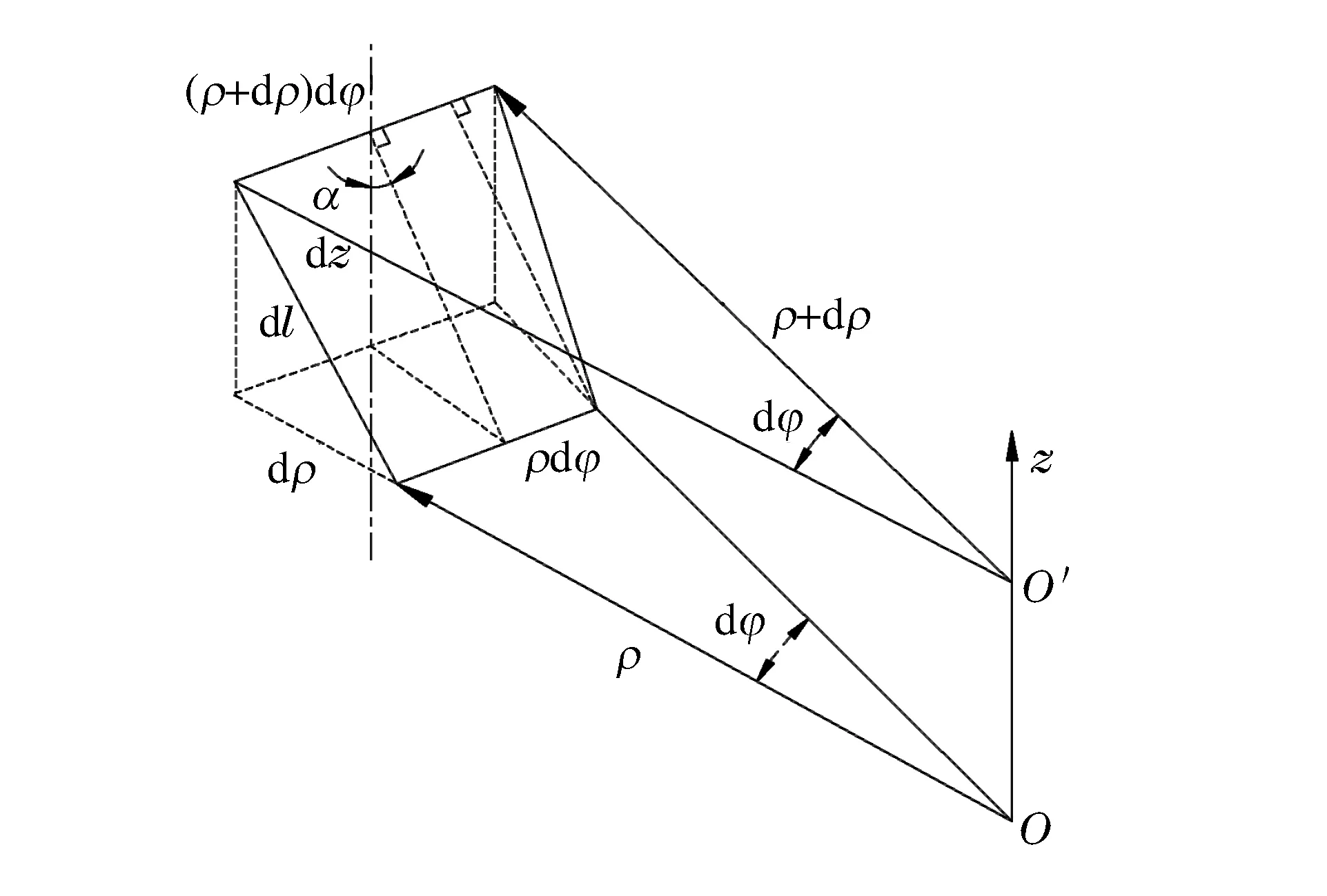
图3 柱坐标系中的dAFig.3 dA in the cylindrical coordinate system

导弹弹射冲击瞬间，高压气体充入自适应底座内部，底座外部为标准大气，内外压强均作用在底座壁面上。底座壁面很薄，研究时忽略壁面厚度，将其受力状态简化为只受内部相对压强p(实际内压与大气压强差值)的作用。在压强p的作用下，自适应底座发生膨胀变形，最后与地面接触，释放压力达到平衡状态，如图2所示。

在柱坐标系下对膨胀状态的自适应底座进行研究，如图2所示，建立柱坐标系(ρ,φ,z)，坐标系原点O取在底座上端面中心处，z向垂直向上。ρ1为底座上端面在水平面上投影的矢径，ρ2为底座壁面最外缘到z轴的距离，ρ3为底座触地边缘到z轴的距离，底座触地边缘与上端面的距离为Z。在矢径为ρ3的区域上，内部压力与地面反作用力相互平衡，作用在该区域上的内部压力不产生附加冲击载荷。将自适应底座壁面压力沿底座的径向和垂向进行分解，如图2所示，压力p的径向分量使底座承受径向张力作用，垂向分量产生附加冲击载荷。

膨胀后的底座壁面为曲面，在曲面上取微元dA进行研究，dA在柱坐标系(ρ,φ,z)中如图3所示。

压强p作用在dA微元上，压力为dP=pdA，dP的垂向分量dF即为附加冲击载荷，dF表示为:

dF=dPsinα=pdAsinα

(1)

式中:α为dA微元与z轴的夹角。

微元dA可视为梯形，其高是dρ/sinα，忽略二阶小量，则微元的面积可近似表示为:

(2)

式中:dφ为dA微元在柱坐标系中对应的角度。

由式(1)和式(2)，dA区域上dP的垂向分量:

dF=dPsinα=pdAsinα=pρdρdφ

(3)

如图2所示，底座膨胀后的壁面为光滑曲面。设光滑曲面为Σ，引入矢径为ρ2的辅助平面Σ3。Σ3将光滑曲面Σ分为Σ1和Σ2。Σ1、Σ2与任一平行于z轴的直线交点只有一个，则Σ1和Σ2的方程为单值函数z=z(ρ,φ)。Σ1和Σ2在与z轴垂直的水平面上投影区域分别为D1和D2。函数z=z(ρ,φ)在D上具有连续偏导数，被积函数f(ρ,φ,z)在光滑曲面Σ上连续。首先将曲面投影到水平地面上，将对面积的曲面积分化为积分区域上的二重积分。

式(3)为dA曲面微元的附加冲击载荷微分表达式，对自适应底座的壁面进行积分即可得到附加冲击载荷的积分表达式。根据曲面积分的算法，有：

(4)

式(4)为附加冲击载荷的积分表达式，是变上下限积分，ρ1和ρ3均为变量。本文所研究底座处于水平状态，ρ1为底座上端面在水平地面上投影的矢径，即底座上端面的内径；ρ3与底座触地区域形状和大小有关，底座触地区域为圆形，ρ3为圆的半径，见图4。因此，积分表达式(4)的上下限有定值，式(4)可改写为:

(5)

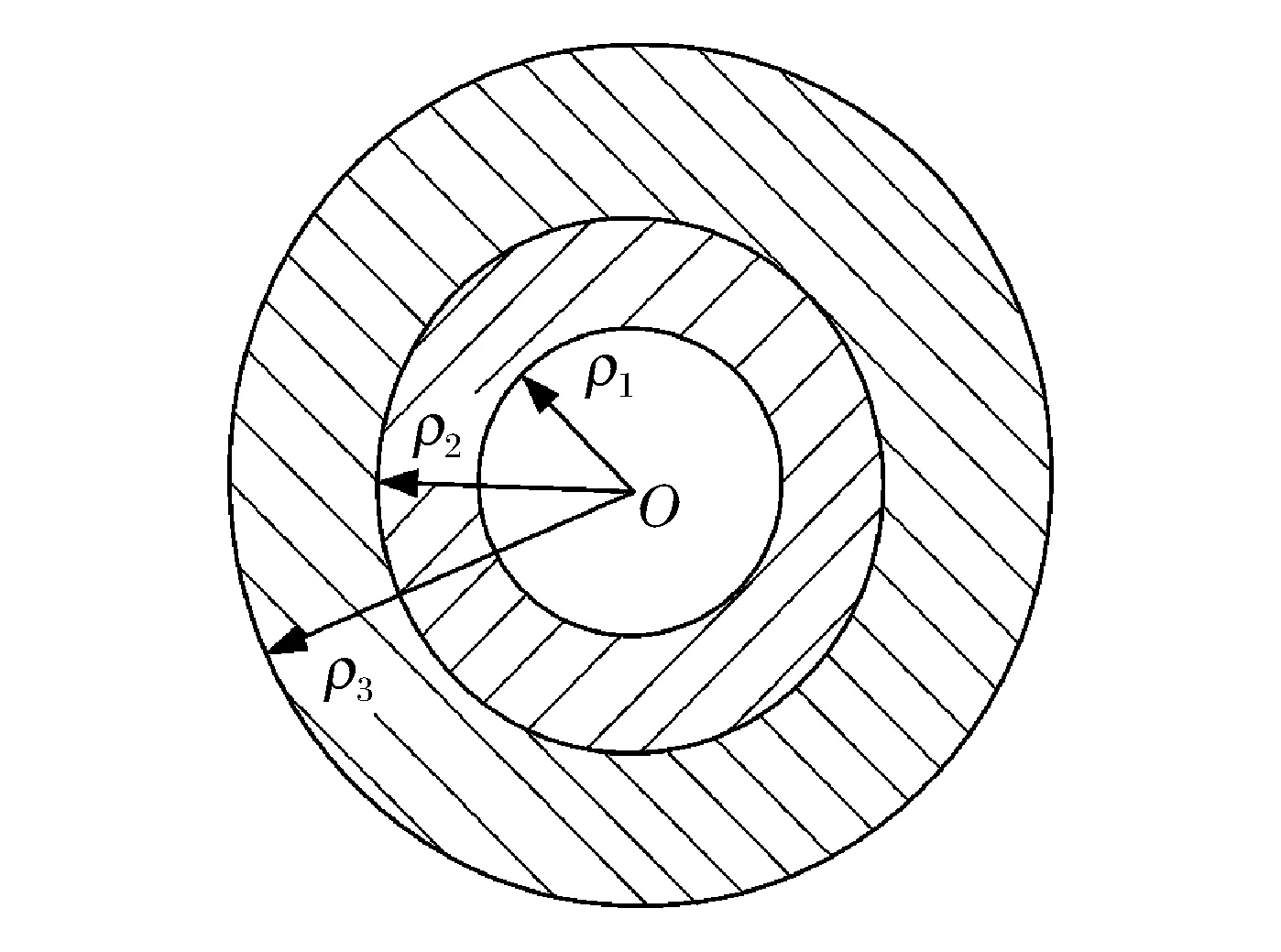
图4 积分区域的水平地面投影Fig.4 Horizontal ground projection of integration region

为便于描述，将矢径ρ1包含的区域的水平投影面积设为S，矢径ρ3包含的区域的水平投影的面积设为S′，可将式(5)改写为:

(6)

式(6)即为附加冲击载荷的理论计算公式，可用来计算底座在悬垂弹射时所产生的附加冲击载荷。由式(6)可知，附加冲击载荷与底座的触地面积直接相关，对于既定结构和特定压强下的底座，其触地面积主要取决于帘线-橡胶复合材料的材料特性。由模量混合律可知，帘线/橡胶复合材料的模量由组分材料的模量和体积含量所决定[6]。由于橡胶的模量和帘线的模量相差甚远，橡胶的模量对复合材料模量的贡献很小，因此，底座附加冲击载荷影响因子的主要参数为：帘线模量、帘线截面面积、帘线间距。

2 自适应底座数值模型

建立底座的数值模型，搭建实验平台测量底座产生的附加冲击载荷，验证数值模型的正确性。改变底座中帘线模量，模拟获得不同帘线模量下的数值模型的附加冲击载荷，与积分表达式的计算结果进行对比，验证附加冲击载荷积分表达式推导的正确性。

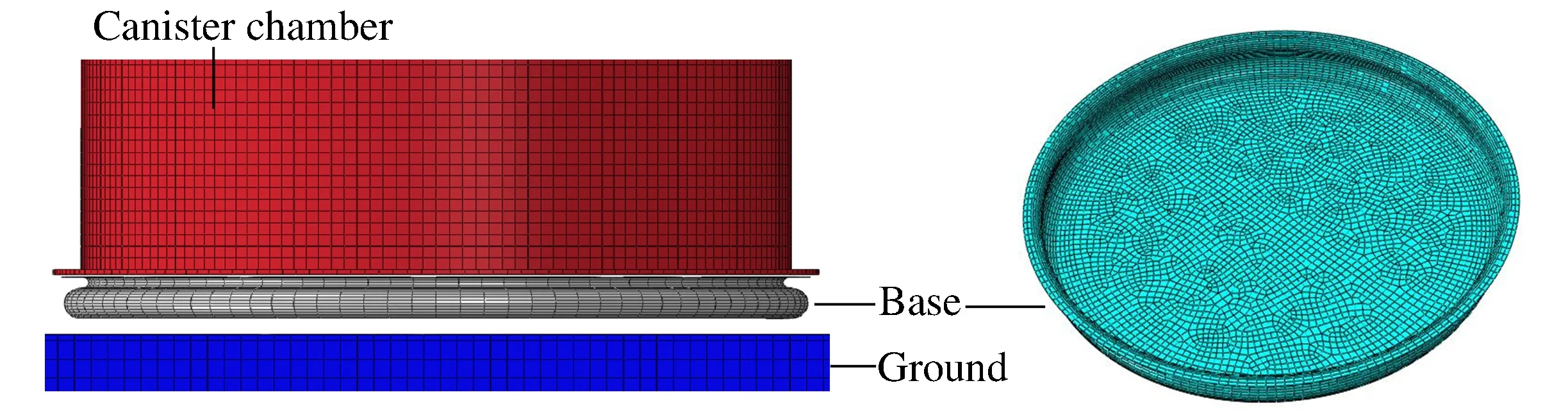
图5 自适应底座数值模型Fig.5 The numerical model for the adaptive base

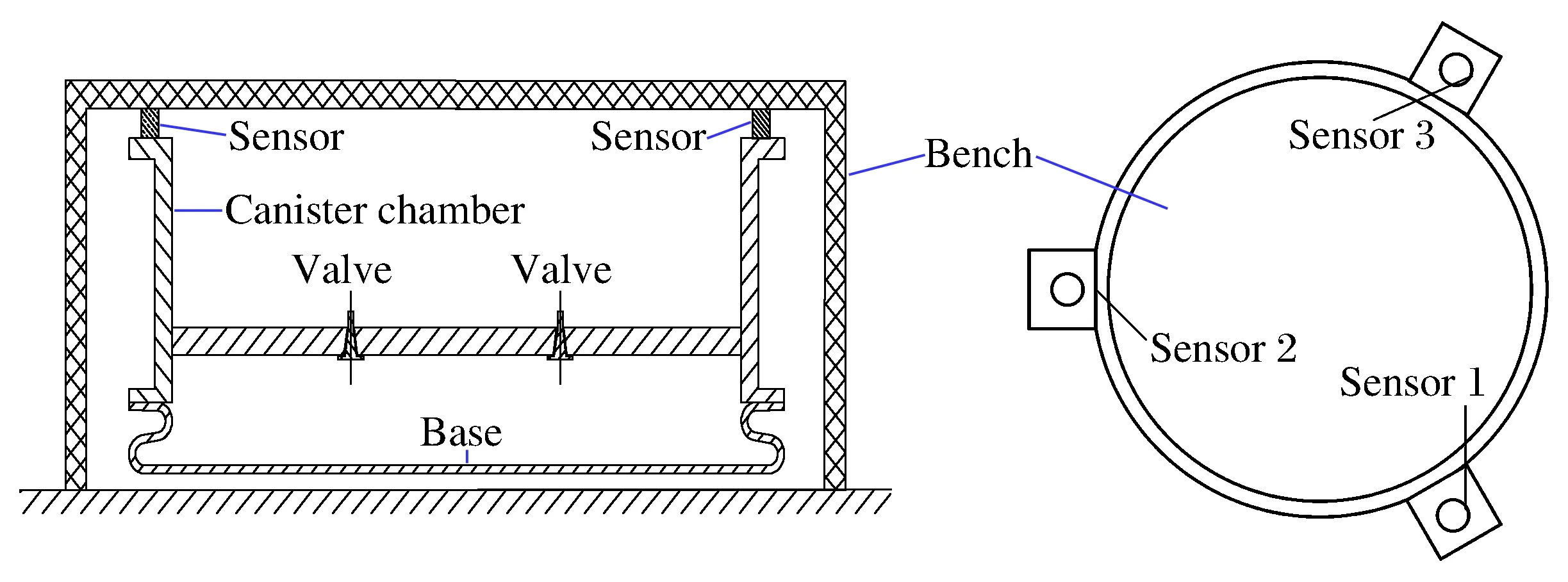
图6 实验平台示意图Fig.6 Schematic diagram of the experimental platform

2.1 数值模型与实验验证

引用刘琥等[5]的方法，建立实验状态下自适应底座的数值模型，采用S4R单元对底座结构进行离散，采用Rebar单元模拟帘线增强相，通过Rebar单元的横截面面积来定义帘线的直径d，帘线角θ按所在层的具体位置取值；采用Mooney-Rivilin本构模型模拟橡胶材料，初容室和地面分别赋予相应的材料属性。在数值模型中定义自适应底座上端面和初容室底部固连，在初容室与自适应底座的连接界面上提取附加冲击载荷作用力，在自适应底座底面与地面之间建立接触关系，自适应底座数值模型见图5。

如图6所示，附加冲击载荷测量实验平台由底座、初容室、测力传感器、支撑台架等部件构成。通过进气阀在底座内部进行加压，底座膨胀与地面接触后对初容室产生附加冲击载荷。附加冲击载荷通过初容室上端面传递至支撑台架，利用周向均布的3个测力传感器测量初容室上端面与支撑台架之间的作用力，附加冲击载荷值远大于初容室的自身重力，因此该作用力可视为附加冲击载荷。

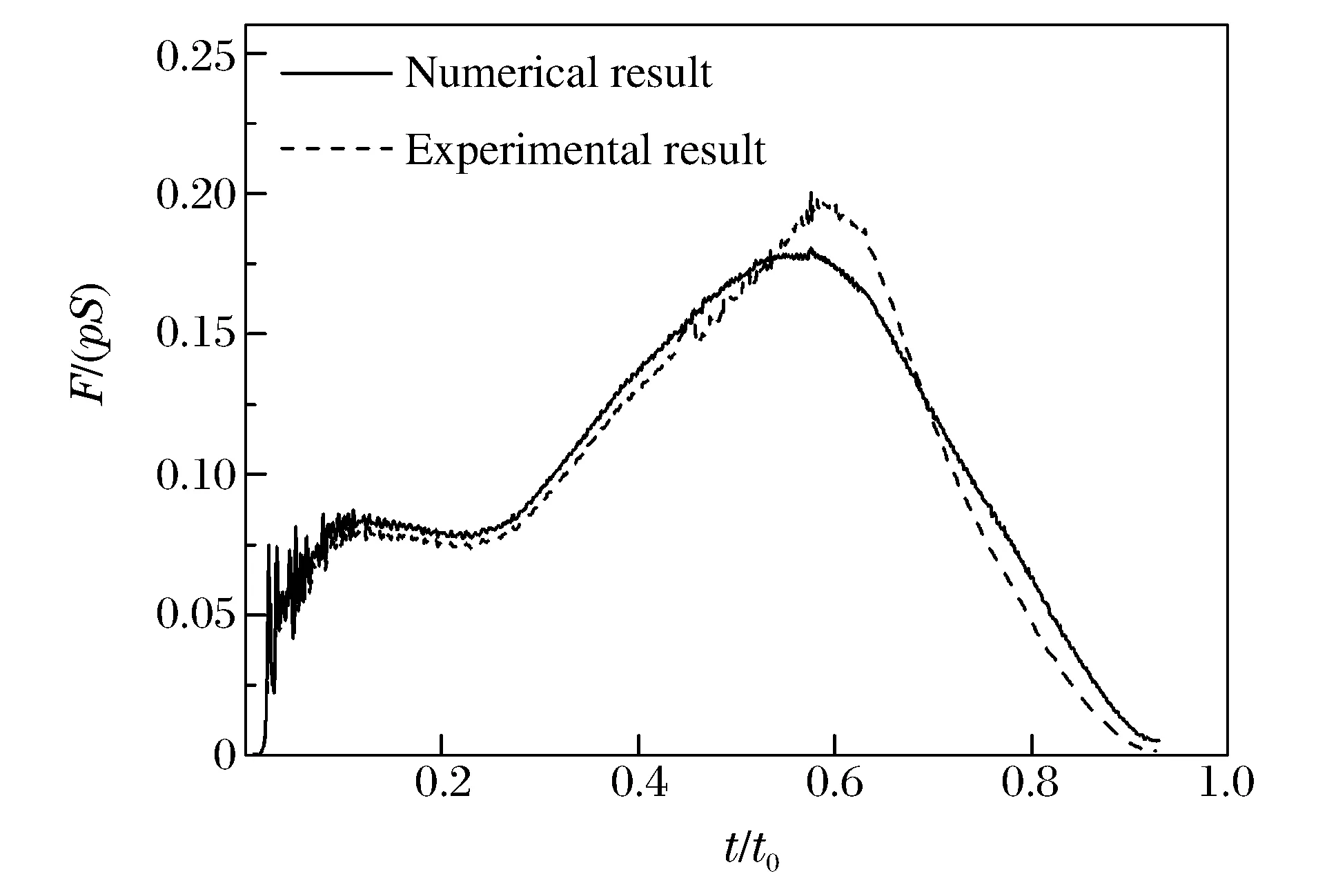
图7 附加冲击载荷对比Fig.7 Comparison of additional impact load

针对实验模型，将3个测点的作用力曲线叠加得到附加冲击载荷曲线，在数值模型中，提取自适应底座对初容室的作用力，此作用力即为附加冲击载荷。对计算结果进行量纲一化处理，将附加冲击载荷除以内部压强峰值p与底座上端面的面积S的乘积，图7给出了附加冲击载荷随量纲一时间变化曲线。数值模型解与实验测量值变化规律一致，附加冲击载荷峰值的相对误差约为7%，满足工程精度要求，验证了数值建模方法的正确性。

2.2 积分表达式的数值模型验证

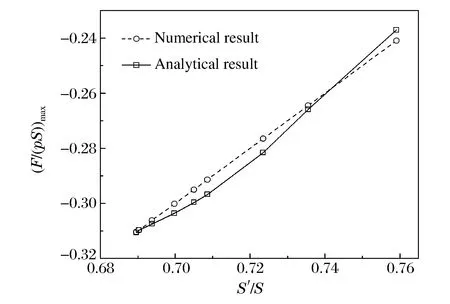
图8 附加冲击载荷峰值的解析解与数值解Fig.8 Numerical solutions and analytical solutions of the maximum additional impact load

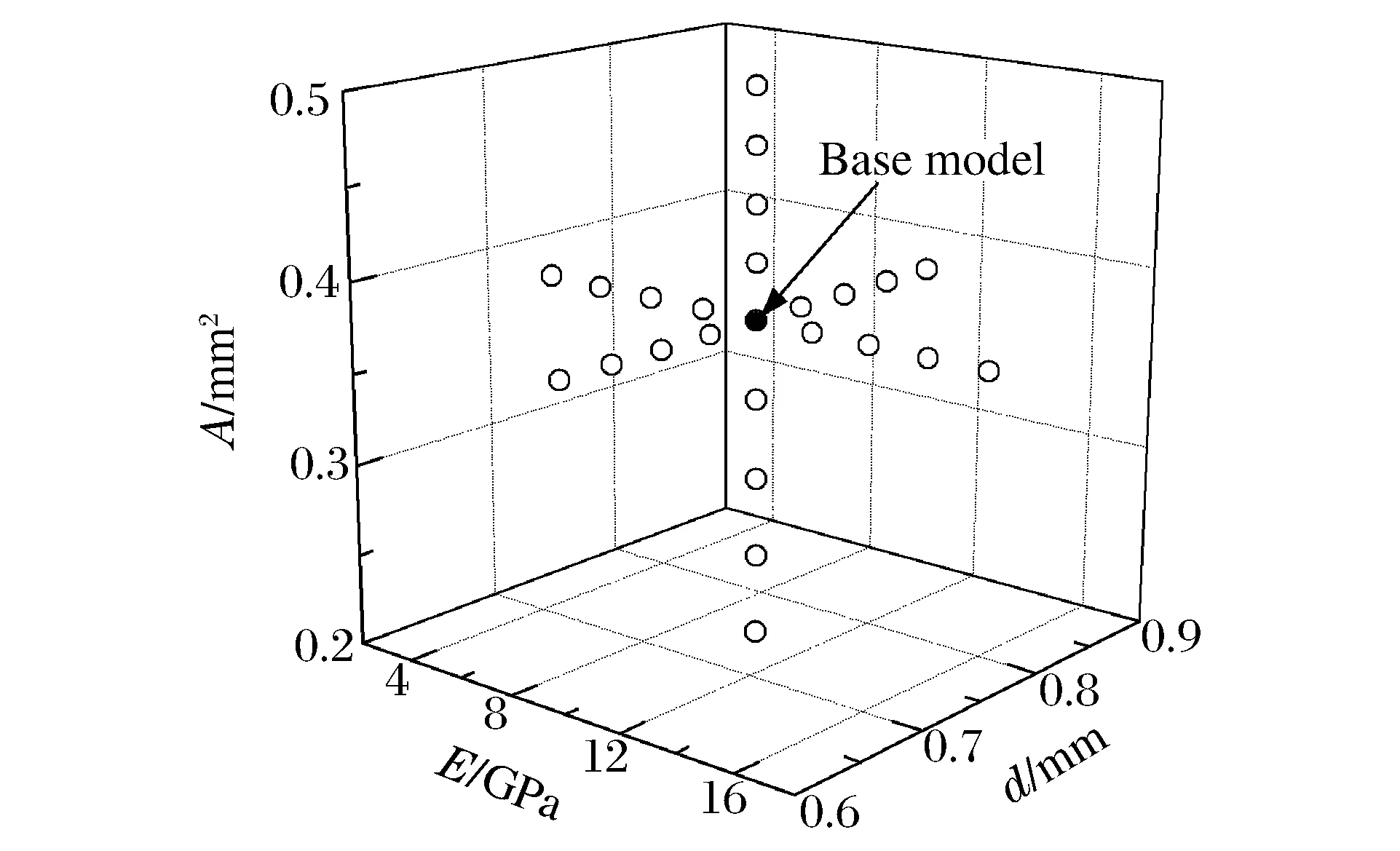
图9 参数化数值模型输入参数Fig.9 Input parameters of the parametric numerical model

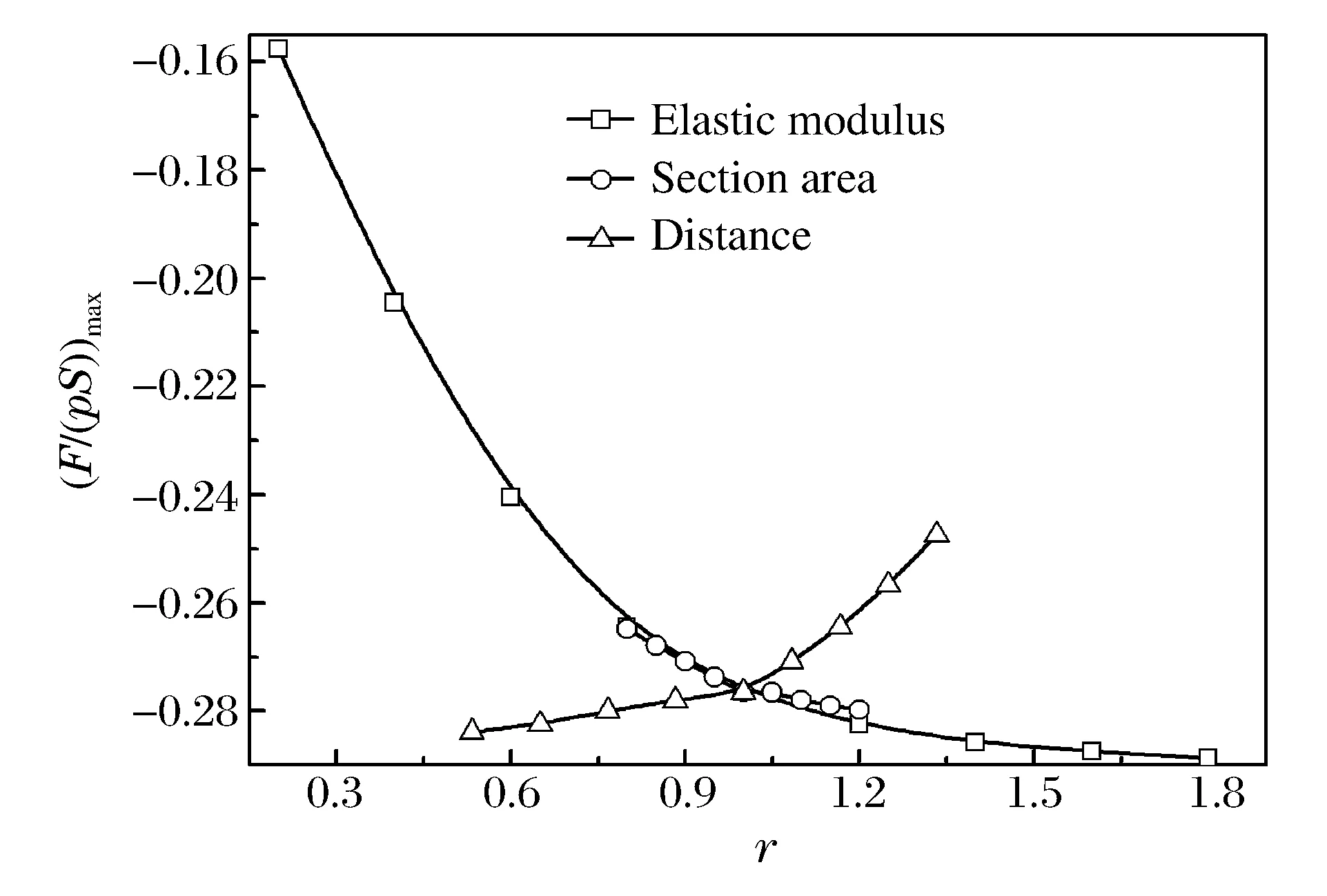
图10 参数化数值模型输出参数Fig.10 Output parameters of the parametric numerical model

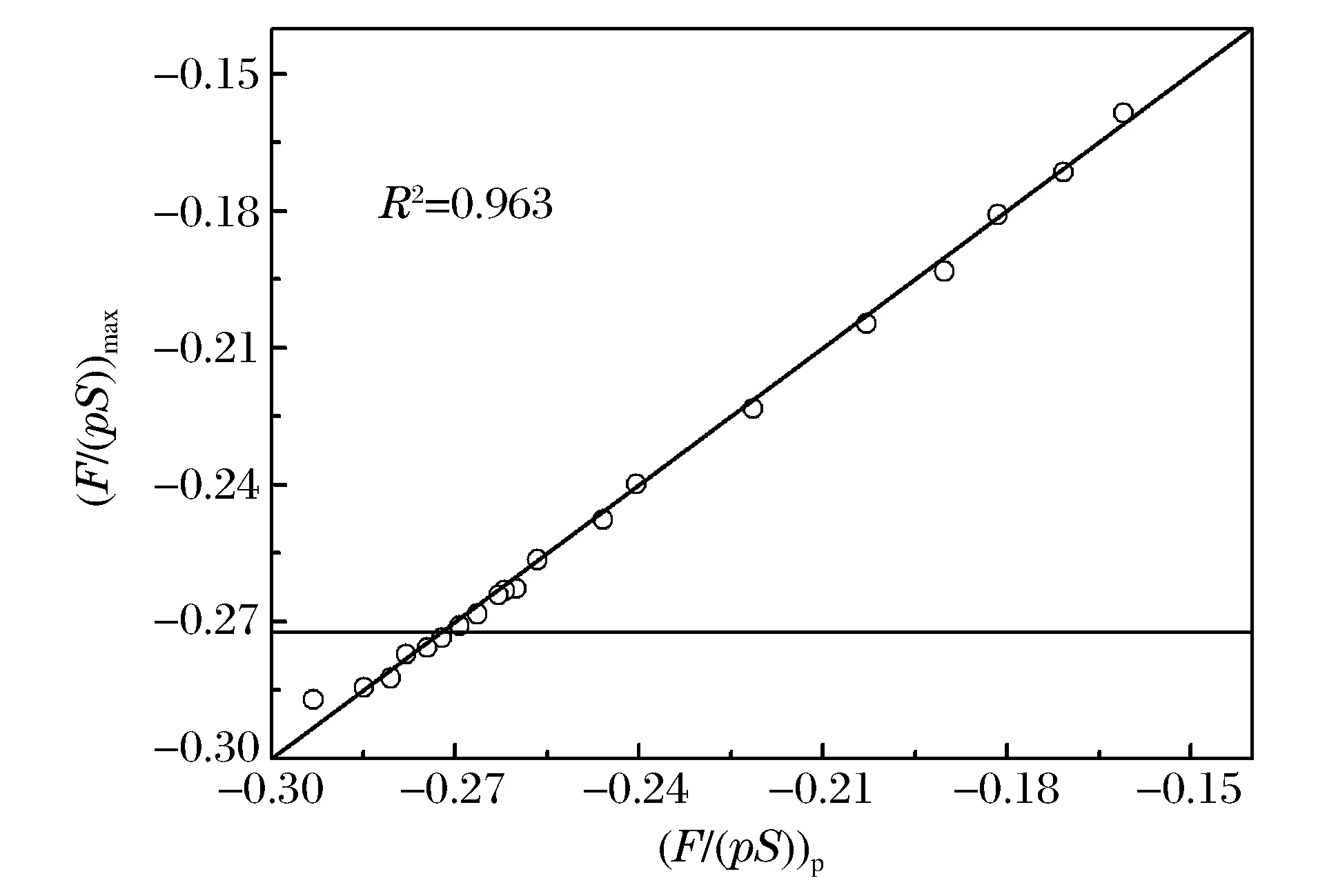
图11 数学模型误差分析Fig.11 Error analysis of mathematic model

在2.1节中数值模型的基础上，通过改变帘线弹性模量形成材料特性不同的数值模型。不同的弹性模量所对应的底座变形程度不一致，触地面积也不相同，帘线弹性模量分别取0.7、0.8、1.0、2.0、2.5、3.0、3.5、4.0和5.0 GPa。

对于一个既定结构的自适应底座，p和S均已知，S′可以通过实验测得，也可通过模拟获取。S′从模拟结果中获取，代入式(6)可得到附加冲击载荷的解析解；数值解则由有限元软件对节点积分后得到。将计算结果进行量纲一化处理，取S′/S为横坐标，分别取量纲一化后的附加冲击载荷峰值解析解与数值解为纵坐标，绘制成曲线，见图8。由图8可知，附加冲击载荷峰值为负，表示附加冲击载荷的方向向下；附加冲击载荷峰值的解析解与数值解基本一致，附加冲击载荷解析公式的推导是正确的。

3 帘线组分的影响因子分析

3.1 自适应底座参数化数值分析

在底座数值模型中，应用Rebar单元模拟帘线，帘线截面面积由Rebar单元的横截面积定义，帘线的间距由Rebar单元的间距定义[7]。结合Python语言，实现了底座的参数化数值分析，为影响因子的智能决策提供输入和输出数据，具体步骤为:(1)建立自适应底座的基准数值模型；(2)实现帘线模量、截面面积、帘线间距的参数化设定；(3)完成自适应底座的参数化数值计算，输出附加冲击载荷计算结果。对基准模型中帘线模量E、截面面积A、帘线间距d进行参数化设定，经过排列、组合、筛选后规划出27组参数化数值模型输入参数，如图9所示。

对以上参数化的数值模型进行模拟计算，得到参数化数值模型的输出参数(附加冲击载荷峰值(F/(pS)max)，取帘线模量、截面面积、间距与基准模型中相应参数的比值r为横坐标，量纲一化的附加冲击载荷峰值为纵坐标，绘制成曲线，如图10所示。由图10可知，随帘线模量、截面面积增大，附加冲击载荷峰值(方向向下)增大；随着帘线间距增大，附加冲击载荷峰值(方向向下)减小。这是由于帘线模量、截面面积的增大会导致底座刚度增大，附加冲击载荷最大瞬间，底座的触地面积减小，由式(6)可知，附加冲击载荷峰值增大；对于帘线间距增大导致的附加冲击载荷峰值减小，原因类似，不再赘述。附加冲击载荷峰值的变化规律与基于附加冲击载荷解析方法的理论分析结论相符。

3.2 影响因子智能决策分析

以参数化数值模型分析的输入和输出参数为样本，基于多元函数逼近理论的MISO多元广义多项式神经网络方法，编写程序，训练获得自适应底座力学性能数学模型[8-10]。随机选取20组数值计算样本(F/(pS)max与自适应底座力学性能数学模型的计算结果(F/(pS))p进行对比，如图11所示，数学模型预测值的方差R2=0.963，表明了自适应底座力学性能数学模型的准确性[11]。

当自适应底座力学性能数学模型训练完成后，在基准模型的基础上，针对帘线模量、截面面积、间距，按照一定比例，改变相应参数的值，代入数学模型进行计算，观察附加冲击载荷峰值相对于基准峰值的变化。可以在该参数的变化范围内取多组值来进行数学模型计算，最终分析出该参数对附加冲击载荷峰值的影响程度。在相对于基准值[-50%～50%]的区间内，对帘线模量、截面面积、帘线间距以5%比例递增进行取值γ，给出相应的量纲一附加冲击载荷峰值随帘线模量、截面面积、帘线间距变化的值(F/(pS))E、(F/(pS))A、(F/(pS))d见表1。

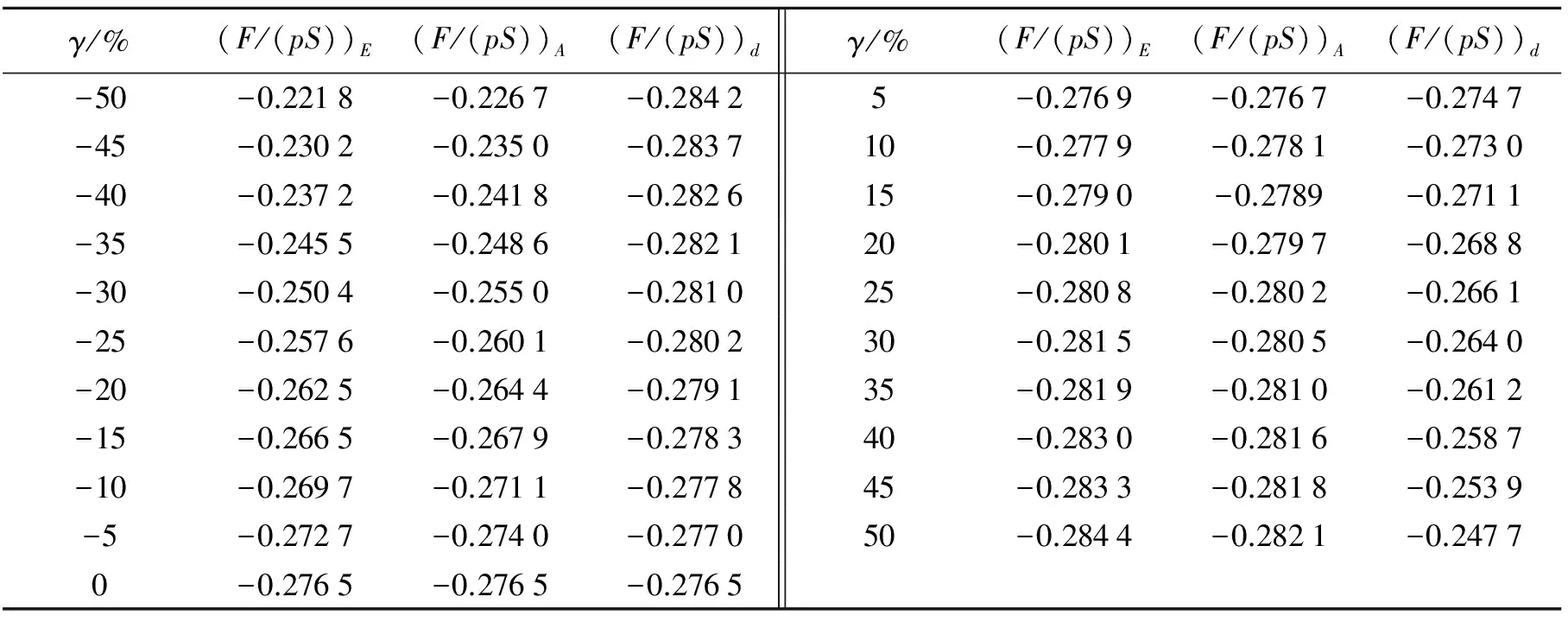
表1 附加冲击载荷峰值计算结果Table 1 The calculation results of the peak additional impact load

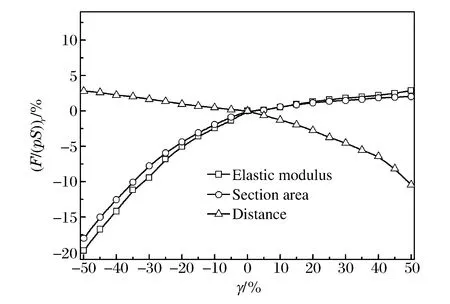
图12 附加冲击载荷峰值变化比例曲线Fig.12 Change ratio of the peak additional impact load

取帘线模量、截面面积、帘线间距的变化比例为横坐标，附加冲击载荷峰值相对于基准值的变化比例为纵坐标，绘制成曲线，见图12。定义影响因子为n=ΔηF/Δη，其中ΔηF表示某一区间上附加冲击载荷峰值变化比例的差值，Δη表示相应参数在该区间上的变化比例的差值。由图12中曲线斜率可知，随着弹性模量和截面面积变化比例的增加，这2个参数对附加冲击载荷的影响因子减小；整个比例变化区间上，相对于帘线截面面积，帘线模量对附加冲击载荷峰值的影响因子较大。随着帘线间距变化比例的增大，该参数对附加冲击载荷峰值的影响因子增大。帘线弹性模量和截面面积增大，底座刚度增加，触地面积减小，由附加冲击载荷解析方法可知，附加冲击载荷峰值增大，同样地，帘线间距增大则附加冲击载荷峰值减小，因此，当相应参数的变化会导致附加冲击载荷峰值增大时，则该参数对附加冲击载荷峰值的影响因子逐渐减小，反之亦成立。帘线模量、截面面积和帘线间距对于附加冲击载荷峰值的影响因子依次减小。

4 结 论

对自适应底座的附加冲击载荷的产生机理和影响因子进行了研究。推导了自适应底座附加冲击载荷的积分表达式；基于MISO多元广义多项式神经网络方法，建立了其力学特性数学模型，对附加冲击载荷的影响因子进行了智能决策分析。得到了以下结论：

(1)附加冲击载荷峰值的数值模型解和实验测得值相对误差约为7%，文中关于自适应底座数值模型的建立方法是正确的。

(2)附加冲击载荷峰值的解析解与数值模型解基本一致，验证了附加冲击载荷解析方法的准确性，可用于计算自适应底座在悬垂弹射时产生的附加冲击载荷；即定结构和特定压强下的自适应底座，其附加冲击载荷的影响因子的主要参数为帘线模量、截面面积、帘线间距。

(3)帘线模量、截面面积、帘线间距3个参数对附加冲击载荷的影响因子依次减小，相应参数的变化会导致附加冲击载荷峰值增大时，则该参数对附加冲击载荷峰值的影响因子逐渐减小。

本文研究方法和结论能够为自适应底座的结构优化和综合性能预测评估提供技术支撑。

[1] Spearman M L. Innovation in aerodynamic design features of Soviet missiles[R]. NASA 20080014230, 2008.

[2] 杨风波,马大为,杨帆.高压弹射装置内弹道建模与计算[J].兵工学报,2013,34(5):527-534. Yang Feng-bo, Ma Da-wei, Yang Fan. Interior ballistics modeling and calculation of high-pressure ejection device[J]. Acta Armamentarii, 2013,34(5):527- 534.

[3] 毕世华,王汉平.导弹垂直弹射过程中制动锥度动力学特性研究[J].北京理工大学学报,2004,24(9):762-765. Bi Shi-hua, Wang Han-ping. A study on the dynamical characteristics of the braking cylindrical shells during the vertical ejection of missiles[J]. Transaction of Beijing Institute of Technology, 2004,24(9):762-765.

[4] 张仁军,鲍福延.两种不同注水方式的燃气蒸汽式发射系统内弹道性能比较[J].固体火箭技术,2005,28(1):5-9. Zhang Ren-jun, Bao Fu-yan. Comparison of internal ballistic properties between gas and steam launching system in two different modes of water injection[J]. Journal of Solid Rocket Technology, 2005,28(1):5-9.

[5] 刘琥,倪晓琛,白静.自适应底座悬垂弹射过程附加冲击载荷分析[J].导弹与航天运载技术,2012(3):23-25. Liu Hu, Ni Xiao-chen, Bai Jing. Additional impact load study during the drape launch of adapting base[J]. Missiles and Space Vehicles, 2012(3):23-25.

[6] 沈观林.复合材料力学[M].北京:清华大学出版社,2007:127-128.

[7] Ren Jie, Zhong Jian-lin, Ma Da-wei. A method of cord-rubber composite materials based on cord tensile modulus correction[C]∥2013 International Forum on Special Equipments and Engineering Mechanics. 2013:248-252.

[8] Erdogan H, Gulal E. Identification of dynamic systems using Multiple Input-Single Output (MISO) models[J]. Nonlinear Analysis: Real World Applications, 2009,10(2):1183-1196.

[9] 段宝福,张猛,李俊猛,等.逐孔起爆震动参数预报的BP神经网络模型[J].爆炸与冲击,2010,30(4):401-406. Duan Bao-fu, Zhang Meng, Li Jun-meng, et al. A BP neural network model for forecasting of vibration parameters from hole-by-hole detonation[J]. Explosion and Shock Waves, 2010,30(4):401-406.

[10] Abdelkader M, Tarek G, Kais B. Reduced complexity Volterra model of non-linear MISO system[J]. International Journal of Modelling, Identification and Control, 2012,16(2):134-148.

[11] 郭亚娟,孟光.基于近似模型的空调配管阻尼优化设计[J].振动与冲击,2013,32(6):185-189,194. Guo Ya-juan, Meng Guang. Optimization design of pipe's damping layers in air conditioner based on approximation model[J]. Journal of Vibration and Shock, 2013,32(6):185-189,194.

(责任编辑 张凌云)

Integral expression and affecting factors for the additional impact load of an adaptive base

Zhong Jian-lin1, Ren Jie1, Cai De-yong2, Hu Jian-guo1,3

(1.SchoolofMechanicalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China; 2. 72465Army,Jinan25002,Shandong,China; 3.Xi’anModernControlTechnologyResearchInstitute,Xi’an710065,Shaanxi,China)

To research the analytical method and affecting factors of the additional impact load, an integral expression formula was derived for the additional impact load. Three major parameters affecting the additional impact load were obtained. A numerical model was built for the adaptive base. And the correctness of this modeling method was verified by the test. Based on the built numerical model, a mathematic model was developed by combining the MISO (multiple-input, single-output) multivariate generalized polynomials neural network to describe the mechanical properties of the adaptive base. Thereby, the intelligent decision analysis was conducted for the affecting factors of the additional impact load. The analysis results show that the affecting factors for the additional impact load from high to low levels are cord modulus, section area and cord spacing. If the change of one parameter would cause the additional load to increase, the affecting factor by the corresponding parameter on the additional impact load decreases.

mechanics of explosion; affecting factor; numerical model; adaptive base; additional impact load

10.11883/1001-1455(2015)05-0668-07

2014-03-19；

2014-05-12

国家自然科学基金项目(51303081);江苏省自然科学基金项目(BK20130761)

仲健林(1988— )，男，博士研究生; 通讯作者： 任 杰,renjie@njust.edu.cn。

O381 国标学科代码： 13035

A