可变容积附加气室空气悬架的参数优化与控制*
2015-04-12李仲兴琚龙玉黄定师
李仲兴,琚龙玉,江 洪,黄定师
(1.江苏大学汽车工程与交通学院,镇江 212013; 2.江苏大学机械工程学院,镇江 212013; 3.博世汽车部件有限公司,苏州 215000)
2015162
可变容积附加气室空气悬架的参数优化与控制*
李仲兴1,琚龙玉1,江 洪2,黄定师3
(1.江苏大学汽车工程与交通学院,镇江 212013; 2.江苏大学机械工程学院,镇江 212013; 3.博世汽车部件有限公司,苏州 215000)
基于热力学与车辆动力学理论,建立了带可调容积附加气室空气悬架的数学模型;以提高车辆行驶平顺性、轮胎接地性和操纵稳定性为目标,附加气室容积与减振器阻尼系数为设计变量,建立附加气室空气悬架的多目标优化模型;接着采用线性加权和法,将多目标优化问题转化为单目标优化问题;最后整合车辆典型工况下的优化结果,以载荷、车速及路面等级为控制输入量,采用决策控制实现可调容积附加气室空气悬架的半主动控制。结果表明,基于参数优化结果的决策控制能有效提高悬架的综合性能,降低车身加速度和悬架动行程,但轮胎动载荷略有增加。
空气悬架;附加气室;多目标优化;决策控制
前言
空气悬架由于其具有优良的隔振性能和高度可调的特点,在汽车领域被日益广泛应用。随着人们对车辆行驶平顺性和操纵稳定性要求的不断提高,悬架参数可调的半主动悬架成为空气悬架领域的重要发展方向。
可变容积附加气室应用于空气悬架系统可实现空气弹簧刚度可调,是一种典型的半主动空气悬架结构。为充分发挥空气悬架系统的优势,国内外学者提出了多种参数优化方法与半主动控制策略。文献[1]中设计了适用于空气悬架座椅的半主动模糊控制器。文献[2]中通过调节通流面积与附加气室容积实现空气悬架刚度与阻尼的控制。参数优化方面,正交试验法、遗传算法和神经网络等方法均有应用[3-5]。
针对当前研究中存在的参数优化与半主动控制策略相互孤立的问题,本文中将遗传优化算法与决策控制理论相契合,以车辆行驶平顺性、行驶安全性和操纵稳定性的综合性能最优为目标,提出可变容积附加气室的空气悬架多目标参数优化与决策控制方法,从而提升车辆在多工况下的综合动力学性能。
1 建立空气悬架1/4车辆动力学模型
1.1 带附加气室空气弹簧系统建模
图1为带附加气室空气弹簧的物理模型,主要包括空气弹簧、附加气室和连接二者的连接管路3部分。
模型中,空气弹簧是产生弹性支撑力的主体隔振部件;附加气室通常为用金属材料加工制作的刚性容器,与空气弹簧连接以增大空气弹簧的有效容积。
通常情况下,空气弹簧的变形速度不足10m/s,而空气弹簧内气体的压力波传播速度大于数百米每秒,即使空气弹簧内部气体存在某些不均匀性,也能够迅速得以消除,使气体的变化过程接近准平衡过程[6],故可假设空气弹簧内气体处于同一热力学状态。
取空气弹簧为控制体,则控制体内气体的压力、温度以及质量等状态参数均发生动态变化,且变化过程近乎绝热,故空气弹簧内气体近似为一变质量开口绝热系统,则根据热力学第一定律,有
(1)
式中:k为绝热指数;ps,Vs,ms分别为空气弹簧内气体的压力、体积及质量。
空气弹簧的系统热力学方程同样适用于附加气室,因此有
(2)
式中:pa,Va,ma分别为附加气室内气体的压力、体积及质量。
因附加气室为刚性容器,在振动状态下保持容积不变,因此式(2)简化为
(3)
连接管路会影响主、辅气室的气体流动,使系统产生延迟,故连接管路不能简单地等效为具有一定有效通流面积的小孔,而应等价为具有延迟效应的节流孔[6]。由文献[7]中可得到管路首末两端的流量关系为
式中:Rt为管路阻力系数;R为气体常数;P,T分别为管路末端气压与温度;t为时间;v为对应温度下的声速;L为管路长度。
连接管路首末两端流量可根据首末两端气压计算[6]:
(4)
式中:p1=max(ps,pa);p2=min(ps,pa);T1为p1端的气体温度;A为节流孔的有效流通面积。
1.2 1/4车辆动力学建模
可变容积附加气室空气悬架1/4车辆2自由度振动系统模型如图2所示。考虑到空气弹簧刚度特性的非线性,本文建模时将其以弹簧力的形式引入模型,以避免采用定刚度弹簧等效所带入的误差。
图2中,m1,m2分别为非簧载质量与簧载质量;F为空气弹簧非线性力;c为减振器阻尼;kt为轮胎刚度;z1,z2分别为非簧载质量和簧载质量的垂向位移;q为路面不平度输入。
(5)
式中:Ae为空气弹簧的有效面积,由空气弹簧试验数据拟合获得。
将可变容积附加气室空气弹簧热力学模型与1/4车辆动力学模型相结合,在Matlab/Simulink环境中搭建可变容积附加气室空气悬架1/4车辆Simulink仿真模型,如图3所示。
2 空气悬架系统多目标优化
2.1 多目标优化
评价悬架性能的指标一般为:代表乘坐舒适性的车身加速度;代表轮胎接地性能的轮胎动载荷;影响车身姿态且与结构设计和布置相关的悬架动行程[8]。
选取上述3个指标作为子目标函数,构建多目标优化模型,悬架动行程与轮胎动载荷还同时作为约束条件。多目标优化模型为
(6)
式中:Va为附加气室容积;fACC,fSWS及fDTL分别为车身加速度、悬架动行程及轮胎动载荷均方根值;ζ为悬架阻尼比;[fd]为悬架限位行程。
2.2 多目标优化处理
悬架参数的匹配关系决定悬架性能的优劣,各项性能在某种程度上相互制约,有时甚至相互矛盾[8],各子目标函数通常不能同时取得最优值。本文中采用线性加权和法赋予各子目标函数以权重,构造多目标优化的单目标评价函数。线性加权和法是在构建多目标优化问题的评价函数时,引入权重系数,代表各个子目标函数的相对重要程度。考虑到各子目标函数在量纲与量级上的差异,先对各子目标函数进行归一化处理,即将各子目标函数除以各自的最大值,再按照α-方法确定各子目标函数的加权系数[10],从而将多目标优化转化为单目标优化。
α-方法是综合考虑各项子目标函数的极小点信息后,赋予各项相应的加权系数。设车身加速度、悬架动行程和轮胎动载荷加权系数分别为w1,w2和w3,且
(7)
则引入参数α,可建立关于w1,w2,w3和α的4阶线性方程组:
(8)
式中:i=1,2,3。
利用式(7) 3个方程左侧参数构建系数矩阵:
(9)
则3个子目标函数的加权系数为
(10)
其中e=(1,1,1)T。
针对所研究的车辆结构参数及行驶工况,求得w1=0.5415,w2=0.3233,w3=0.1352,从而将式(6)中3个子目标函数整合为单目标函数:
(11)
2.3 参数优化结果
基于可变容积附加气室空气悬架1/4车辆Simulink仿真模型,结合上述讨论的可变容积附加气室空气悬架系统的多目标优化模型构建其处理方法,针对某款大型客车参数(表1),在Matlab环境下编写遗传算法优化程序[10],对悬架附加气室容积与减振器阻尼系数进行寻优。
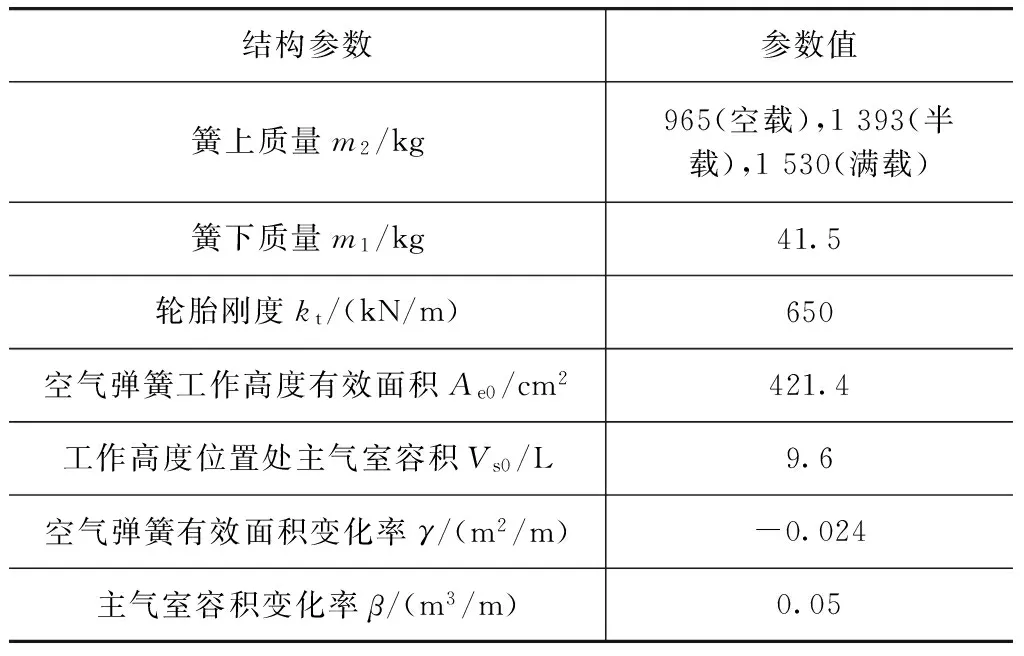
表1 1/4车辆模型结构参数表
结合行车实际,文中典型工况选择为:A级路面50~110km/h,B级路面40~80km/h,C级路面30~60km/h。载荷选取空载、半载及满载。整合后的优化结果如表2~表4所示。
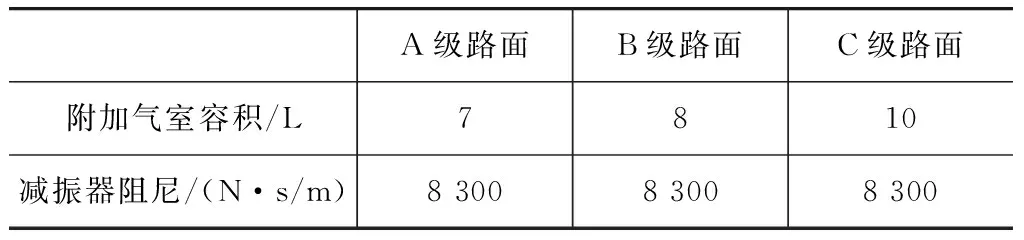
表2 满载时附加气室容积与减振器阻尼
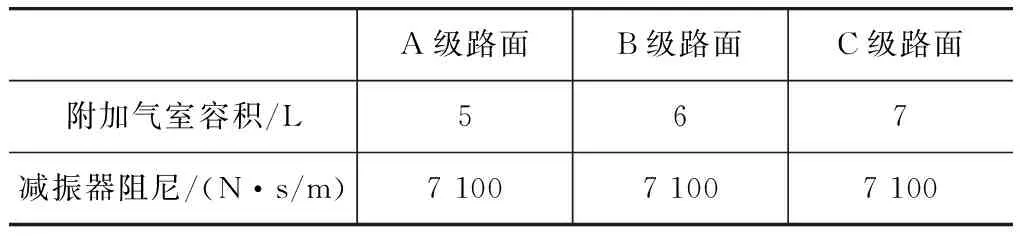
表3 半载时附加气室容积与减振器阻尼
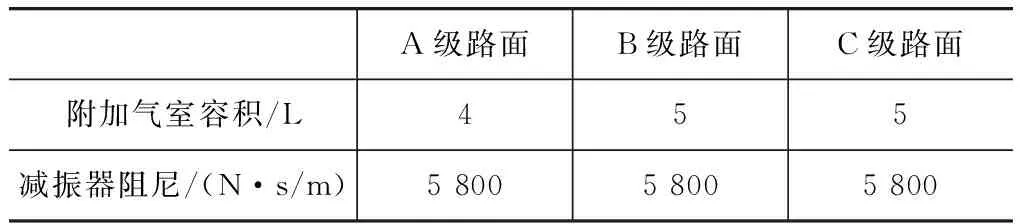
表4 空载时附加气室容积与减振器阻尼
3 可变容积附加气室空气悬架的决策控制
3.1 决策控制流程
决策控制在实际应用中具有良好的鲁棒性、容易实现及应用成本低等优点,故本文中选择决策控制作为可变容积附加气室空气悬架系统的半主动控制策略。
决策控制是指事先采用某种优化算法获取对应于车辆载荷、路面状况和行驶车速等车辆工况的悬架刚度与阻尼的优化值,并按照一定规则将优化结果编制成表格,存入车辆电子控制单元;实施决策控制时,根据车辆载荷、路面状况和行驶车速等工况信息,控制器判断被控对象处于何种状态,并按照判断结果查找控制单元内对应工况的悬架刚度与阻尼值,然后控制执行机构实施控制。图4为空气悬架的决策控制流程图。
3.2 行驶工况判断
由1/4车辆模型仿真可得,当车辆载荷处于空载与半载之间时,车辆在A级路面的悬架动行程均方根fSWS<4.4mm,B级路面4.6mm
由此可知,不同等级路面下,车辆的悬架动行程均方根有明显分界。利用悬架动行程均方根来识别路面等级,且为避免悬架动行程均方根在分界线附近波动导致的附加气室容积不断往复切换,在不同等级路面之间设置了滞回区间,如图5所示。例如,空载-半载载荷条件下A级与B级路面间的滞回区间为4.4~4.6mm,即当车辆悬架动行程均方根值超过4.6时,辨识当前路面状况达到B级,控制系统按B级路面查询控制规则表,并令执行机构调节附加气室容积从而改变悬架刚度;当路面状况转好,悬架动行程降低至4.4mm以下,按A级路面控制悬架刚度;4.4~4.6mm范围内不执行刚度调节。
车辆载荷可根据气压传感器测量的空气弹簧内气体压力(一段时间内的平均值)获得,车辆行驶车速可由车速传感器测量的速度信号获取。
3.3 决策控制结果
为验证本文采用的控制方案的有效性,选取A级路面80km/h—B级路面60km/h—C级路面50km/h的混合随机路面作为可变容积附加气室空气悬架系统的路面激励,并比较实施决策控制前后悬架性能的变化。图6为随行驶工况改变,在控制系统作用下附加气室容积的变化。由于载荷状态保持满载,该过程中未触发减振器阻尼调节。
表5为决策控制前后,A级路面80km/h—B级路面60km/h—C级路面50km/h混合路面下车辆动态性能对比情况。由表5可知,施加控制后,车身垂向加速度和悬架动行程得到有效抑制,轮胎动载荷有所增加,加权所得车辆综合性能提升约8.8%。

表5 控制前后悬架性能对比表
4 结论
(1) 应用工程热力学与流体力学理论,建立带附加气室的空气弹簧数学模型,并与车辆动力学模型结合,构建了可变容积附加气室空气悬架1/4车辆模型。
(2) 基于典型工况下的悬架多目标优化模型,采用遗传优化算法对空气弹簧的附加气室容积与减振器阻尼系数进行寻优,实现行驶平顺性、轮胎接地性和操纵稳定性的综合性能最优。
(3) 根据悬架系统的多目标优化结果,以决策控制为控制策略设计悬架的半主动控制方案。结果表明,决策控制有效提高了悬架的综合性能,降低了车身加速度、悬架动行程,但轮胎动载荷有所增加。
[1] Huseinbegovic S, Tanovic O. Adjusting Stiffness of Air Spring and Damping of Oil Damper Using Fuzzy Controller for Vehicle Seat Vibration Isolation[C]. Control and Communications, 2009. SIBCON 2009. International Siberian Conference on,IEEE,2009:83-92.
[2] Alonso A, Giménez J G, Nieto J, et al. Air Suspension Characterisation and Effectiveness of a Variable Area Orifice[J]. Vehicle System Dynamics,2010,48(S1):271-286.
[3] 陈静,曹晓琳,王登峰.重型商用车驾驶室空气悬置系统的匹配优化[J].吉林大学学报(工学版),2009,39(5):1125-1129.
[4] 程悦.客车空气悬架系统优化匹配技术及试验研究[D].长春:吉林大学,2012,6.
[5] Porumamilla H, Kelkar A G, Vogel J M. Modeling and Verification of an Innovative Active Pneumatic Vibration Isolation System[J]. Journal of Dynamic Systems, Measurement and Control,2008,130:1-12.
[6] 沈维道,童钧耕.工程热力学[M].北京:高等教育出版社,2007.
[7] Edmond R, Yildirim H. A High Performance Pneumatic Force Actuator System Part1-Nonlinear Mathematical Model[J]. ASME Journal of Dynamic Systems Measurement and Control,2000,122(3):416-425.
[8] 杨启耀.ECAS客车悬架系统的匹配与充放气研究[D].镇江:江苏大学,2008.
[9] 胡琉达.实用多目标最优化[M].上海:上海科技出版社,2006.
[10] 雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
Parameter Optimization and Control of Air Suspensionwith Adjustable Auxiliary Chamber
Li Zhongxing1, Ju Longyu1, Jiang Hong2& Huang Dingshi3
1.SchoolofAutomobileandTrafficEngineering,JiangsuUniversity,Zhenjiang212013; 2.SchoolofMechanicalEngineering,JiangsuUniversity,Zhenjiang212013; 3.BoschinBoschAutomotiveProducts(Suzhou)Co.,Ltd.,Suzhou215000
A mathematical model for the air suspension with adjustable auxiliary chamber is developed based on thermal dynamics and vehicle dynamic theories, and a multi-objective optimization model for air suspension with auxiliary chamber is constructed with enhancing the ride comfort, tire grip and handling stability of vehicle as objectives and the volume of auxiliary chamber and the damping coefficient of shock absorber as design variables. Then the multi-objective optimization model is converted to single-objective optimization model by using linear weighting method. Finally, the results of optimizations in typical conditions are integrated, and with loads, road grades and vehicle speeds as control input, decision-making control is adopted to achieve the semi-active control of air suspension with adjustable auxiliary chamber. The results show that the decision-making control based on optimized parameters can effectively enhance the overall performance of suspension, reduce vehicle body acceleration and suspension dynamic travel with slightly increased tire dynamic load.
air suspension; auxiliary chamber; multi-objective optimization; decision-making control
*国家自然科学基金(51075190)、国家青年科学基金(51305111)和江苏省“六大人才高峰”高层次人才计划(2012-ZBZZ-30)资助。
原稿收到日期为2013年7月3日,修改稿收到日期为2014年5月6日。
