两种典型轿车前悬架运动特性的对比研究*
2015-04-12兰凤崇陈吉清
熊 飞,兰凤崇,陈吉清,李 罡
(1.华南理工大学机械与汽车工程学院,广州 510640; 2.广州汽车工业集团汽车工程研究院,广州 511434)
2015198
两种典型轿车前悬架运动特性的对比研究*
熊 飞1,2,兰凤崇1,陈吉清1,李 罡1,2
(1.华南理工大学机械与汽车工程学院,广州 510640; 2.广州汽车工业集团汽车工程研究院,广州 511434)
为了从定性和定量的角度全面揭示麦弗逊式和双横摆臂式两种悬架的运动特性及其影响规律,以最小化车轮定位参数、侧倾中心高度和抗点头率等参数梯度的绝对值为目标,采用悬架运动学参数对硬点坐标的灵敏度分析和运用遗传算法进行运动学特性优化相结合的方法,对比分析了这两种悬架的运动学特性,通过试验验证了优化结果,最后给出了汽车开发过程中对这两种悬架选型的建议。
轿车;前悬架;运动学特性;灵敏度分析;遗传算法
前言
汽车悬架类型的选择和悬架运动学性能的设计对车辆的操纵稳定性、平顺性、制动安全性[1-4]等都有重要的影响。因此,汽车正向开发过程中,不同结构形式的悬架的运动学性能的差异是悬架类型的选择及匹配需要最优先考虑的问题。
目前,麦弗逊式悬架和双横臂式悬架是汽车前悬架中应用最广泛的两种类型的悬架。国内外学者对这两种悬架也做了很多研究[5-7],这些研究的结果表明,麦弗逊式悬架结构简单,簧载质量小,占用空间小,响应较快,制造成本低,而双横臂式悬架对前轮定位参数的变化设定自由度较大,有利于提高车轮稳定性等。但是,还需要对比研究这两种悬架运动学性能本质上的差异,以及在车辆开发过程中如何进行精细考虑悬架选型。
悬架的K特性是悬架运动学(Kinematics)的简称,描述的是车轮定位参数在悬架上下跳动和转向时的变化;悬架的C特性是悬架弹性运动学(Compliance)的简称,描述的是由于轮胎与地面之间的力和力矩作用引起的车轮定位参数的变化。二者统称为悬架运动学和弹性运动学特性,简称为悬架K&C(Kinematics & Compliance)特性。
本文中结合自主品牌轿车悬架开发选型工作,以车轮定位参数、侧倾中心高度、抗点头率等参数为研究对象,建立了两种悬架的分析仿真模型,采用将悬架硬点运动学灵敏度和运动学性能分析优化相结合的方法,对比分析了麦弗逊式前悬架和双横臂式悬架运动学性能的优缺点,通过试验优化计算的部分结果,对两种悬架的性能做了比较分析并给出了汽车开发过程中悬架选型建议。
1 悬架硬点灵敏度分析
1.1 两种悬架试验模型的建立
本文中在ADAMS/CAR软件中分别建立1/2车辆麦弗逊式悬架和双横臂式悬架模型。悬架系统坐标系以车辆前进行驶方向的反方向为x轴正方向,以同轴车轮由左指向右方向为y轴正方向,以垂直地面向上方向为z轴正方向。根据已知的麦弗逊式悬架硬点、部件参数和拓扑结构关系建立其多体模型。同时对麦弗逊式悬架进行简化,演变出双横臂式悬架。为了使两种悬架具有可比性,要做到两种悬架车轮定位参数、弹簧刚度、减振器阻尼特性、簧上质量等完全相同。
1.2 两种悬架车轮定位参数
两种悬架拓扑结构试验模型如图1和图2所示。Pt0/Pt0′代表作为计算车轮定位参数用的车轮中心外参考点,它由车轮中心沿y轴方向向外移动100mm而得,Pt1/Pt1′代表下摆臂与副车驾的前连接点,Pt2/Pt2′代表下摆臂与副车驾的后连接点,Pt3/Pt3′代表下摆臂与转向节的连接点,Pt4/Pt4′代表转向拉杆与转向节的连接点,Pt5/Pt5′代表转向拉杆与转向器的连接点,Pt6′代表上摆臂与车身支座的前连接点,Pt7′代表上摆臂与车身支座的后连接点,Pt8/Pt8′代表麦弗逊式悬架减振器的上安装点和双横臂式悬架上摆臂与转向节的连接点,Pt9/Pt9′代表车轮中心点。当已知两种悬架以上硬点时,可以通过悬架三维硬点坐标求出车轮定位参数[1]如下:
(1)
(2)
γ=yPt9/Pt9′-yPt0/Pt0′
(3)
ξ=xPt9/Pt9′-xPt0/Pt0′
(4)
(5)
式中:α为车轮前束角;β为车轮外倾角;γ为轮距变化;ξ为轴距变化;ψ为主销后倾。
1.3 悬架运动学灵敏度分析
本文中应用参数试验法进行悬架运动学灵敏度分析,即求取悬架诸运动学参数对各硬点坐标变化的敏感性。本文中研究以两种悬架各硬点坐标偏离设计值±0.5mm为因子水平,计算两水平因子间悬架的前束角梯度等5种梯度和侧倾中心高度与抗点头率共7个响应。
车轮定位参数梯度表示车轮轮心基于设计位置上下跳动±25mm时,车轮定位参数的变化量与轮心行程的比值。
表1和表2分别示出两种悬架的运动学参数灵敏度分析的结果。由表1和表2可以看出,麦弗逊式悬架车轮外倾角梯度和主销后倾角梯度对硬点坐标变化的灵敏度较低,悬架设计时外倾角梯度和主销后倾角梯度较难优化,车轮定位参数匹配的灵活性较低。而双横臂式悬架诸运动学参数对各硬点坐标变化的灵敏度都较高,更容易进行车轮定位参数匹配。
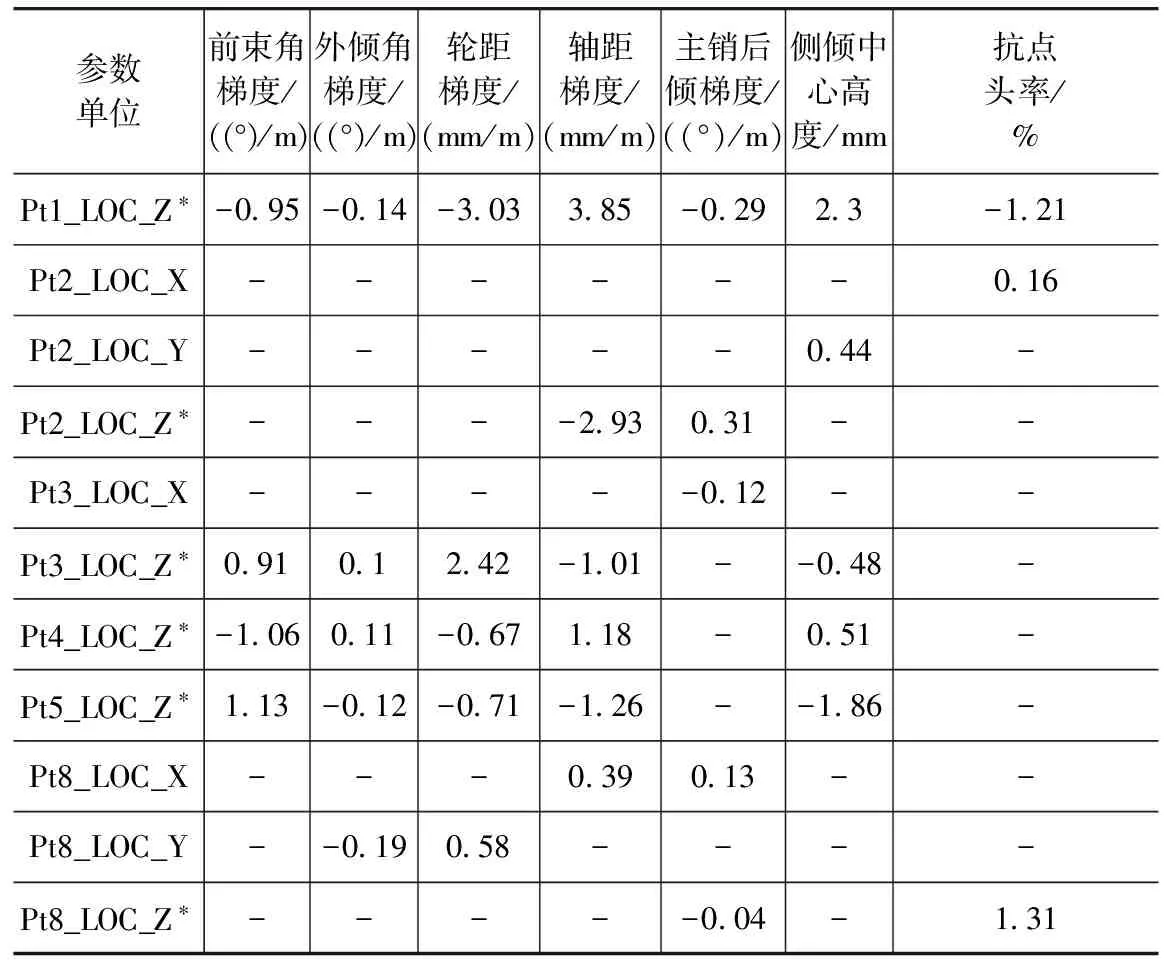
表1 麦弗逊式悬架运动学灵敏度分析结果

表2 双横臂式悬架运动灵敏度分析结果
麦弗逊式悬架总共有6个硬点的6个方向(表1中带*号者)对悬架运动学特性影响较大,而双横臂式悬架总共有8个硬点的8个方向(表2中带*号者)对悬架运动学特性影响较大,双横臂式悬架运动学特性设计的自由度较大。
2 两种悬架运动学性能的优化
遗传算法是一种基于自然选择和群体进化机制,适合数值求解多参数、多变量、多目标的优化问题,在寻求全局最优解方面具有高效率的参数优化方法。遗传优化面对群体采用概率转移规则,可同时对多个优化参数进行全域寻优。因此,本文中采用遗传算法对悬架运动学性能参数进行优化[8]。
为了保证车辆有良好的操纵稳定性和较小的轮胎磨损量,本文中以车轮前束角变化梯度、车轮外倾角变化梯度、车轮轮距变化梯度、车轮轴距变化梯度和主销后倾角变化梯度绝对值的最小化作为优化目标。
minF=[fToe,fCamber,fTrack,fBase,fCaster]T
(6)
式中:fToe为车轮前束角变化;fCamber为车轮外倾角变化;fTrack为车轮轮距变化;fBase为车轮轴距变化;fCaster为主销后倾角变化;α,β和ψ的下标“+”和“-”分别表示车轮向上和向下移动25mm时的参数值。悬架构建硬点的空间位置决定了悬架的车轮定位参数运动规律,因此选取悬架各个硬点的三坐标值(xi,yi,zi)为设计变量。为了满足整车抗侧倾和抗俯仰性能要求,选择悬架侧倾中心高度和抗点头率为约束条件。
(7)
式中:σi和τi分别为侧倾中心高度和抗点头率。为了满足整车总布置避免干涉发生等要求,各设计变量也必须在一定范围内:
(8)
悬架运动学特性对整车操作稳定性有重要影响,因此本文中基于两种悬架试验模型,分别进行同向轮跳试验,轮跳范围为-80~+80mm,分别从车轮定位参数、轴距、轮距、侧倾中心、抗点头率等7个方面进行分析对比。
2.1 同向轮跳前束角变化
前轮前束角与车轮跳动关系仿真结果曲线如图3所示。从图中曲线可以求出,车轮在-25~+25mm内跳动时,麦弗逊式悬架轮跳前束角梯度为-4.6°/m,经过优化后轮跳前束角梯度为-4.1°/m,双横臂式悬架轮跳前束角梯度为-2.7°/m,经过优化后轮跳前束角梯度为-5.3°/m。两种悬架前束角梯度都在较理想范围(-6~-2°/m)[9]内。当车轮向上跳动到极限时,麦弗逊式悬架的前束角增大较快,双横臂式悬架的前束角变化线性度较好。
2.2 同向轮跳外倾角变化
同向轮跳外倾角与车轮跳动关系仿真结果曲线如图4所示。从图中曲线可以求出,车轮在小范围(-25~25mm)内跳动,轮跳外倾角梯度为-7.3°/m,经过优化后轮跳外倾角梯度为-7.9°/m。双横臂式悬架轮跳外倾角梯度为-15.1°/m,经过优化后轮跳外倾角梯度为-13.5°/m。当车轮向上跳动到极限时,麦弗逊式悬架的外倾角缓慢增大,双横臂式悬架的外倾角急剧下降;当车轮向下剧烈跳动时,则情况相反,麦弗逊式悬架的外倾角出现急剧增大的情况,双横臂式悬架的外倾角缓慢增大,双横臂式的轮跳外倾曲线更有利于增加轮胎的抓地力,有利于车辆极限侧向加速度下的行驶稳定性。
2.3 同向轮跳轴距变化
同向轮跳轴距与车轮跳动关系仿真结果曲线如图5所示。从图中曲线可以求出,车轮在小范围(-25~25mm)内跳动,麦弗逊式悬架轮跳轴距变化梯度为-19.4mm/m,经过优化后轴距变化梯度为-16.8mm/m。双横臂式悬架轮跳轴距变化梯度为-30.3mm/m,经过优化后轴距变化梯度为-29.2mm/m。当车轮向上剧烈跳动时,麦弗逊式悬架的轴距变化梯度缓慢增大,双横臂式悬架的轴距变化梯度变化较快。在设计状态,麦弗逊式悬架比双横臂式悬架纵向舒适性要好。
2.4 同向轮跳轮距变化
同向轮跳轮距与车轮跳动关系仿真结果曲线如图6所示。从图中曲线可以求出,车轮在小范围(-25~25mm)内跳动,麦弗逊式悬架车轮轮距变化梯度为-33.4mm/m,经过优化后轮距变化梯度为-39mm/m。双横臂式悬架车轮轮距梯度为-57.8mm/m,经过优化后轮距梯度为35mm/m。优化后,当车轮向上剧烈跳动时,麦弗逊式悬架的轮距变化梯度变化较快。在设计状态,麦弗逊式悬架比双横臂式悬架纵向轮胎偏磨风险要高。
2.5 同向轮跳主销后倾角
主销后倾角与车轮跳动关系仿真结果曲线如图7所示。从图中曲线可以求出,车轮在小范围(-25~25mm)内跳动,麦弗逊式悬架主销后倾角变化梯度为13.8°/m,优化后主销后倾角变化梯度为13.5°/m。双横臂式悬架主销后倾角变化梯度为5.7°/m,经过优化后主销后倾角梯度为10.1°/m。但是当车轮向上或向下剧烈跳动时,双横臂式悬架主销后倾角都比设计状态要大,同时变化比较快,这样有利于增加制动俯仰时车轮回正性等。
2.6 悬架抗点头率
悬架抗点头率与车轮跳动关系仿真结果曲线如图8所示。从图中可以看出,在车轮跳动为零时,麦弗逊式悬架抗点头率为26%,经过优化后悬架抗点头率为31%。双横臂式悬架抗点头率为20%,经过优化后悬架抗点头率为28%。虽然在轮跳为零时,麦弗逊式悬架抗点头率比双横臂式悬架大,但是随着轮跳增加,双横臂式悬架抗点头率增加较快,所以双横臂式悬架也可以获得较好的抗点头性能。
2.7 同向轮跳侧倾中心
侧倾中心位置与车轮跳动关系仿真结果曲线如图9所示。从图中可以看出,在轮跳为零时,麦弗逊式悬架侧倾中心高度为23mm,经过优化,侧倾纵向高度为31mm。双横臂式悬架侧倾中心高度为48mm,经过优化,侧倾中心高度为35mm。麦弗逊式悬架的侧倾中心低于双横臂式悬架,并且随着车轮向上跳动增加,麦弗逊式悬架侧倾中心下降比双横臂式要快,因此双横臂式悬架具有更高的侧倾稳定性。
3 试验与优化结果对比
以上麦弗逊式悬架运动学性能优化结果最终被应用到某自主品牌轿车前悬架设计过程中,为了验证优化结果,进行K&C台架试验(见图10)。汽车悬架K&C特性试验台是专门用来测量悬架运动学特性和弹性运动学特性的试验设备,采用准静态加载方式,将车身固定,然后通过给车辆施加4个方向的载荷,测试车轮定位等参数变化,对比试验与优化设计结果差异。
试验要求:
(1) 车轮垂直力加载范围:0~10 000N;垂直行程:±150mm;
(2) 车身固定,限制车身的任何运动;
(3) 车轮制动,限制车轮的转动。
试验步骤:
(1) 首先明确试验车辆信息和试验要求,按照试验车辆的轴距、轮距调整试验台加载墩的位置和加载方向到初始零位置;
(2) 调整车辆配重,使用吊具将试验车辆吊装到试验台上,测量各个车轮的载荷,将4个加载墩加载到试验车设计轮荷值,使用夹具固定车身的裙边。利用制动踏板锁止器将被测车辆的制动踏板固定,以限制车轮的转动;
(3) 安装车轮测量系统及其倾角传感器和转向系统转矩、转角信号线等;
(4) 按照要求,完成各工况试验。
图11是样车麦弗逊式悬架前束角随轮跳变化优化和试验结果的对比,车轮在范围(-25~+25mm)内跳动,前束角梯度测量结果为-4.3°/m,与优化分析结果绝对值差值只有0.2°/m,并且从试验测量曲线看出,样车悬架前束角变化曲线性度较好,能满足性能设定要求。
图12是样车麦弗逊式悬架外倾角随轮跳变化优化和试验结果的对比,车轮在范围(-25~+25mm)内跳动,外倾角测量结果为-8.5°/m,与优化分析结果绝对值差异只有0.6°/m,并且从试验测量曲线看出,试验与优化曲线吻合度较好,样车车轮外倾角能满足性能设定要求。
图13是样车麦弗逊式悬架轴距随轮跳变化优化和试验结果的对比,车轮在范围(-25~+25mm)内跳动,轴距变化梯度测量结果为-18.7mm/m,与优化分析结果绝对值差异只有2.1mm/m,并且从试验测量曲线看出,试验与优化曲线吻合度较好,样车轮跳轴距变化能满足性能设定要求。
图14是样车麦弗逊式悬架轮距随轮跳变化优化和试验结果的对比,车轮在范围(-25~+25mm)内跳动,轴距变化梯度测量结果为-45mm/m,与优化分析结果绝对值差异有6mm/m,并且从试验测量曲线看出,试验与优化曲线趋势吻合度较好,样车轮跳轮距变化基本满足性能设定要求。
4 结论
通过优化这两种悬架,都能得到:较好的轮跳转向性能、车轮回正性和抗点头性能,有利于车辆的行驶稳定性。在设计状态时麦弗逊式悬架的抗点头性能比双横臂式悬架好,但是随着车轮上跳量增加,双横臂式悬架抗点头性逐渐提高。从轴距变化梯度来看,麦弗逊式悬架纵向舒适性比双横臂式悬架好。
麦弗逊式悬架运动学参数(特别是车轮外倾角和主销后倾角)对硬点坐标变化的灵敏度比双横臂式悬架低,故其设计自由度小。从优化结果可以看出,麦弗逊式悬架外倾角梯度优化前后的变化较小,这决定了在较大侧向加速度时车辆的稳定性较弱。双横臂式悬架可以获得较高的侧倾中心高度,同时车轮轮距变化梯度相对较小,说明它既可获得较好的抗侧倾性能,又能获得较小的轮胎偏磨。
两种悬架在运动学性能方面的区别决定了悬架有不同的应用领域。建议对于前轴轴荷较大的车辆优先考虑采用双横臂式悬架,这样前轴稳定杆可以设定较细,以便在不牺牲舒适性的同时,保证车辆有较好的行驶稳定性和抗侧倾性能。反之,可以优先考虑采用麦弗逊式悬架,它能在满足一定的操稳性能要求的同时降低成本。
[1] 陆建辉,周孔亢.电动汽车麦弗逊前悬架设计及参数优化[J].机械工程学报,2012(8):98-103.
[2] 上官文斌,王江涛.全地形越野车前双横臂独立悬架与转向系统的设计分析[J].汽车工程,2008,30(4):345-348.
[3] Hosein Habibi, Kourosh H Shirazi, Mohammad Shishesaz. Roll Steer Minimization of McPherson-strut Suspension System Using Genetic Algorithm Method[J]. Mechanism and Machine Theory,2008(43):57-67.
[4] Seong Jun Park, Jenong Hyun Sohn. Effects of Camber Angle Control of Front Suspension on Vehicle Dynamic Behaviors[J]. Journal of Mechanical Science and Technology,2012(2):307-313.
[5] 汤林生,易高.双球头型双横臂前悬架系统的开发[J].汽车工程,2011,33(1):56-59.
[6] Hazem Ali Attia. Dynamic Modelling of the Double Wishbone Motor-Vehicle Suspension System[J]. European Journal of Mechanics,2002(21):167-174.
[7] Mahmoodi-Kalerbar M, Javanshir I, Asadi K, et al. Optimization of Suspension System of Off-road Vehicle for Vehicle Performance improvement[J]. Journal of Central South University,2013,20(4):902-910.
[8] Baumal A E, McPhee J J, Calamai P H. Application of Genetic Algorithms to the Design Optimization of an Active Vehicle Suspension System[J]. Computer Methods in Applied Mechanics and Engineering,1998(163):87-94.
[9] 耶尔森·赖姆帕尔.汽车底盘基础[M].张洪欣,余卓平,译.北京:科学普及出版社,1992:136-176.
A Comparative Study on the Kinematic Characteristicsof Two Typical Front Suspensions of Sedan
Xiong Fei1,2, Lan Fengchong1, Chen Jiqing1& Li Gang1,2
1.SchoolofMechanical&AutomotiveEngineering,SouthChinaUniversityofTechnology,Guangzhou510640; 2.AutomotiveEngineeringInstitute,GuangzhouAutomobileGroupCo.,Ltd.,Guangzhou511434
For qualitatively and quantitatively revealing the kinetic characteristics of McPherson suspension and double wishbone suspension and their law of influence, with minimizing the absolute values of gradients of wheel alignment parameters, roll center height and anti-dive rate as objective, the kinetic characteristics of two types of suspension are comparatively analyzed by using sensitivity analysis of suspension kinetic parameters to the coordinates of hard-points, combined with kinetic characteristics optimization with genetic algorithm. The results of optimization are verified by tests. Finally a recommendation on the selection of two types of suspension in the process of vehicle development is given.
sedan; front suspension; kinematic characteristics; sensitivity analysis; genetic algorithm
*广东省战略性新兴产业专项资金项目资助。
原稿收到日期为2013年12月3日,修改稿收到日期为2014年4月24日。
