尾缘襟翼长度对风力机翼型气动性能的影响
2015-04-11韩中合贾亚雷李恒凡朱霄珣
韩中合,贾亚雷,2,*,李恒凡,朱霄珣,董 帅
(1.华北电力大学电站设备状态监测与控制教育部重点实验室,河北保定 071003;2.河北软件职业技术学院,河北保定 071000)
尾缘襟翼长度对风力机翼型气动性能的影响
韩中合1,贾亚雷1,2,*,李恒凡1,朱霄珣1,董 帅1
(1.华北电力大学电站设备状态监测与控制教育部重点实验室,河北保定 071003;2.河北软件职业技术学院,河北保定 071000)
针对尾缘襟翼长度对风力机翼型气动性能的影响,分别以S809翼型与DU翼型为研究对象,设计了6种襟翼长度的襟翼模型,襟翼向翼型压力面偏转角为10°,襟翼与翼型主体之间为均匀1mm间隙,利用AUTOCAD对各襟翼长度模型进行几何建模。采用计算流体力学软件Fluent 14.0对各襟翼模型进行不同攻角下的气动性能计算,对翼型边界附近流场及压力系数等进行了分析比较。结果表明:尾缘襟翼长度对翼型的气动性能有较大的影响,襟翼长度不仅对襟翼附近的流场产生影响,对整个翼型的流场都有较大影响;带襟翼模型升力系数比无襟翼模型大大提高,且在一定攻角范围内随着襟翼长度增加,升力系数逐渐增大;带襟翼模型阻力系数比无襟翼模型翼型大,且在一定攻角范围内随襟翼长度增大阻力系数也增大;带襟翼模型升阻比在一定范围内比无襟翼模型大。
风力机翼型;分离式尾缘襟翼;计算流体力学;升阻比
0 引 言
近年来,风力发电得到迅速发展。叶片是风力发电机组捕捉风能的关键部件,其翼型升阻力特性对风力机的整体气动性能有较大的影响。风力机叶片后缘增加襟翼可以在一定范围内提高风力机翼型的升力及升阻比,提高风力机低风速时的捕风能力,进而提高风力机的发电量[1]。利用风力机襟翼装置还可以有效控制风力机叶片上的局部载荷,降低风力机叶片的疲劳载荷和风力机传动系统以及塔架上的载荷,提高了叶片及其他关键零部件的寿命,从而降低风力机的度电成本[2-4]。
国内外研究人员在提高风力机翼型升力方面进行了广泛研究。在各种提高翼型升力的方法及装置中,翼型尾缘添加襟翼可以显著提高翼型的升力以及升阻比。目前所研究的襟翼主要有Gurney襟翼、微型滑动襟翼(MICROTAB)、分离式尾缘襟翼以及可变形尾缘襟翼。国内外学者对加装Gurney襟翼的翼型气动性能进行了大量的研究,研究结果表明:翼型尾缘加装Gurney襟翼在一定范围内能够改善翼型附近流场分布及翼型的压力系数分布,进而可提高翼型升力及升阻比,改善翼型的综合气动性能[5-8]。李仁年等采用Fluent对加装Gurney襟翼和改进的钝尾缘翼型气动特性进行了计算分析,提出加装Gurney襟翼和钝尾缘改进翼型气动性能均优于原型[9]。张旭等研究了襟翼高度和压力面光滑连接襟翼顶端的开始位置对翼型气动性能的影响[10]。Troldborg利用CFD方法对固定尾缘襟翼进行了定常计算,表明固定尾缘襟翼能提高翼型升力,还可以在一定程度上减小载荷波动[11]。李传峰研究了可变形尾缘襟翼气动性能,提出可变形尾缘襟翼可以提高翼型的综合气动性能[12]。C P Van Dam等人验证了MICROTAB可以改善翼型附近的流场及压力系数分布,在一定范围内提高翼型的升力及升阻比[13]。王荣等深入研究了利用桨叶后缘小翼对直升机桨毂振动载荷及旋翼动态失速的控制[14]。Lackner和Kuik[15]等研究了分离式尾缘襟翼对5MW上风向风力机疲劳载荷的影响,验证了在叶片展向0.7R~0.9R位置添加襟翼,可以使叶片挥舞力矩降低12%~15%。
以上各种方法都可以增大翼型升力和升阻比,并在一定程度上可以降低叶片的载荷波动及极限载荷,但是也存在各自的缺点。Gurney襟翼与原翼型连接强度上会带来新问题[9];MICROTAB虽然控制简单方便,但其制造成本很高[13];可变形尾缘襟翼在提高升力和升阻比方面效果较好,但其结构复杂,且不易实现角度控制。相比之下分离式尾缘襟翼不但能提高升力和升阻比[16],又避免了连接部位出现强度不足问题,并且其制造成本也相对较低,容易实现变角度控制。国内外对于分离式尾缘襟翼的研究仅限于固定偏转角及固定襟翼长度下对翼型的气动性能进行分析,没有文献研究襟翼长度对翼型的气动性能的影响,对于如何确定最优的襟翼长度也没有进行深入研究。
本文以风力机翼型S809为研究对象,设计了5%、10%、15%、20%、25%、30%六种襟翼长度的分离式尾缘襟翼模型,并利用计算流体力学商用软件Fluent 14.0对各襟翼模型进行了计算,分析比较了各种模型的气动特性,找出了襟翼长度对翼型气动性能影响规律。
1 尾缘襟翼模型
1.1 几何模型
由于风力机翼型S809试验研究充分,试验数据丰富可靠,为了方便与试验数据对比,取S809翼型作为研究对象,翼型弦长设为1000mm。在S809翼型距尾缘a倍的弦长位置增加尾缘襟翼并建立尾缘襟翼几何模型如图1,其中a分别为5%、10%、15%、20%、25%、30%,各种模型尾缘襟翼与翼型本体之间保留1mm间隙,尾缘襟翼向翼型压力面偏转10°。

图1 S809分离式尾缘襟翼几何模型Fig.1 Model of airfoil S809with discrete trailing edge flap
1.2网格划分及边界条件
在相同算法下,采用均匀分布的正交网格计算能获得较高的计算精度[17],本文应用GAMBIT网格划分软件,利用多块网格生成技术生成了正交性好的结构化网格。为了避免入口边界和出口边界干扰,计算域入口距翼型前缘20倍弦长,计算域出口距翼型后缘20倍弦长,翼型距上下边界分别为20倍弦长。定义计算域左侧半圆边界为速度入口边界条件,定义右侧边界为压力出口边界条件,定义翼型上下面为无滑移壁面条件。为了提高边界层区域流场的模拟精度,要求近壁面第一层网格满足y+值约等于1。y+值过大会影响模拟精度。由于翼型前后缘及襟翼缝隙处的流动情况会对翼型数值模拟产生较大的影响,所以在翼型前缘、后缘及缝隙处进行了局部加密处理。为了分析网格的划分数量的影响,以保证计算结果的网格无关性,划分了105 000,154 800和200 000三种网格数模型,并进行计算。计算结果表明:前两种网格模型升力系数最大相差17%,而后两者最大相差为0.7%,由于154 800网格数模型网格数少,收敛快,所以选择154 800网格数模型为今后的比较模型,计算域网格结构见图2。
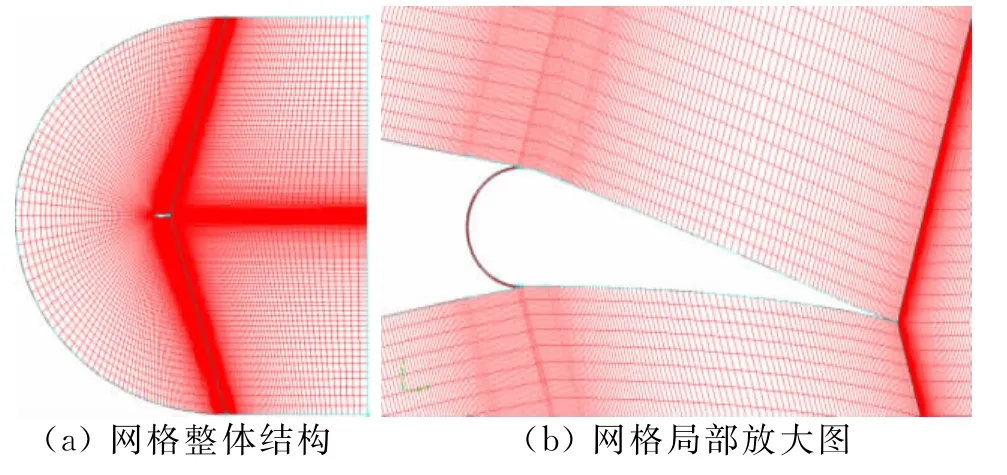
图2 模型网格图Fig.2 Grid structure of model
1.3 计算模型及相关参数
尾缘襟翼模型流场计算选用了商业软件Fluent 14.0,求解器选用了基于压力的定常求解器,压力-速度耦合选用SIMPLE算法,湍流模型选取k-ω二方程湍流模型,方程离散格式采用二阶迎风格式。为了与试验数值比较,计算条件为雷诺数Re=2×106,收敛标准为计算残差小于1×10-6,在上述条件下对无襟翼S809基准翼型进行了数值计算,来流攻角分别为0、1.02°、5.13°、9.22°、14.24°、20.15°。对于带襟翼模型的气动性能计算,固定襟翼偏转角为10°情况下,分别计算分析6种不同襟翼长度对翼型性能的影响。
2 计算方法可靠性验证
为验证所用算法的可靠性与合理性,对154 800网格数下风力机翼型S809在各攻角下的计算结果和试验数据[18-19]进行对比,翼型的计算数据及试验数据详见表1及图3。
表1为S809翼型的升阻力特性对比表。表1数据对比表明所选计算模型计算结果与参考文献的试验数据很接近。其中升力系数的计算值与试验值吻合很好,攻角为0°时相差为0.9%,攻角为1.02°时相差仅为0.2%。阻力系数计算值与试验值偏差较大,攻角为0°时相差为-4.3%,攻角为1.02°时相差-4.86%。当攻角接近失速攻角时,升阻力系数计算误差都较大,但升力系数最大误差小于8.06%,阻力系数最大误差小于10%。由于本文研究重点是襟翼长度对翼型气动特性的影响,属比较性研究,因此从表1中升阻力系数特性上看,计算所采用的模型计算法是可靠的。

表1 S809翼型升阻力系数比较Table 1 Comparison of lift and drag coefficient of S809airfoil
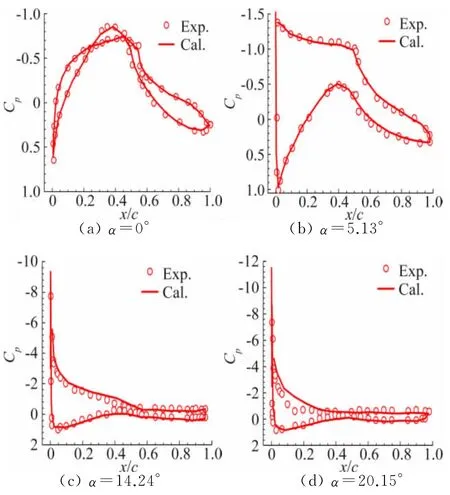
图3 无襟翼S809压力系数曲线Fig.3 Cpdistributions of airfoil without trailing edge flap
图3为不同攻角下压力系数分布曲线。由图3可看出S809翼型的压力系数计算结果和试验数据变化趋势相同,压力系数值可能稍有不同,但整体上和试验数据一致,从升阻力系数和压力系数角度分析,文章采取的计算方法合理可靠,完全可以满足后续襟翼模型的计算要求。
3 S809襟翼模型计算结果与分析
3.1 流线图分析
计算了6种长度襟翼的模型在不同攻角下的气动性能,对其每种工况的流场流线进行了分析比较,结果如图4。图中从左至右分别为5%、10%、15%、 20%、25%、30%弦长的尾缘襟翼模型的流线图。0°攻角时,5%弦长襟翼模型尾缘处出现分离现象不明显,随着襟翼长度增加,分离现象逐渐加大,襟翼长度为30%弦长时,尾缘处出现了明显的分离。随着攻角的增加,在模型尾缘处逐渐出现涡,并随攻角的增大而增大,随襟翼的长度增加,涡流强度也增加。8°攻角时,各襟翼模型都发生了明显的流动分离,并产生了分离涡,且随着襟翼长度的增加,分离涡逐渐加大,襟翼长度为30%弦长时,分离区已经扩展到襟翼连接处。攻角为16°,各模型已经处于失速,翼型吸力面呈现出更大的流动分离状态,并在尾缘处卷起反向涡。

图4 不同襟翼长度的模型流线图Fig.4 Streamlines of airfoil with different length trailing edge flaps
3.2 压力系数分布分析
为了找出不同襟翼长度对翼型表面压力系数的影响规律,在模型襟翼偏转角为10°时,比较了6种长度襟翼的模型在不同来流攻角下压力系数分布,见图5。襟翼长度与翼型弦长百分比分别为:5%、10%、15%、20%、25%、30%,来流攻角为0°、4°、8°、12°、16°。
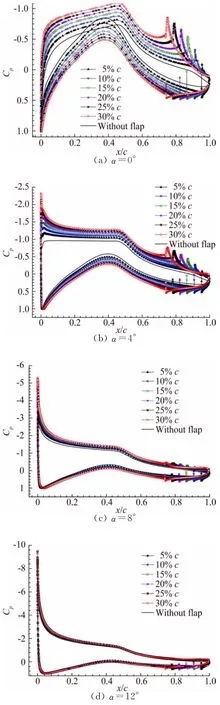

图5 不同襟翼长度的压力系数分布图Fig.5 Cpdistributions of airfoil with different length trailing edge flaps
图5表明,尾缘襟翼不仅影响尾缘襟翼附近压力系数,还会对整个翼型表面的压力系数分布产生影响。小攻角下,随着襟翼长度的增加,翼型的上下翼面压力差增加,长襟翼模型的压力系数曲线几乎将短襟翼模型的压力系数全部包围,仅剩下尾缘处;短襟翼模型上下压差仅在尾缘襟翼部分稍大于长襟翼模型压力差。随着攻角的增大,各种襟翼模型的压力系数之间差值逐渐减小,当攻角大于12°时,相差很小。
3.3 升阻力特性分析
3.3.1 升力系数比较
为了比较襟翼长度对翼型升力特性的影响,将襟翼向翼型压力面偏转固定为10°,计算分析了不同的襟翼长度的模型在不同攻角下的升力特性,结果如图6。图6中上面6条曲线分别为6种不同长度襟翼的模型升力系数随攻角变化的曲线,最下面一条为无襟翼的翼型升力系数曲线。图6表明带襟翼的模型升力系数均大于无襟翼模型升力系数,而且带襟翼的翼型升力系数曲线左移,失速攻角变小。小攻角时,升力系数随襟翼长度增加而增加,这是由于襟翼增大了翼型的弯度,且随襟翼长度增加,翼型的弯度也增大。当攻角为大于12°时,升力系数随着襟翼长度的先增加,当襟翼长度为25%弦长时,升力系数达到最大,之后随着襟翼长度的增加,升力系数减小。并且小攻角时,随着襟翼长度的增加,模型升力系数增加较快,然后随攻角的增加,模型升力系数随襟翼长度增加而提高的速度减小。
3.3.2 阻力系数比较
图7为在襟翼向翼型压力面偏转10°情况下,不同的襟翼长度在不同攻角下的阻力特性曲线。图7表明,带襟翼的翼型阻力系数均大于无襟翼模型的阻力系数,且随着攻角的增大,阻力系数增大。对于相同攻角的襟翼模型,随着襟翼长度的增加,翼型的阻力系数也增加。大于失速攻角后,翼型阻力迅速增加。

图6 不同襟翼长度的模型升力系数曲线Fig.6 Lift coefficients of airfoil with different length trailing edge flaps
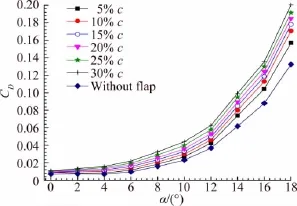
图7 不同襟翼长度的模型阻力系数曲线Fig.7 Drag coefficients of airfoil with different length trailing edge flaps
3.3.3 升阻比比较
图8为在襟翼向翼型压力面偏转10°情况下各种襟翼长度模型的升阻比比较。图8表明增加尾缘襟翼使得翼型的升阻比在小攻角时明显增加。在攻角为0°时,随襟翼长度增加,翼型的升阻比增加较明显;随着攻角的加大,升阻比随着襟翼长度增加而增加缓慢;攻角大于4°时,随着襟翼长度的增加翼型的升阻比反而下降。10%弦长襟翼在较宽的攻角范围内具有较大的升阻比。

图8 不同襟翼长度的模型升阻比曲线Fig.8 Lift drag ratio of airfoil with different length trailing edge flaps
4 DU30襟翼模型计算结果与分析
4.1 模型的选取
为了验证尾缘襟翼提高升力的通用性,还选取了风力机中常用的DU30翼型,分别建立了6种襟翼长度的襟翼模型,并采用Fluent 14.0对其进行气动性能分析。网格划分、计算模型选择及边界条件设定与前S809翼型算例的设定相同。
4.2 计算结果分析
4.2.1 升系数比较
图9为向翼型压力面偏转10°的不同襟翼长度DU翼型的升力系数比较。图9中上面6条曲线分别为6种不同长度襟翼的模型升力系数随攻角变化的曲线,最下面一条为无襟翼的翼型升力系数曲线。图9表明由于襟翼增大了翼型的弯度,使得带襟翼的模型升力系数均大于无襟翼模型升力系数。攻角小于6°时,各襟翼模型升力系数随襟翼长度增加而增加;攻角大于6°时,各襟翼模型升力系数随着襟翼长度的增加先增加,后减小。翼型的最大升力系数也随着襟翼长度的增加先增加,后减小。当襟翼长度为20%时,最大升力系数达到最大。并且模型在小攻角时,随着襟翼长度的增加,模型升力系数增加较快,然后随攻角的增加,模型升力系数随襟翼长度增加而提高的幅值减小。5%弦长模型与10%弦长模型提高升力系数效果明显,其他几种长度模型提高升力幅值较小。
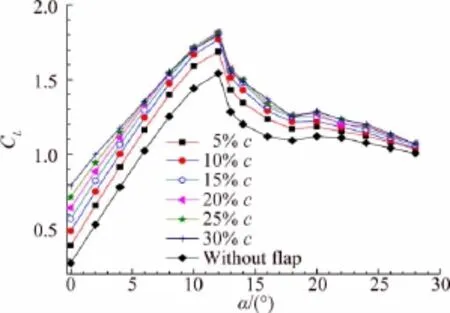
图9 不同襟翼长度的模型升力系数曲线Fig.9 Lift coefficients of airfoil with different length trailiy edge flags
4.2.2 阻力系数比较
图10为向翼型压力面偏转10°的不同的襟翼长度DU翼型在不同攻角下的阻力特性曲线。图10表明,带襟翼的翼型阻力系数均大于无襟翼模型的阻力系数,且随着攻角的增大,阻力系数增大。对于相同攻角的襟翼模型,随着襟翼长度的增加,翼型的阻力系数也增加。大于失速攻角后,翼型阻力迅速增加。

图10 不同襟翼长度的模型阻力系数曲线Fig.10 Drag coefficients of airfoil with different length trailing edge flaps
4.2.3 升阻比比较
图11为向翼型压力面偏转10°的不同的襟翼长度DU翼型模型的升阻比比较。图11表明增加尾缘襟翼使得翼型的升阻比在小攻角时明显增加。在攻角为0°时,随襟翼长度增加,翼型的升阻比增加较明显;随着攻角的加大,升阻比随着襟翼长度增加而增加缓慢;到攻角大于2°时,随着襟翼长度的增加部分襟翼模型升阻比反而下降。5%弦长襟翼模型具有最大的升阻比。10%弦长襟翼在较宽的攻角范围内的具有较大的升阻比,但最大升阻比比5%弦长襟翼模型稍小。5%与10%弦长的襟翼模型最大升阻比在攻角小于16°时均大于不带襟翼的模型;攻角大于16°时则正好相反。

图11 不同襟翼长度的模型升阻比曲线Fig.11 Lift drag ratio of airfoil with different length trailing edge flags
5 结 论
(1)通过两种翼型算例验证了尾缘襟翼向翼型压力面偏转,增大了翼型弯度,提高了翼型的升力系数。小攻角范围内,随着襟翼长度的增加,翼型的升力系数增大。当攻角较大时,翼型最大升力系数先随襟翼长度增加而增大,然后随襟翼长度增加,翼型升力系数开始下降。
(2)带襟翼的翼型模型阻力系数均大于不带襟翼的翼型阻力系数,且随着襟翼长度的增大,翼型阻力系数增大,在一定攻角范围升阻比也增大。
(3)翼型襟翼长度为10%弦长时,翼型在较宽的攻角范围内具有较大的升阻比,具有较好的综合气动性能。
[1] Abdelrahman A,Johnson D A.Development of a wind turbine test rig and rotor for trailing edge flap investigation:static flap angles case[C]//Journal of Physics:Conference Series.IOP Publishing,2014,524(1):2-3.
[2] Andersen P B,Henriksen L,Gaunaa M,et al.Deformable trailing edge flaps for modern megawatt wind turbine controllers using strain gauge sensors[J].Wind Energy,2010,13(2):193-206.
[3] Yu W,Zhang M M,Xu J Z.Effect of smart rotor control using a deformable trailing edge flap on load reduction under normal and extreme turbulence[J].Energies,2012,5(9):3608-3626.
[4] Castaignet D,Barlas T,Buhl T,et al.Full-scale test of trailing edge flaps on a Vestas V27wind turbine:active load reduction and system identification[J].Wind Energy,2014,17(4):549-564.
[5] Pastrikakis V A,Steijl R,Barakos G N,et al.Computational aeroelastic analysis of a hovering W3sokol blade with Gurney flap[J].Journal of Fluids and Structures,2015,53:96-111.
[6] Wang J J,Li Y C.The effects of Gurney flap on double delta wing aerodynamic performance in low speed wind-tunnel test[J].Acta Aerodynamica sinica,2007,25(2):216-219.(in Chinese)王晋军,李亚臣.Gurney襟翼对双三角翼气动特性影响的低速风洞实验研究[J].空气动力学学报,2007,25(2):216-219.
[7] Xiao T,Daichin.The experimental study of aerodynamics and flow structures of a wing with Gurney flaps in ground effect.Acta Aerodynamica sinica,2013,31(5):572-578.(in Chinese)肖涛,代钦.Gurney襟翼对机翼地面效应气动特性和流动结构的影响实验研究[J].空气动力学学报,2013,31(5):572-578.
[8] Karthikeyan N,Murugavel K K,Kumar S A,et al.Review of aerodynamic developments on small horizontal axis wind turbine blade[J].Renewable and Sustainable Energy Reviews,2015,42:801-822.
[9] Li R N,Yuan S K,Zhao Z Q.Research on the effect of trailedge improvement on airfoils performance for wind turbine[J].Acta Aerodynamica Sinica,2012,30(5):646-652.(in Chinese)李仁年,袁尚科,赵子琴.尾缘改型对风力机翼型性能的影响研究[J].空气动力学学报,2012,30(5):646-652.
[10]Zhang X,Li W,Xing J Z,et al.Effects of geometrical parameters of improved Gurney flap on airfoil aerodynamic characteristics[J].Transaction of the Chinese Society for Agricultural Machinery,2012,43(012):97:101.(in Chinese)张旭,李伟,邢静忠,等.改进Gurney襟翼几何参数对翼型气动特性的影响[J].农业机械学报,2012,43(012):97-101.
[11]Troldborg N.Computational study of the Ris-B1-18airfoil with a hinged flap providing variable trailing edge geometry[J].Wind Engineering,2005,29(2):89-114.
[12]Li C F,Xu Y,Xu J Z.Influence of slot on wind turbine airfoil with trailing edge flaps[J].Journal Engineering Thermophysics,2011,32(11):1851-1854.(in Chinese)李传峰,徐宇,徐建中.凹槽对风力机叶片尾缘襟翼性能的影响[J].工程热物理学报,2011,32(11):1851-1854.
[13]Van Dam C P,Nakafuji D Y,Bauer C,et al.Computational design and analysis of a microtab based aerodynamic loads control system for lifting surfaces[C]//Micromachining and Microfabrication.International Society for Optics and Photonics,2003:28-39.
[14]Wang R,Xia P Q.Control of helicopter rotor blade dynamic stall and hub vibration loads by multiple trailing edge flaps[J].Chinese Journal of Aeronautics,2013,34(5):1083-1091.(in Chinese)王荣,夏品奇.多片后缘小翼对直升机旋翼桨叶动态失速及桨毂振动载荷的控制[J].航空学报,2013,34(5):1083-1091.
[15]Lackner M A,van Kuik G.A comparison of smart rotor control approaches using trailing edge flaps and individual pitch control[J].Wind Energy,2010,13(2‐3):117-134.
[16]Han Z H,Jia Y L,Li H F,et al.Aerodynamic performance of discrete trailing edge flaps of wind turbine airfoil[J].Transactions of the Chinese Society of Agricultural Engineering,2014, 30(20):58-64.(in Chinese)韩中合,贾亚雷,李恒凡,等.风力机分离式尾缘襟翼气动性能[J].农业工程学报,2014,30(20):58-64.
[17]Li Y R,Li R N,Wang X Y,et al.Effects of the calculation models with different dimension on the aerodynamic performance prediction for wind turbine airfoil[J].Transaction of the Chinese Society for Agricultural Machinery,2011,42(2):115-119.(in Chinese)李银然,李仁年,王秀勇,等.计算模型维数对风力机翼型气动性能预测的影响[J].农业机械学报,2011,42(2):115-119.
[18]Hand M M,Simms D A,Fingersh L J,et al.Unsteady aerodynamics experiment phase VI:wind tunnel test configurations and available data campaigns[M].Colorado:National Renewable Energy Laboratory,2001.
[19]Somers D M.Design and experimental results of S809airfoils[M].Colorado:National Renewable Energy Laboratory,1989.
The effect of trailing edge flaps length on aerodynamics of wind turbine airfoil
Han Zhonghe1,Jia Yalei1,2,*,Li Hengfan1,Zhu Xiaoxun1,Dong Shuai1
(1.Key Lab of Condition Monitoring and Control for Power Plant Equipment Ministry of Education,North China Electric Power University,Baoding 071003,China;2.Hebei software institute,Baoding 071003,China)
The goal of the study was to investigate the effect of trailing edge flaps length on aerodynamics of wind turbine airfoil,airfoil S809and DU series airfoil were selected as research objects,and six kinds of flap length airfoil model were designed,have the same chord length of 1 000mm,and the same deflect angle of 10°,the gap between the flap and the main airfoil body was optimized to make the width of gap as even 1mm.The grids near the trailing edge are refined,and the grid independence is verified through the comparison of the calculated results with grid scales three,which a 148 000grid model was selected for further calculation.The k-ω two equation turbulence model for commercial software Fluent was used here to calculate the aerodynamics of the flap models at different attack angles,the streamline,pressure contour and pressure coefficient near border of airfoil were analyzed and compared.The result shows that the flaps length of airfoil with trailing edge flaps has great effect on the aerodynamic performance of the airfoil,not only the streamline near the flap is influenced but also the whole streamline near the airfoil are influenced.The lift coefficient of airfoil with flap is bigger than that of airfoil without flap,and the lift coefficient increases with the increasing of flap length.The drag coefficient of flap model is also bigger than that of airfoil without flap,and the drag coefficient of flap modelalso increases with the increasing of angle of attack.The lift to drag ratio is bigger than that of airfoil without flap at some range of angles of attack.
wind turbine airfoil;discrete trailing edge flaps;computational fluid dynamics;lift to drag ratio
V211.41;V211.3
:Adoi:10.7638/kqdlxxb-2015.0021
2015-02-10;
2015-07-31
国家自然科学基金(11302076);中央高校基本科研业务专项资金(2014XS80)
韩中合(1964-),男,河北衡水人,教授,博士生导师,研究方向为:热力设备状态监测与故障诊断、两相流计算与测量、叶轮机械CFD与优化设计研究.E-mail:han_zhonghe@163.com
贾亚雷*(1975-),男,河北博野人,副教授,博士研究生,主要研究方向为:风力机叶片设计及优化研究.E-mail:yalei_jia@163.com
韩中合,贾亚雷,李恒凡,等.尾缘襟翼长度对风力机翼型气动性能的影响[J].空气动力学学报,2015,33(6):835-842.
10.7638/kqdlxxb-2015.0021 Han Z H,Jia Y L,Li H F,et al.The effect of trailing edge flaps length on aerodynamics of wind turbine airfoil[J].Acta Aerodynamica Sinica,2015,33(6):835-842.
0258-1825(2015)06-0835-08
