地下水数值模拟计算与预测

郭 锐

(辽宁省水文局, 沈阳 110003)



地下水数值模拟计算与预测

郭 锐

(辽宁省水文局, 沈阳 110003)

为了保障阜新地下水的开采量能够满足阜新供水的需求，针对阜新凌河地下水状况进行了预测。以阜新凌河地下水源区为例，建立地下水流数学模型，运用该模型对地下水流系统进行预测。应用GMS软件，用有限差分法的MODFLOW程序进行求解。在1方案总计6.42万m3/d和2方案总计8.42万m3/d的开采情景下，分别预测2015年阜新凌河地下水状况。结果表明所建立的数学模型能够较为真实地刻画研究区地下水系统的特征，仿真性强。从而得出文中所提出的两种方案均可行。

凌河; 地下水; 数值模拟计算; 开采预测

大凌河是辽宁省沿渤海西部的河流，发源于建昌县，流经朝阳、北票、义县等市县，流域面积23 837 km2,河长397 km。流域97%的面积处于辽西低山丘陵区，荒山秃岭，水土流失严重，河流含沙量大，气候干旱，是辽宁省内严重的资源性缺水地区，且暴雨集中，洪水来时陡涨陡落。通过查阅相关资料得知[1]，研究区内的含水层主要有：全新统冲洪积砂砾石孔隙潜水含水层、上更新洪冲积砂砾石承压含水层和层状岩类裂隙水。

为了满足阜新市需水的要求，现需要对现有1号水源井渗渠进行改造，以增加1号水源井供水量；在义县铁路桥至锦阜高速公路桥之间新建2处水源井，其中一处拟在铁路下游600 m新建2水源、另一处在锦阜高速公路桥上游550 m新建3水源，新建及改造的水源达到满足向凌河水源一泵站供水条件要求，供水能力达到6万m3/d。为了保障地下水开采量的可行性，需要对凌河地下水状况进行预测。

1 水文地质概念模型

水文地质概念模型是根据建模的目的，简化实际水文地质条件并组织相关数据，以便能够分析地下水系统，为建立地下水流数值模型提供依据[2]。通过对研究区水文地质条件的概化，确定模型的范围和边界条件、水文地质结构、地下水流场、水文地质参数与源汇项，为建立地下水数值模型奠定基础。本次数值模拟采用GMS软件，用有限差分法的MODFLOW程序求解。

1.1 研究区范围

研究区位于义县大凌河河谷平原区,北侧西起万佛堂以东、经双台子—头沟屯—红墙子—平房子、东至星星屯；南侧西起四方台、经前五里南—八家子、东至西地沟，东西长约18.5 km、南北长约8 km；为一个完整的河谷平原水文地质单元，面积122 km2。

1.2 含水层结构概化

根据区内水文地质调查情况，第四系含水层为研究对象，第四系厚度3～14 m，研究区地下水总的径流方向是沿着大凌河方向自西向东。地下水在多孔介质中的流动符合质量守恒定律和达西定律；本次模拟只考虑上层第四系含水层，忽略垂向水量交换，故将该区地下水运动概化为平面二维流；由于介质的非均匀性造成水文地质参数随空间变化，体现了系统的非均质性，因而可概化为非均质、各向同性含水层。因此将评价区含水系统概化为非均质各向同性、平面二维非稳定流地下水模型。

1.3 研究区边界条件概化

垂向边界：上部边界为潜水面，是位置不断变化的水量交换边界，有降水入渗和人工开采等；下部以白垩纪砂岩作为隔水底板，概化为隔水边界。

侧向边界：AB，EF为大凌河河谷平原区边界，概化为定流量边界，AB边界接受研究区外的地下潜流，为入流边界，研究区范围内地下水经过EF边界，以地下潜流形式排出研究区，EF为出流边界；CD，GH，IJ为支流河谷平原与大凌河干流河谷平原交接处，概化为定流量边界，均为入流边界；BC，DE，FG，JA为第四系地层与山区基岩交界处，概化为零流量边界(表1)。

表1 研究区边界条件

2 地下水流数学模型及求解

2.1 地下水流数学模型

根据水文地质概念模型，将研究区地下水流系统概化为非均质、各向同性、二维、潜水非稳定地下水流系统[3]，运用式(1) 进行计算：

(1)

式中：H0——水头初始值(m)；∂——第一类边界Γ1上的已知函数；q——第二类边界Γ2上的单位宽度侧向径流量(m2/d)；n——边界Γ2的外法线方向；T——导水系数(m/d)；S——贮水系数；w——单位时间在垂向从单位体积含水层中流入或流出的水量(m3)，包括，降水入渗补给地下水量和位于相应单元的抽、水量。

2.2 数学模型的求解

本次地下水数值模拟采用了当前国际上利用较广的GMS软件。GMS(Groundwater Modeling System)是美国Brigham Young大学环境模拟研究实验室开发的先进的、基于概念模型的地下水环境模拟软件。GMS全面包括了模拟地下水流每一个阶段所需的工具，如边界概化、建模、后处理、调参、可视化[4]。

运用基于有限差分法的modflow程序求解以上微分方程的定解问题。根据评价区水文地质结构和源汇项的特征，选择MODFLOW中相应的子程序包来实现地下水流的模拟。

2.3 空间离散

计算区面积为122 km2，利用GMS的3 D GRID模块实现网格剖分。共剖分矩形网格单元2 684个，每个单元个面积195 m×235 m。模拟期为2011年1月1日—2012年4月30日，以1天为1个应力期，1天1个时间步长。2012年5月1日—2015年12月31日为预测期，1个月为1个应力期，1天1个时间步长。初始水位流场采用1月1日水文观测数据，对比流场采用4月20日实测值。

2.4 水文地质参数分区及初值的确定

用于地下水流模型的水文地质参数主要有两类，一类是用于计算各种地下水补排量的参数和经验系数，如大气降水入渗系数；另一类是含水层的水文地质参数，主要包括潜水含水层的渗透系数和给水度[5]。

本次计算所采用的参数有渗透系数、给水度、降水入渗系数等参数，主要是根据区内勘察和现有资料确定，根据参数分布规律和渗流场特征，对各项参数进行分区。

降水入渗系数的大小与包气带岩性、地下水埋深、降水量、降水强度、降水前土壤含水量、地形地貌、地面植被等因素有关[6]，前两者起主导作用。通过对这些因素分析，将研究区分为4个降水入渗分区。分区2为大凌河河漫滩地段，地下水埋深浅、地表岩性粗降水入渗系数稍大，取值0.25～0.3；分区1与分区3为河流阶地降水入渗系数较分区1稍小，分区1地面坡度较分区3大，因此分区3降水入渗系数取值较分区1稍大，分区1系数取值0.18～0.22，分区3取值0.2～0.25；分区4为义县县城范围，为硬覆盖区，降水入渗系数最小，取值0.15～0.18。

渗透系数与给水度是通过抽水试验资料计算得到，参考已有评价结果[7]，结合各种岩性的经验渗透系数值，综合确定各计算分区渗透系数及给水度的大致取值范围。

表2 渗透系数与给水度初值

2.5 研究区源汇项的确定

研究区孔隙含水层主要接受河道渗漏补给、地下径流侧向补给、降水入渗补给[8]；地下水主要消耗于人工开采和地下水侧向径流排泄，由于研究区潜水蒸发微弱，忽略潜水蒸发量计算。

1) 河流渗漏补给量。天然条件下，河流侧向补给量随年份和丰枯季节变化。在模型处理时将其概化为RⅣER边界，水位根据义县水位站监测数据差值确定，模型RⅣER模块自动计算地表水与地下水的水力联系强度，河流渗漏补给量采用达西定律由模型自动识别计算。

2) 地下水侧向补给量。根据达西定律，各个流量边界段侧向径流量按如下公式计算：

Qc=K·I·B·M·ΔT

(2)

式中：Qc——地下水侧向径流量(104m3/a)；K——含水层渗透系数(m/d)；I——水力坡度；B——断面宽度(m)；M——含水层厚度(m)；ΔT——计算时间(d)。

根据公式(2)，依据动态观测资料确定边界流量随时间段的变化趋势，根据不同时期流场选取各段的水力梯度，根据给定的水文地质参数初值，计算给定随时间变化的侧向补给(排泄)量。

3) 降水入渗补给量：降水入渗补给是本区地下水的重要补给源，其入渗量与降水量、潜水水位埋深和包气带岩性有关。降水入渗补给量的计算采用公式：

pr=p·α·F×10-1

(3)

式中：pr——降水入渗补给量(万m3)；p——降水量(mm)；α——降水入渗补给系数(无因次)；F——计算区计算面积(km2)。

模型中，以日降水量按照不同分区，不同降水入渗系数以Recharge的形式面状补给地下水。

4) 地下水开采量：扣除丰安用水80万m3/a,合计取水1 525.1万m3/a，折成日量为41 784 m3/d。

5) 地下水侧向排泄量：计算方法同地下水侧向补给量。

6) 水位、降水量采用义县水文站数据。

2.6 数学模型的识别和验证

由于对目的层的水文地质条件有比较清楚的认识，各水文地质参数初值范围也比较客观，通过细致的调参拟合，模型识别取得了较好的结果，参数识别结果见下表。计算流场与识别流场基本相同。

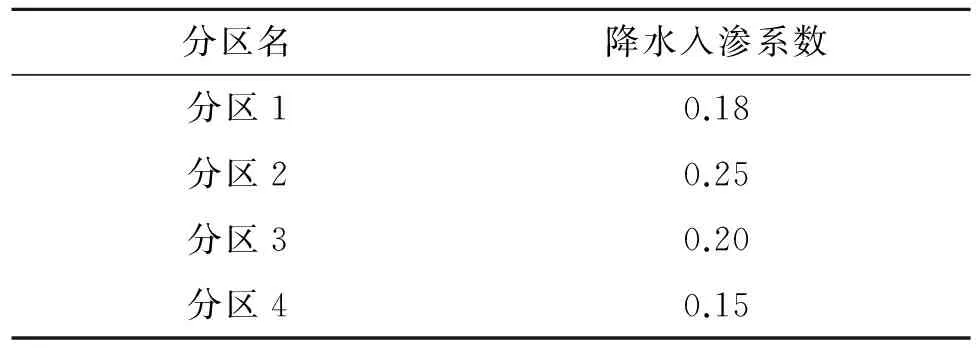
表3 降水入渗系数识别结果

表4 渗透系数与给水度识别结果

2.7 模拟计算区地下水可动用的储存量的计算

按照区域水文地质条件，模拟计算区含水层厚度一般为3～5 m，计算分区给水度在0.08～0.18之间，模拟计算区面积为122 km2，用以下公式进行计算：

W=1/3×h×μ×F

(4)

式中：W——地下水可动用的储存量(m3)；h——地下水面以下含水层厚度(m)；μ——区域给水度；F——计算面积(m2)。

含水层厚度采用4 m，给水度采用0.16，计算得模拟计算区地下水可动用的储存量为2 603万m3。

2.8 地下水状况预测

由于研究区渗透系数较大，水源区开采主要是袭夺地表径流量，河道水是控制研究区地下水可开采量的主要因素，在义县站95%水位(59.42 m)保证率下，按连续枯水年降雨情况对水源井不同开采条件下，对研究区地下水状况进行预测。

2.8.1 地下水状况预测开采1方案 现状3，4号井关闭,现状2号井开采0.42万m3/d、改1井开采1.4万m3/d、新2井1.9万m3/d、新3井2.7万m3/d，总计6.42万m3/d的开采情景下，预测2015年研究区地下水状况。

按照预报方案采用非稳定流模型进行模型模拟，可以得出研究区2015年汛期与非汛期地下水流场演变趋势。在方案1条件下，研究区范围内，在新3井与现2井附近形成了漏斗区，但是漏斗区面积很小，汛期(6—9月)0.2 km2，漏斗最大直径585 m，非汛期(10—4月)0.24 km2漏斗最大直径780 m，降深小于1.0 m，说明新井开采对研究区地下水动态的影响不大。整体上枯水期地下水水位较丰水期略有下降，但是下降不明显，说明降水不是研究区地下水的主要补给源，侧向入流与河道渗漏控制着研究区的地下水补给。

在方案1条件下，汛期河道渗漏量78 441 m3/d，占总开采量的74.0%，需袭夺河水0.908 m3/s。非汛期河道渗漏量91 011 m3/d；占总开采量的85.9%，需袭夺河水1.053 m3/d。年内水均衡量为-1 979 m3/d，为负均衡，年均衡量为72.2万m3，可见区内补给量小于消耗量，需动用储存量(按可动用储存量的60%计算)，年均衡量仅占可动用储量的4.6%。可见区内水源地取水6.42万m3/d是可行的。

2.8.2 地下水状况预测开采2方案 新建2，3号井与改1号井以设计流量开采，即，改1井开采量1.4万m3/d、新2井1.9万m3/d、新3井2.7万m3/d、现状2号井开采量0.42万m3/d，现状3，4号井以原有开采量1半开采，即：现3井开采1.2万m3/d、现4井0.8万m3/d。总计8.42万m3/d的开采情景下，2015年研究区地下水状况。

按照预报方案采用非稳定流模型进行模型模拟，可以得出研究区2015年汛期与非汛期地下水流场演变趋势。在方案2条件下，新3号井与现2井范围形成漏斗，漏斗面积汛期(6—9月)0.18 km2，漏斗最大直径580 m，非汛期(10—4月)为0.33 km2，漏斗最大直径877 m，降深小于1.0 m；现3井附近虽然没有形成闭合漏斗，但是开采区降深加大，有形成漏斗的趋势。整体上枯水期地下水水位较汛期略有下降，但是下降不明显。

汛期河道渗漏量84 561 m3/d，占地下水实际开采量67.1%,需袭夺河水0.979 m3/s；非汛期河道渗漏量99 313 m3/d，占地下水实际开采量78.8%，需袭夺河水1.149 m3/s。年内水均衡量为-2 981 m3/d，为负均衡，年均衡量为108.8万m3，可见区内补给量小于消耗量，需动用储存量，年均衡量占可动用储量的4.2%。可见区内水源地取水8.42万m3/d是可行的。

3 结 论

通过对地下水计算流场和流场的拟合统计分析，说明含水层结构、边界条件概化、水文地质参数的选取及源汇项的选取的是合理的，所建立的数学模型较为真实地刻画了研究区地下水系统的特征，仿真性强，可以运用该模型进行地下水流系统的预测。

本文为了保障阜新地下水的开采量能够满足阜新供水的需求，针对阜新凌河地下水状况进行了预测。由于研究区渗透系数较大，水源区开采主要是袭夺地表径流量，河道水是控制研究区地下水可开采量的主要因素，在义县站95%水位(59.42 m)保证率下，按连续枯水年降雨情况对水源井不同开采条件下，对阜新凌河2015年地下水状况进行预测，从而得出两方案可见区内水源地取水6.42万m3/d和可见区内水源地取水8.42万m3/d均是可行的。

[1] 贾金生,田冰,刘昌明.Visual MODFLOW在地下水模拟中的应用[J].河北农业大学学报,2003,26(2):71-78.

[2] 马驰,石辉,卢玉东.MODFLOW在西北地区地下水资源评价中的应用[J].干旱区资源与环境,2006(2):89-93.

[3] 丁元芳,迟宝明,易树平,等.Visual MODFLOW在李官堡水源地水流模拟中的应用[J].水土保持研究,2006,13(5):99-102.

[4] 王金生,王长申,滕彦国.地下水可持续开采量评价方法综述[J].水利学报,2006,37(5):525-533.

[5] 李勤奋,方正.上海市地下水可开采量模型计算及预测[J].上海地质,2000(2):36-43.

[6] 魏鸿.开封市地下水资源供求预测研究[J].地下水,2001,23(4):168-169.

[7] 赵凤双.地下水开采量与可开采量探析[J].农业与技术,2008,27(5):97-97.

[8] 师幸生.太原市地下水开采量控制目标探讨[J].山西水利,2008,24(4):21-23.

Numerical Simulation and Prediction of Groundwater Sources

GUO Rui

(HydrologicalBureauofLiaoningProvince,Shenyang110003,China)

In order to guarantee the quantity of groundwater exploitation to meet the demand for the water rsupply of Fuxin, Ling River groundwater condition in Fuxin was predicted. Groundwater source area of Ling River was set as an example, a groundwater flow model was used to predict groundwater flow system. It was solved using the finite difference method modflow program of applying GMS software. Under a programs of 64 200 m3/d and the program of 84 200 m3/d mining scenarios groundwater conditions of Ling River in Fuxin were predicted in 2015. The results show that the mathematical model can more realistically describe the characteristics of groundwater systems, and the simulation is strong. We can come to a conclusion that the proposed two schemes are feasible based on the prediction results.

Ling River; groundwater; numerical simulation; mining prediction

2014-04-21

2014-06-06

国家自然科学基金重点项目(50979012)

郭锐(1983—),女(满族),辽宁沈阳人,硕士,中级工程师,研究方向:主要从事水资源方向的研究。E-mail:65893242@qq.com

TV211.1

1005-3409(2015)02-0295-04