基于近似熵理论的三江平原月降水量空间复杂性分析

付 强, 李铁男, 李天霄, 孟凡香

(1.东北农业大学 水利与建筑学院, 哈尔滨 150030;2.黑龙江省粮食产能提升协同创新中心, 哈尔滨 150030; 3.黑龙江农垦勘测设计研究院, 哈尔滨 150030)



基于近似熵理论的三江平原月降水量空间复杂性分析

付 强1,2, 李铁男1, 李天霄1, 孟凡香3

(1.东北农业大学 水利与建筑学院, 哈尔滨 150030;2.黑龙江省粮食产能提升协同创新中心, 哈尔滨 150030; 3.黑龙江农垦勘测设计研究院, 哈尔滨 150030)

以三江平原7个国家级气象站1959—2013年的月降水量数据为基础，采用近似熵理论、ArcGIS空间分析理论，分析了近50 a三江平原月降水量的空间复杂性。结果表明：三江平原月降水量表现出了较强的非线性特征，其中南部鸡西站月降水量的极差最大，达到了340.1 mm，北部富锦站月降水量的极差最小，仅为231.6 mm；月降水量空间复杂性东西方向整体呈现出了条状分布，且由西南向东北逐渐增加，这主要与三江平原西南部海拔低，湿地面积多，降水日数与降水强度小，且多为山区等因素有关。研究成果对于指导三江平原科学合理地利用降水资源具有一定的指导意义。

三江平原; 近似熵理论; 月降水量; 空间复杂性

降水系统是一个涉及地形地貌、气象变化等众多因素的复杂非线性系统，由于其各影响因素自身的非线性、不确定性，使得降水的变化呈现出了貌似随机却非随机的特征，导致传统方法在研究降水复杂性变化规律时遇到了很大的困难[1]。而降水是形成地表径流，补充地表水的主要来源，与人类的生活有着密切的联系[2]，降水过程的非线性、不确定性和混沌性为人类开发利用大自然带来了诸多不便，产生了一系列干旱、洪涝等自然灾害。另外，三江平原作为我国重要的商品粮生产基地，由于受温带湿润、半湿润大陆性季风气候的影响，降水年内分配不均，年际变化幅度大，汛期降水占全年降水的70%以上，冬春季节降水较少，而6—8月份降水强度较大，洪涝灾害比较严重。同时，由于近几年来人们对三江平原开发力度的加大，气候变化更加突出，使得降水系统表现出越来越多的非线性、随机等复杂性特征，严重威胁着三江平原水资源的可持续利用和社会经济的可持续发展。同时，按照2013年8月国务院批复的《黑龙江省“两大平原”现代农业综合配套改革试验涉农资金整合方案》，黑龙江省将在未来三年内将三江平原建成我国商品粮生产基地的核心区。因此，研究三江平原降水系统的复杂性特征，进而有效利用雨水资源，科学合理地开发地表水资源对于解决三江平原存在的诸多水资源问题具有重要的理论和实践意义。

目前，研究水文系统复杂性的方法主要有混沌理论[2-3]、等概率粗粒化LZC算法[4]、分维分形理论[5]、Lyapunov指数[6]等，其中，混沌理论、Lyapunov指数计算结果不够稳定，等概率粗粒化LZC算法和分维分形理论计算理论和方法较为复杂，导致计算结果难以充分揭示水文序列的复杂性特征。近似熵理论是由Pincus于1991年提出的，由于其具有所需计算数据短、抗噪声能力强、对数据是否随机的依赖性小等优势[7]，目前已被广泛应用于地下水[7-8]、径流[9]及气候突变监测[10]等相关领域的系统复杂性分析中，但在降水系统复杂性特征分析方面应用的相对较少。为此，本文采用近似熵理论分析三江平原月降水量的复杂性特征，同时结合GIS的空间分析功能对月降水量复杂性的空间分布特征进行识别。

1 数据来源及方法

1.1 研究区域

三江平原是由黑龙江、乌苏里江和松花江三条大江汇流、冲积而成的低平沃土，位于黑龙江省东部，43°49′—48°27′N，129°11′—35°05′E[11-12]，北起黑龙江、南抵兴凯湖、西邻小兴安岭、东至乌苏里江，总面积约10.89万km2，湿地面积约为2.4万km2，总人口862.5万人，是我国重要的商品粮生产基地，每年为国家提供20%的商品粮，对保障我国粮食安全具有重要的作用。

1.2 近似熵理论

近似熵是用一个非负数来表示一个时间序列的复杂性，ApEn值越大，表明时间序列越复杂。设某随机时间序列数据为x(1)，x(2)，…，x(n)，共n个数据[7,9]，

(1) 按序号连续顺序组成一组m维矢量：

X(i)=[x(i)，x(i+1)，…，x(i+m-1)]

(i=1，…，n-m+1)

(1)

(2) 计算矢量X(i)与X(j)的欧氏距离为：

(2)

(3)

(4)

(6) 理论上此序列的近似熵为：

(5)

一般来说，该极限以概率1存在。实际水文时间序列长度n不可能为∞。当n为有限值时按上述步骤得出的是序列ApEn的估计值，记为：

ApEn(m，r，n)=φm(r)-φm+1(r)

(6)

显然，ApEn的大小与m和r的取值有关。Pincus建议，实践中可取m=2，r=kσx[k=0.1～0.25σx]，σx为原始随机时间序列x(i)(i=1，…，n)的标准差。

由前述分析步骤可知：近似熵值反映了重构序列在m维条件下的自相似程度，熵值越大，其产生新模式的概率就越大，所对应的降水系统就越复杂。同时，近似熵理论并不完全依靠重构吸引子，所以对降水系统这种非线性时间序列具有很好的适用性[13]。

1.3 数据来源

本研究采用的数据来源于中国气象科学数据共享服务网(http:∥www.cma.gov.cn/2011 qxfw/2011qsjgx/)，包括7个国家级气象站的月降水量。由于鹤岗站部分数据缺失，其数据系列长度与其他6个站有所不同。所选的7个气象站在空间上覆盖了三江平原的大部分区域，各气象站点具体信息和数据序列长度如表1所示。同时，为了避免本文数据因观测和记录所存在的误差，对所获取的数据采用图解法进行一致性检验，并采用统计法进行校核[14]，所有数据均通过了置信水平为95%的检验，可以满足分析需要。

2 结果与分析

采用三江平原7个国家级气象站的数据绘制月降水量变化曲线，如图1所示。从图1中可以看出，1959—2013年，随着高强度农业开发活动对生态环境的影响，三江平原7个国家级气象站的月降水量均表现出了较强的非线性特征，其中南部鸡西站月降水量的极差最大，达到了340.1 mm，北部富锦站月降水量的极差最小，仅为231.6 mm，比鸡西站少了近100 mm，可见三江平原月降水量空间分布存在较大差异。

表1 三江平原气象站信息

图1 1959-2013年三江平原七个国家级气象站月降水量变化曲线

2.1 三江平原月降水量序列复杂性测度

选取维数m=2，k=[0，1]，分析k值对三江平原月降水量序列近似熵值的影响，如图2所示。从图2中可以看出，当k值较小时，随着k值的增加，ApEn值逐渐增大，达到最大值后，随着k值的增加开始逐渐减小。在0.23附近，ApEn值达到最大值，且各气象站月降水量ApEn值的分辨效果最好。整体上，各站月降水量的ApEn值均呈现出了先增加后减小的下抛物线波动特征。为了进一步揭示k值对三江平原月降水量复杂性的影响，绘制月降水量近似熵值变幅随k值的变化曲线，如图3所示。从图3中可以看出，随着k值的增加，ApEn值变幅值与ApEn值的变化规律正好相反，呈现出了先减小后增大的上抛物线特征，且在0.23附近，各站月降水量的ApEn值变幅值相差最小，均在3%以内。故可以认为此时月降水量复杂性计算结果已经趋于稳定，因此，取k=0.23，即：r=0.23σx。

图2 三江平原月降水量近似熵值随k的变化曲线

采用ApEn(2，0.23σx)对三江平原7个国家级气象站的月降水量序列的复杂性进行排序，三江平原月降水量序列的复杂性排序为：虎林>宝清>富锦>依兰>鸡西>佳木斯>鹤岗。从空间角度分析可知：三江平原月降水量序列复杂性呈现出了东北部比西南部复杂的特征。

图3 三江平原月降水量近似熵值变幅曲线

2.2 三江平原月降水量空间复杂性特征及成因分析

为了进一步揭示三江平原月降水量复杂性在空间上的分布规律，采用ArcGIS地统计分析模块中的普通克里格插值法[15-16]，空间分辨率设置为500 m，变异函数采用球形模型，对三江平原月降水量复杂性进行空间识别，空间分析结果如图4所示。从图4中可以看出：三江平原月降水量空间复杂性东西呈现出条状分布，且由西南向东北逐渐增加。说明三江平原东北部月降水量序列的影响因子较多，不确定成分比较复杂，彼此之间相互影响，造成了其降水系统结构复杂性较强。而西南部月降水量的影响因子对其的影响相对较小，彼此之间影响比较薄弱，导致其降水系统结构复杂性相对较弱。

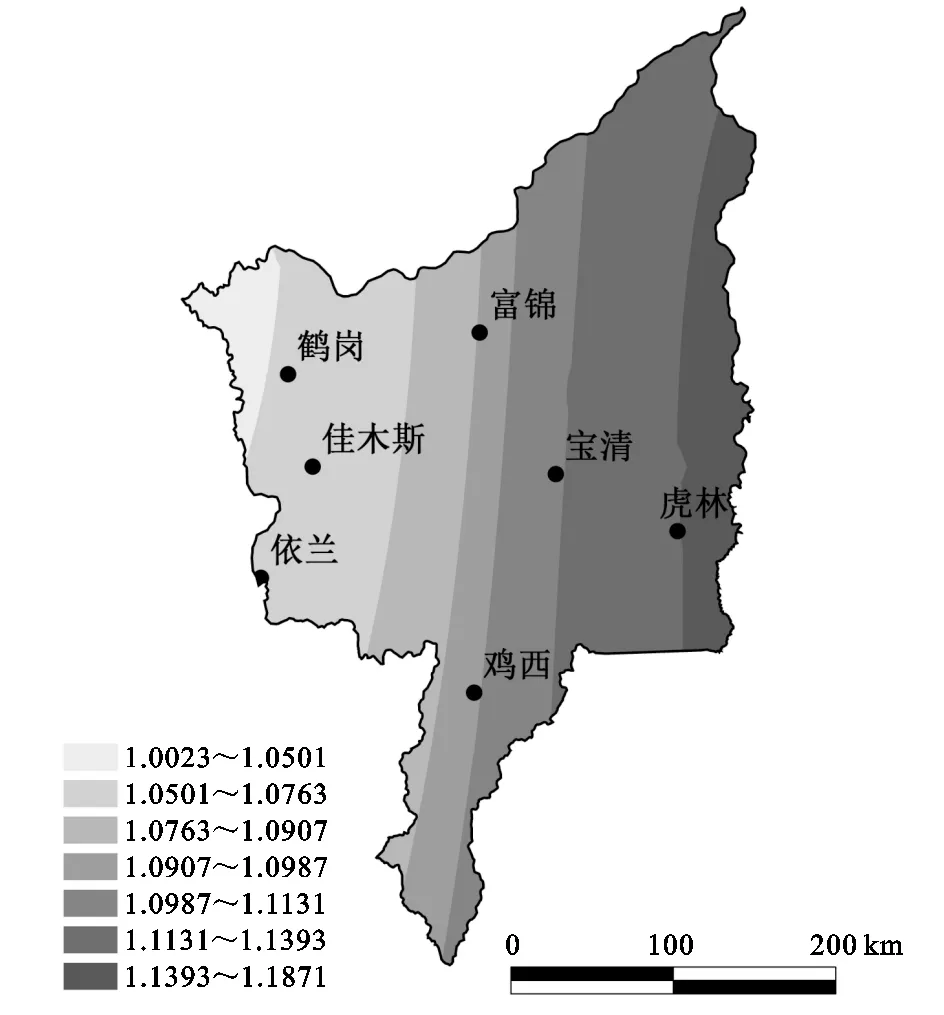
图4 三江平原月降水量空间复杂性分布

造成三江平原月降水量空间复杂性差异的原因可能与水系组成、海拔、气温、下垫面条件等水文地质条件等因素有关。一方面，三江平原地势低平，整体上由西南向东北倾斜，因此，由东北向西南随着海拔高度的逐渐增加，降水日数与降水强度逐渐增大，促进了降水序列季节性不均匀分布的几率。同时，三江平原东北水系比较发达，而西南多为山区，这在一定程度上导致了三江平原东北部蒸发、气温等气象因素变幅比西南剧烈，促进了降水序列的不均匀分布。另一方面，三江平原西南部湿地面积较多，几乎是东北部的一倍。湿地能够涵养水源，影响小气候，降低各气象因子的变化幅度，进而在一定程度上也促使了西南部降水系统结构复杂性比东北部弱。

3 结 论

(1) 近似熵理论所需数据量短、所需参数较少、且抗干扰和抗随机性能力较强，其计算结果较好地反映了降水序列的复杂性特征，为分析水文序列复杂性特征提供了一种研究思路。

(2) 三江平原月降水量表现出了较强的非线性特征，其中南部鸡西站月降水量的极差最大，达到了340.1 mm，北部富锦站月降水量的极差最小，仅为231.6 mm，比鸡西站少了近100 mm。

(3) 三江平原月降水量序列的复杂性排序为：虎林>宝清>富锦>依兰>鸡西>佳木斯>鹤岗。东西方向整体呈现出条状分布，且由西南向东北逐渐增加。

(4) 三江平原西南部海拔低，湿地面积多，降水日数与降水强度小，且多为山区，在一定程度上也促使了西南部降水系统结构复杂性比东北部弱。

[1] 刘卫林.漳河观台站降雨径流时间序列的混沌特性分析[J].河海大学学报:自然科学版,2011,39(4):384-390.

[2] 于延胜,陈兴伟.福州市区降雨序列多时间尺度的混沌特征[J].福建师范大学学报:自然科学版,2008,24(5):96-100.

[3] Millan H, Rodriguez J, Ghanbarian-Alavijeh B, et al. Temporal complexity of daily precipitation records from different atmospheric environments:Chaotic and Levy stable parameters[J]. Atmospheric Research,2011,101(4):879-892.

[4] 武秋晨,刘东.等概率粗粒化LZC算法在降水变化复杂性研究中的应用[J].中国农村水利水电,2013(5):1-5,10.

[5] 刘东,张健,付强.基于连续小波变换与分形理论的三江平原井灌区地下水埋深序列复杂性研究[J].水土保持研究,2011,18(2):116-120.

[6] Fan Q, Wang Y, Zhu L. Complexity analysis of spatial-temporal precipitation system by PCA and SDLE[J]. Applied Mathematical Modelling,2013,37(6):4059-4066.

[7] 刘东,周明,孟军.近似熵在三江平原地下水埋深序列复杂性分析中的应用[J].自然资源学报,2012,27(1):115-121.

[8] 刘萌,刘东.基于样本熵的地下水埋深序列复杂性分析[J].水利水电技术,2012,43(12):5-8.

[9] 孙东永,黄强,王义民,等.滑动近似熵在径流序列突变性分析中的应用[J].水力发电学报,2014,33(4):1-6.

[10] 王启光,张增平.近似熵检测气候突变的研究[J].物理学报,2008,57(3):1976-1983.

[11] Pan X, Yan B, Yoh M, et al. Temporal variability of iron concentrations and fractions in wetland waters in Sanjiang Plain, Northeast China[J]. Journal of Environmental Sciences-China,2010,22(7):968-974.

[12] Zhou D, Gong H, Wang Y, et al. Driving forces for the marsh wetland degradation in the Honghe National Nature Reserve in Sanjiang Plain, Northeast China[J]. Environmental Modeling & Assessment,2009,14(1):101-111.

[13] 何文平,何涛,成海英,等.基于近似熵的突变检测新方法[J].物理学报,2011,60(4):820-828.

[14] 原立峰,张增信,刘星飞,等.鄱阳湖流域近49a降雨序列一致性检验与分析[J].安徽农业科学,2013,41(2):732-735.

[15] 姜秋香,付强,王子龙.空间变异理论在土壤特性分析中的应用研究进展[J].水土保持研究,2008,15(1):250-253.

[16] 腊贵晓,顾怀胜,刘国顺,等.喀斯特地区烟田土壤养分的空间变异特征[J].水土保持研究,2012,19(3):48-53.

Analysis of Spatial Complexity of Monthly Precipitation in Sanjiang Plain Based on Approximate Entropy

FU Qiang1,2, LI Tienan1, LI Tianxiao1, MENG Fanxiang3

(1.CollageofWaterConservancy&Architecture,NortheastAgriculturalUniversity,Harbin150030,China; 2.CollaborativeInnovationCentreofGrainProductionPromotioninHeilongjiangProvince,Harbin150030,China; 3.HeilongjiangNongkenSurveyDesignResearchInstitute,Harbin150090,China)

The approximate entropy theory and ArcGIS spatial analysis theory were used to analyze the spatial complexity of monthly precipitation data collected at seven national weather stations in the Sanjiang Plain from 1959 to 2013. The results showed that the monthly precipitation presented a strong nonlinear feature. The range of monthly precipitation in Jixi station was maximum, which reached to 340.1 mm, and it was minimum in Fujin station, which only reached to 231.6 mm. The spatial complexity of monthly precipitation presented a strip distribution at the east-west direction and increased gradually from the southwest to northeast. The low altitude, more wetland and mountain areas, small precipitation intensity and precipitation day were the main drivers of difference in the spatial complexity characteristics. The research results can provide guidance for scientific investigations and the reasonable use of rainfall resources in the Sanjiang Plain.

Sanjiang Plain; approximate entropy theory; monthly precipitation; spatial complexity

2014-10-02

2014-11-10

国家自然科学基金(51179032,51479032);水利部公益性行业科研专项经费项目(201301096);教育部新世纪优秀人才支持计划;黑龙江省高校长江学者后备支持计划项目;黑龙江省杰出青年基金(JC201402)

付强(1973—),男,辽宁锦州人,教授,博士生导师,主要从事农业水土资源系统分析、节水灌溉及农业系统工程建模与优化技术、冻融土壤水热作用机理等方面研究。E-mail:fuqiang0629@126.com

P333.1;S11+

A 文章编号：1005-3409(2015)02-0113-04