电压间谐波对紧凑型荧光灯光闪变效应的实验研究

雍 静 晏小龙 曾礼强

电压间谐波对紧凑型荧光灯光闪变效应的实验研究

雍 静 晏小龙 曾礼强

（重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400030）

为进行实验研究，对 IEC闪变仪模型中的加权滤波器进行分解，提出闪变仪的分解模型，该模型可直接导入实验获得的光通量信号以进行光闪变强度Pst计算，实验验证了该模型的可行性和有效性；设计并建立了实验装置，利用高准确度照度计采集紧凑型荧光灯在含有特定间谐波频率和幅值的电压下的光通量输出，使用闪变仪分解模型，对其在间谐波电压下的光闪变效应进行实验研究，获得了紧凑型荧光灯在不同间谐波频率和含量下的光闪变强度 Pst，并据此提出了针对紧凑型荧光灯光闪变的间谐波限制曲线。

间谐波 闪变仪 光通量 闪变 间谐波限制曲线

1 引言

随着电力电子技术的迅速发展，各种电力电子装置的广泛应用，大量谐波、间谐波给电力系统带来诸多电能质量问题。其中，变频调速设备的大量使用使间谐波问题越来越受到重视[1-2]。间谐波会带来电压波动，形成电压闪变效应[3-4]，引起照明光源光通量波动，导致光闪变效应[5-7]。迄今为止，学者们对含间谐波电压的波动特征[8]，间谐波闪变效应的计算与评估[9-10]等进行了研究，取得一定成果。

目前国际上较通行的光闪变研究及测试标准是IEC闪变仪，它基于调幅电压对白炽灯的闪变效应设计[11]，但对于评价间谐波给荧光灯造成的闪变效应具有很大的局限性[12-15]。一方面，相比于调幅电压波动，间谐波的出现越来越广泛，而 IEC闪变仪无法对高频间谐波引起的闪变效应作准确评价[12-13,19-21]；另一方面，IEC 闪变仪中的滤波器是以白炽灯作为评价对象设计，调幅电压波动限制值也是针对白炽灯得出，荧光灯与白炽灯工作原理不同，闪变机理也不同，因此IEC闪变仪以及相关闪变限制值对间谐波导致的荧光灯闪变不再适用[14-15]。有必要对荧光灯在间谐波下的光闪变效应进行研究。

文献[15-18]对于荧光灯光闪变效应进行了初步的理论研究，但由于荧光灯工作过程的复杂性，电路的非线性和多样性等因素，尚未形成基本的理论研究成果[22]，关于间谐波条件下的荧光灯闪变实验研究也较少，缺乏荧光灯闪变的间谐波兼容水平。

紧凑型荧光灯是目前用于替代白炽灯的一种荧光灯型，使用范围广泛。本文针对紧凑型荧光灯进行光闪变实验研究，以期获得针对其光闪变的间谐波限制曲线。主要方法是：对IEC闪变仪模型进行分解，提出能将光通量信号直接导入的闪变仪分解模型，该分解模型保留了IEC闪变仪分析人眼和大脑对于光通量波动效应的部分，利用其进行光闪变强度计算；采集不同的间谐波电压条件下的荧光灯光通量信号，利用分解模型计算其短时光闪变强度Pst，获得 Pst=1时的间谐波含量限制值，提出间谐波闪变限制曲线。这种方法可以推广到其他光源，并获得相应的间谐波限制曲线，可为制订电力系统间谐波限制标准提供依据。

2 IEC闪变仪原理及分解模型

2.1 IEC闪变仪的原理

IEC闪变仪由五个模块组成[11]。如图 1所示。图中，模块 1为采集电压信号 v(t)，并将其作归一化处理，得到电压标幺化信号 v0(t)。模块 2为对归一化电压信号作平方处理得 v02(t)，得到电压的波动状况。模块3为加权滤波环节，由两个级联的滤波模块组成：模块3-1和模块3-2。模块3-1为带通滤波器（0.05～35/42Hz）。对模块 2输出的电压平方信号滤波，目的是提取调幅电压的低频有效值波动信号dv(t)，并以此作为评价人对灯的闪变感受的依据；模块3-2为中心频率为8.8Hz的加权滤波器。模拟灯-眼的工作过程，输出人眼对波动电压导致的白炽灯光通量波动的视觉反应信号 eye(t)。该模块由白炽灯型式、电压、功率以及人的年龄、身体状况等因素决定。可以把该模块看作灯与眼两个环节，分解为两个模块[23]，如图2所示。其中，模块3-21模拟灯的行为，由输入电压波动信号dv(t)，得到灯输出的光通量波动信号dLum(t)，该部分只与灯参数相关；模块 3-22模拟人眼的行为，由输入的光通量波动信号，得到人眼视觉反应信号，这个环节只与人眼的工作机理有关。模块4由平方环节和平滑环节组成，模拟人脑对眼睛接受光刺激的反应，输出人脑对光闪变的感受信号 brain(t)。模块 5为评价指标的统计算法，输出评价结果，常用 1min短期闪变强度值Pst作为光源是否发生闪变的判定标准。

图1 IEC闪变仪原理框图Fig.1 Block diagram of IEC flickermeter

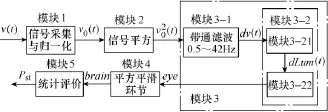
图2 IEC闪变仪原理框图分解模型Fig.2 Block diagram decomposition of IEC flickermeter

2.2 闪变仪的分解模型

IEC的闪变仪标准中的输入电压为调幅电压，对于额定电压为120V/60Hz与230V/50Hz的两种白炽灯，分别在输入电压为正弦与矩形两种调幅电压形式时，给出了在短时闪变评价值 Pst=1时不同频率调幅电压的含量限制值。根据IEC闪变仪的构成原理和光闪变发生机理，可以认为：不论输入 IEC闪变仪电压形式及灯参数如何，同样频率与波动幅度的光通量波动，可以产生相同的闪变效果[11,24]。因此，当输入 IEC闪变仪模块 3-22相同波动频率与波动幅度的光通量波动信号 dLum(t)时，将得到相同的闪变评价值 Pst。于是，可分解出用于实验研究的IEC闪变仪分解模型，如图3所示。

图3 闪变仪的分解模型Fig.3 Improved flickermeter model

针对实验直接获得的光通量信号Φ(t)，将对于光通量信号Φ(t)处理后得到的光通量波动信号 dLum(t)直接导入到模块 3-22，从而得出 Pst。该模型略去了IEC原模型中产生电压波动的带通滤波器和产生光通量波动的灯环节，可以很方便地用于实验研究。

2.3 对分解模型的验证

首先，对IEC闪变仪的仿真程序输入不同频率与含量的间谐波电压，可得到这个电压条件下的光闪变强度Pst，中间参量 dLum(t)、eye(t)的波动曲线。间谐波的电压形式为

式中，V为基波电压的有效值，f0为基波电压频率，f为间谐波电压频率，m为间谐波电压的含量。

对于 230V/50Hz的白炽灯，当输入频率 f= 40Hz，间谐波含量m=1%的间谐波时，得到Pst= 3.8092，并得出中间参量的波动曲线如图 4、图 5所示，即为光通量波动曲线 dLum(t)，其波动幅度ΔLum=0.094；视觉反应信号曲线 eye(t)，其波动幅度Δeye=0.038，且这两条曲线的波动频率均为10Hz。

图4 dLum(t)曲线Fig.4 Curve of dLum(t)

图5 eye(t)曲线Fig.5 Curve of eye(t)

现在，在实验条件下用分解模型计算其短时闪变强度 Pst。实验中，使用照度计接收光源的瞬时照度曲线，由于照度与光源的光通量呈线性关系，因此照度曲线即可代表光通量信号。将光通量信号Φ(t)进行标幺化，并提取其包络线波动作为光通量波动曲线dLum(t)，将这个曲线导入到分解模型中，来计算其闪变强度Pst。

对于 230V/50Hz的白炽灯，当输入 f=40Hz， m=1%的间谐波电压时，获取实验得到的光通量信号Φ(t)，导入分解模型中进行计算，得到 Pst=2.1369，并得出中间参量 dLum(t)、eye(t)的波动曲线：光通量波动信号的波动幅度ΔLum=0.053，视觉曲线的波动幅度Δeye=0.022，这两个曲线的波动频率均为10Hz。再对f=40Hz，m=2%与f=42Hz，m=1%两种间谐波电压条件下进行实验。用IEC闪变仪程序仿真计算的结果，与对实验获得的光通量数据用分解模型程序进行计算的结果进行对比，中间参量波动幅值ΔLum、Δeye和 Pst如表 1所示。

表1 仿真与实验条件下计算值对比Tab.1 Comparison of calculation between simulation and experimental results

由表1可知，在不同的电压条件下，无论是IEC仿真程序计算还是用分解模型对实验数据进行计算，得到ΔLum/Δeye、ΔLum/Pst的值的变化量都很小，可以认为是一个恒定值，且在不同的电压条件下，无论是仿真计算还是对实验数据计算，ΔLum、Δeye和Pst三者之间存在一定的线性关系；在相同电压条件下，从表中可知：仿真计算下的ΔLum/Δeye、ΔLum/Pst与实验条件计算下的结果很接近。因此可以认为不论是仿真计算还是对实验数据的计算，ΔLum、Δeye与Pst之间的线性关系都是相同的。由此可知，只要在模块3-22中输入一定波动频率与波动幅度的光通量波动dLum(t)曲线时，便会得到相同波动频率与一定波动幅度的eye(t)曲线，并得到相应的Pst值。

之所以在同样电压条件下，仿真计算与对实验数据的计算得到的ΔLum、Δeye和 Pst不同，是因为在使用分解模型时，导入了光源直接产生的光通量波动曲线，需要在模块 3-22之前的环节乘以一个修正系数k。设修正后光通量波动为dLum(t)_new，则可以得到二者关系式为dLum(t)_new=k·dLum(t)。调整k=1.85后，再进行计算，可得 Pst=3.953 3，与仿真计算得到的结果Pst=3.809 2非常接近。

在分解模型中乘以修正系数 k=1.85进行修正后，重新计算。在 f=40Hz，m=1%的间谐波的实验条件下，对获得的光通量曲线Φ(t)进行计算处理，得到中间过程 dLum(t)、eye(t)如图 6、图 7所示，ΔLum约为 0.088，Δeye约为0.038，Pst为 3.94，对比可知，与仿真结果非常接近。

图6 dLum(t)曲线Fig.6 Curve of dLum(t)

图7 eye(t)曲线Fig.7 Curve of eye(t)

修正后不同实验条件下的计算结果与仿真计算的对比如表 2所示。表中 Pst1为仿真计算得到的光闪变强度，Pst2为修正分解模型后，对实验结果进行计算得到的光闪变强度。

表2 仿真与实验条件下Pst计算的对比Tab.2 Calculation of Pstcomparison between simulation and experimental results

由表 1中(Pst2-Pst1)/Pst1的计算结果可知，Pst2与Pst1非常接近，因此用本文提出的闪变仪的分解模型进行计算得到的Pst是准确的。

对于荧光灯及其他类型的灯这个验证结果也同样成立，因为本文提出的改进模型是直接输入光通量波动曲线得到的计算结果，与前面的灯环节没有关系。

上述分解模型主要用于通过实验方法对闪变效应的研究和评价，由于人眼对光闪变的敏感性与光波动频率及幅度密切相关，对8.8Hz左右频率光通量波动尤为敏感。这就对使用该模型时的实验数据获取提出了较高要求，特别是光通量数据采集仪器的敏感性和精确度，本文所使用的 T-10照度计，最高准确度可以达到 1 lx。实际中，当光通量太小时，波动测量的准确性降低，不能作为评价依据；另一方面使用该分解模型是建立在相同光通量波动产生相同闪变效应的基础上，这在波动波形基本呈正弦的情况下是成立的，但如果波形畸变严重时，上述基础是否仍然成立尚待研究。

3 实验装置

整个实验系统的目的是获取不同的荧光灯在不同的间谐波电压条件下的光通量信号曲线Φ(t)，以计算其光闪变强度 Pst。整个实验装置系统可以分为四个部分：

（1）间谐波电压输出（generating interharmonic voltage fluctuation）：用来输出含间谐波含量的正弦电压给灯具，使灯具发光。

（2）照明箱（lighting booth）：给灯具提供封闭的照明环境，以隔绝外来杂散光的影响，并放置照度计在其中读取光通量信号。

（3）光通量数据获取（luminance data acquisition system）：使用柯尼卡公司的T-10高准确度照度计来采集光通量信号数据，然后将数据送入示波器中，使用示波器获取光通量信号Φ(t)。

（4）Pst计算（quantifying the flickering severity）：对于读取的光通量信号Φ(t)，通过分解模型的计算程序来计算其 Pst。

图8所示为整个实验系统的实物连接图以及原理框图。

3.1 间谐波电压输出

图8 实验装置连接原理框图Fig.8 Block diagram of experimental installation connecting

使用Chroma（致茂）公司的设备Chroma 61505来发生间谐波电压，并输出给灯具。Chroma是一台可程控交流电压供应器，可以输出包含谐波、间谐波在内的不同类型的电压。通过数据接口 RS 232可将Chroma与计算机连接起来，并使用配套的软件平台Chroma 615_616 soft panel来控制设备。

在软件soft panel的主界面，设置输出电压的基波频率为 50Hz，有效值为 220V。然后在soft panel的interharmonic选项卡中，设置输出间谐波的频率、含量与时长，便可输出叠加在基波上的间谐波电压。间谐波频率范围可在0.01～2 400Hz（精确到0.01Hz）内变化，间谐波含量值是以基波幅值为基础的百分比含量，其准确度为0.1%。如可设置频率为40Hz、含量为1.2%的间谐波。将Chroma产生的电压通过输出线输出，即可将电压供给光源。

3.2 照明实验箱

照明实验箱为一个35cm×33cm×37.5cm的纸质箱体，内部有两个部分：照明输出与光通量接收。

将灯具安装在箱壁上，并将 Chroma输出的电压输入给灯具。控制 Chroma电压输出时可以控制灯具的照明情况。将实验箱体封闭，可避免外来杂散光的干扰，这样箱内接收光照的照度计可以正确反映光源发出的光通量的情况。实验中使用的灯具为 1支白炽灯与3支荧光灯，型号分别为：白炽灯：欧普 OPEL PZ220-60W（标准为 GB/T10681-2009）；紧凑型荧光灯：飞利浦 YPZ220/8-2U.RR.D，飞利浦YPZ220/14-2U.RR.D，荧火虫YPZ220/8-2U.RR.D。

实验中使用照度计采集光源投射在箱体内壁的光照度。照度计采集的是照度计安装面的照度值，由于照度计安置在相对灯源固定的位置，而照度与光源的光通量是成正比关系。因此，照度的波动情况就反映了光通量的波动情况。

实验中选用柯尼卡公司的 T-10照度计，照度计通过外部的光接收积分球来接收光源的光信号，其相对光谱感应与国际照明委员会CIE光谱视觉效率V(λ)的8%(f1)相匹配。光信号经过光电二极管后转化为电流信号，再经过放大电路，放大为电压信号输出。照度计模拟输出的准确度为1mV/位，90%响应时间为 1ms。光接收积分球接收到的瞬时光通量信号与模拟输出的电压信号成正比关系。调节照度计的量程档，当光通量达到满量程 3 000lx时，输出电压为照度计的最大饱和电压3V。

3.3 光通量数据获取

实验中使用泰克公司的Tektronix MSO 5104示波器。示波器的模拟带宽为1GHz，最高10G/s的采样率，DC增益准确度为±1.5%。将照度计输出电压信号输入给示波器，即可在示波器上显示电压信号波动，并可将这个电压波动的数字信号保存下来。设置示波器的采样率为100k/s，读取1s的波动信号。可以观察到1s内的光通量曲线有100个波动，可知其波动频率为基波频率的 2倍。

3.4 Pst计算

实验中，将照度计获取到的光通量曲线提取出其标幺化的光通量波动包络曲线，然后输入分解模型中，即可得Pst。取光通量曲线Φ(t)中影响人眼光反应效果的上包络线作为光通量波动曲线dLum(t)。闪变仪分解模型程序的计算步骤如图9所示。

图9 Pst的计算流程Fig.9 The calculation process of Pst

在取定的间谐波频率下，Pst会随着间谐波含量m的变化而变化。调节 m，使 Pst＝1，此时的间谐波含量m即为间谐波含量限制值m0。由于电压发生设备Chroma的设置中，间谐波含量m的准确度为0.1%，因此可以认为，当计算得到Pst值在0.9～1.1时，Pst＝1。

在实验过程中，有几点需要注意：

（1）由于荧光灯发光特性，在刚刚点燃时其光通量处于不断升高的阶段。荧光灯需要点燃后经过一段时间，其光通量才能稳定下来。因此，输入间谐波电压给荧光灯后，应等待约 3min后，才能开始用照度计获取其光通量数据。

（2）在照明箱中，灯不宜离照度计太近，以免照度计的照度超出量程，输出电压超出最大饱和电压。应当保持输出的电压与灯的光通量的关系处于线性区域。

（3）实验时，应当将盖上照明箱盖子进行封闭，以避免外界光源的干扰。

（4）可以在照明箱上开通一个小孔，在实验时通过小孔肉眼观察灯的闪变情况，验证此时是否可以观察到光闪变。

4 实验结果

4.1 光闪变限制曲线的获得

对于一特定光源，改变间谐波电压的频率 f与含量m，使该电压条件下Pst＝1，则此时的m即为该频率f下的间谐波含量限制值m0，通过该方法得到的点（f，m0）构成的曲线，即为该光源的光闪变限制曲线。由于不同光源的电路构成不同，其在相同的电压条件下的闪变效果也不同。其光闪变限制曲线也不同。

已有研究成果显示，电压中的间谐波分量导致的电压闪变频率 f△与间谐波频率 f有如下关系[4-6]式中，f0为基波频率；H为间谐波最接近的谐波频率的次数；f△＜50Hz。不同的间谐波频率可能会导致相同的电压闪变频率，如58Hz和158Hz的间谐波都导致8Hz的电压波动。文献[6]还指出：具有相同 f△的不同频率间谐波，若其幅值相同，则其导致的电压波动峰值相同，但波动有效值不同[6]。

以飞利浦14W 荧光灯为研究对象。取H＝1，间谐波频率 f=40Hz时，改变间谐波含量 m的取值，对光通量曲线进行 Pst计算，得到的结果如表3所示。

表3 14W飞利浦CFL灯在40Hz间谐波下的Pst值Tab.3 Pstof 14W Philips CFL under 40Hz interharmonic

由上表可知，当 m=1.2%时，Pst值最接近 1。因此可以认为该灯在 f=40Hz下的间谐波含量临界值m0=1.2%。用同样的办法，可以求得14W 飞利浦CFL灯在 H＝1时，频率从 25～75Hz变化下间谐波含量限制值 m0的取值如表4所示。

表4 14W飞利浦CFL灯间谐波含量限制值Tab.4 Interharmonic limit of 14W Philips CFL

根据上表的实验结果，可以作出14W 飞利浦灯在Pst=1时的光闪变限制曲线，如图 10所示，从中看出间谐波含量限制值m0随频率的变化情况。

图10 14W飞利浦灯的闪变限制曲线Fig.10 Flicker limit curve of 14W Philips CFL

由图10可知：14W 飞利浦CFL与白炽灯的间谐波闪变限制曲线的走向趋势相似，都是由以f=50Hz为对称轴的两支接近对称的 V字型曲线分支构成。当 f=41Hz与f=59Hz时，光通量波动频率为 9Hz，间谐波限制含量达到最小值，光源在这个频率下最易发生闪变；而当间谐波频率越远离f=41Hz与f=59Hz时，间谐波含量限制值变大。这个规律与视感度系数曲线中的规律一致，当 f=8.8Hz（接近9Hz）时瞬时闪变视感度达到最大值，此时人眼对灯光闪烁最为敏感。这表明实验所得的间谐波闪变限制曲线是正确的。

在H=3、H=5时，使f△从2～25Hz变化，用同样的方法进行实验，获取高频间谐波下 14W 飞利浦荧光灯在不同频率下的间谐波含量限制值如表5、表6所示。

表5 14W飞利浦CFL灯H=3时间谐波含量限制值Tab.5 Interharmonic limit of 14W Philips CFL when H=3

表6 14W飞利浦CFL灯H=5时间谐波含量限制值Tab.6 Interharmonic limit of 14W Philips CFL when H=5

从而可获得14W飞利浦灯在H=1，H=3，H=5时不同频率下的闪变限制曲线，如图11所示。

图11 14W飞利浦灯的闪变限制曲线Fig.11 Flicker limit curve of 14W Philips CFL

由图11中可知：在高频间谐波下（H=3，H=5时）紧凑型荧光灯的光闪变限制曲线的走向规律与低频时一致，另外，在相同的间谐波电压波动频率f△下，高频下的间谐波限制含量比低频时更大，紧凑型荧光灯对低频间谐波电压更为敏感。

4.2 不同光源的间谐波光闪变限制曲线及其对比

采用同样的方法，对不同功率和品牌的紧凑型荧光灯进行实验研究，可以得到相似的结果。表 7～表9所示为8W飞利浦灯H＝1、H=3、H=5时，间谐波限制值 m0的取值；表 10为荧火虫灯 H=1时间谐波限制值m0的取值。图12为14W飞利浦灯、8W飞利浦灯、8W荧火虫灯在H＝1时（低频间谐波下）的间谐波光闪变限制曲线。图13为8W飞利浦灯在H＝1、H=3、H=5时的间谐波光闪变限制曲线的对比。

表7 8W飞利浦CFL当H=1时间谐波含量限制值Tab.7 Interharmonic limit of 8W Philips CFL when H=1

表8 8W飞利浦CFL灯H=3时间谐波含量限制值Tab.8 Interharmonic limit of 8W Philips CFL when H=3

表9 8W飞利浦CFL灯H=5时间谐波含量限制值Tab.9 Interharmonic limit of 8W Philips CFL when H=5

表10 8W荧火虫CFL灯H=1时间谐波含量限制值Tab.10 Interharmonic limit of 8W Yihuochong CFL when H=1

图12 14W飞利浦灯、8W飞利浦灯、8W荧火虫灯的闪变限制曲线Fig.12 Flicker limit curve of 14W Philips CFL、8W Philips CFL and 8W Yinghuochong CFL

将间谐波导致的电压波动规律与图 13所示的光闪变实验结果进行对比，可以看出，能引起相同电压闪变频率和峰值波动深度的间谐波，会引起不同的光源光闪变效应，说明间谐波引起的电压有效值波动是决定光闪变的重要因素。图13的结果还表明，光源的光闪变仅对奇数次谐波附近的间谐波敏感，对偶数次谐波附近的间谐波则几乎没有限制要求。

图13 8W飞利浦灯在H=1，3，5下的闪变限制曲线Fig.13 Flicker limit curve of 8W Philips CFL when H=1，3，5

由上述实验结果可以得到如下结论：不同品牌和功率的光源，其闪变限制曲线有所不同。总的来说，高频和低频间谐波都可能引发紧凑型荧光灯闪变，但低频间谐波比高频间谐波更敏感，这一结论及相应的间谐波闪变曲线是使用IEC闪变仪无法获得的；光源功率越小，对间谐波越敏感，即间谐波限制值越低；而不同品牌、相同功率光源，对间谐波限制值差异不大。

5 结论

通过分析和实验，获得了基于IEC闪变仪的分解模型，该模型可以有效地用于针对各种光源的间谐波光闪变效应实验研究；建立了紧凑型荧光灯在间谐波条件下闪变效应的实验研究装置和方法，利用该装置和方法可以获得不同光源对不同频率间谐波引发闪变效应的幅值限制值，该限制值利用 IEC闪变仪无法得到；对不同品牌和功率的紧凑型荧光灯的实验研究结果表明：高频和低频间谐波都可能引发紧凑型荧光灯闪变，但低频间谐波比高频间谐波更敏感；同时光源功率对间谐波闪变限制值有一定影响。

[1] Yong J, Sun C, Xu W. Voltage flicker caused by two interharmonics[C]. Canadian Conference on Electrical and Computer Engineering, 2006: 239-242.

[2] Yong J, Thavatchai T, Xu W. Characterizing voltage fluctuations caused by a pair of interharmonics[J]. IEEE Trans. on Power Delivery, 2008, 23(1): 319-327.

[3] Li C, Xu W, Tayjasanant T. Interharmonics: basic concepts and techniques for their detection and measurement[J]. Electric Power Systems Research, 2003, 66(1): 39-48.

[4] Yacamini R. Power system harmonics-part 4 interharmonics[J]. Power Engineering Journal, 1996, 10(4): 185-193.

[5] Mombauer W. Flicker caused by interharmonics[J]. EtzArchiv, 1990, 2(12): 391-396.

[6] Tayjasanant T, Wang W, Li C, et al. Interharmonicflicker curves[J]. IEEE Trans. on Power Delivery, 2005, 20(2): 1017-1024.

[7] Morcos M, Gomez J. Flicker sources and mitigation [J]. IEEE Power Engineering Review, 2002, 22(11): 5-10.

[8] 李霏霏, 杨洪耕, 惠锦, 等. 一种由间谐波估计电压闪变参数的简便方法[J]. 电力系统保护与控制, 2011: 39(22): 83-89.

Li Feifei, Yang Honggen, Hui Jin, et al. A simplemethod of voltage flicker estimation based on interharmonics[J]. Power System Protection and Control, 2011, 39(22): 83-89.

[9] 王建勋, 刘会金. 间谐波闪变效应计算及闪变源识别方法[J]. 电力系统自动化, 2011, 35(11): 52-58.

Wang Jianxun, Liu Huijin. A calculation method for interharmonics-caused flicker and flicker source identification[J]. Automation of Electric Power Systems, 2011, 35(11): 52-58.

[10] 孙成发, 高辉. 一种提高短时闪变严重度Pst计算准确度的方法[J]. 电力系统保护与控制, 2008, 36(16): 48-56.

Sun Chengfa, Gao Hui. A method to improve calculating accuracy of the short term flicker severity Pst[J]. Power System Protection and Control, 2008, 36(16): 48-56.

[11] IEC 61000-4-15 Testing and measurement techniques: flickermeter-functional and design specifications[S]. Geneva. Switzerland: IEC, 2003.

[12] 雍静, 孙才新. 间谐波源模型和间谐波电压特性及其闪变效应的研究[D]. 重庆: 重庆大学, 2007.

[13] 雍静, 孙才新, 曾礼强, 等. 基于热平衡方程的改进的白炽灯闪变仪模型[J]. 电工技术学报, 2008, 23(9): 118-124.

Yong Jing, Sun Caixin, Zeng Liqiang, et al. An improved flickermeter model for incandescent lamp based on heat balance equation[J]. Transactions of China Electrotechnical Society, 2008, 23(9): 118-124.

[14] Masi M, Peretto L, Tinarelli R, et al. Assessment of human annoyance under flicker condition[C]. IEEE International Instrumentation and Measurement Technology Conference, Binjiang, 2011.

[15] Emanuel A, Peretto L. The response of fluorescent lamp with magnetic ballast to voltage distortion[J]. IEEE Trans. on Power Delivery, 1997, 12(1): 289-295.

[16] Gluskin E, Frangiskos V, Kateri I, et al. The instantaneous light-intensity function of a fluorescent lamp[J]. Physics Letters A, 2006, 353: 355-363.

[17] Chen S, Lo C, Foo M, et al. Testing of fluorescent lamps for its flickering susceptibility towards interharmonic voltages[C]. IEEE Power Engineering Conference, Singapore, 2007.

[18] Koster M, Jaeger E, Vancoetsem W. Light flicker caused by interharmonics[R/OL]. [2001]. http://grouper. Ieee.org/groups/harmonic/iharm/docs/ihflicker.pdf.

[19] 张娜, 雍静, 曾礼强. 关于 IEC闪变仪无法检测由高频间谐波引起闪变的情况分析[J]. 低压电器, 2009(6): 5-7.

Zhang Na, Yong Jing, Zeng Liqiang. Analysis about the condition of IEC flickermeter’s unable to dectect flicker caused by high frequency interharmonic[J]. Low Voltage Apparatus, 2009(6): 5-7.

[20] 马玉强, 张有玉, 武剑. IEC闪变仪对间谐波引起的电压闪变测量误差的分析[J]. 电力系统保护与控制, 2010, 38(1): 23-27.

Ma Yuqiang, Zhang Youyu, Wu Jian. Analysis of the IEC flickermeter measurement error for measureing interharmonic-caused voltage flickers[J]. Power System Protection and Control, 2010, 38(1): 23-27.

[21] 贾秀芳, 赵成勇, 胥国毅, 等. IEC闪变仪误差分析及改进设计[J]. 电工技术学报, 2006, 21(11): 121-126.

Jia Xiufang, Zhao Chengyong, Xu Guoyi, et al. Error analyzing of IEC flickermeter and its improving design [J]. Transactions of China Electrotechnical Society, 2006, 21(11): 121-126.

[22] 雍静, 李建波, 王晓静, 等. 含间谐波电压下荧光灯的功率响应[J]. 重庆大学学报, 2008, 31(3): 263-266.

Yong Jing, Li Jianbo, Wang Xiaojing, et al. Power response of fluorescent lamp with voltage containing interharmonic[J]. Journal of Chongqing University, 2008, 31(3): 263-266.

[23] Wang C, Devaney M, Yang S. Decomposition of the IEC flickermeter weighting curves[C]. Instrumentation and Measurement Technology Conference, Italy, 2004.

[24] Drá pela J, Toman P. Interharmonic-flicker curves of lamps and compatibility lever for interharmonic voltages [J]. IEEE Lausanne Power Tech., 2007: 1552-1557.

Experimental Study for Flicker of Compact Fluorescent Lamp Caused by Interharmonics

Yong Jing Yan Xiaolong Zeng Liqiang

（State Key Laboratory of Power Transmission Equipment & System Security and New Technology Chongqing University Chongqing 400030 China）

In order to conduct experimental study for flicker, a decomposed flickermeter model is developed by decomposing the weighting filter of IEC flickermeter. Luminous flux signal acquired from experiments can be input directly into this model to calculate the short-term severity value Pst, which is the index to assess the flicker severity. The feasibility and effectiveness of this model is experimentally verified. The design and establishment process of experimental facility is also presented in the paper. The high-precision illuminance meter is applied to acquire luminous flux signal of the compact fluorescent lamp(CFL) supplied by voltage containing interharmonics with given frequency and magnitude. Experimental studies for CFL light flicker under voltages containing interharmonics with various magnitudes and frequencies are conducted by using the proposed decomposed model. The short-term severity value Pstare obtained, and therefore the interharmonic limit curves for light flicker of compact fluorescent lamp are proposed.

Interharmonic, flickermeter, luminous flux, flicker, interharmonic limit curve

TM727

雍 静 女，1964年生，博士，教授，主要研究方向为电能质量。晏小龙 男，1988年生，硕士研究生，主要研究方向为电能质量。

国家自然科学基金资助项目（51207174）。

2013-02-27 改稿日期 2013-04-17