基于人工神经网络的缝翼凹槽填充降噪设计
2015-04-10徐康乐
陶 俊,孙 刚,*,徐康乐
(1.复旦大学力学与工程科学系,上海 200433;2.中国商飞上海飞机设计研究院,上海 201210)
基于人工神经网络的缝翼凹槽填充降噪设计
陶 俊1,孙 刚1,*,徐康乐2
(1.复旦大学力学与工程科学系,上海 200433;2.中国商飞上海飞机设计研究院,上海 201210)
缝翼凹槽填充技术作为一种缝翼降噪方法,有可能会造成气动性能的损失,如最大升力系数和失速迎角的减小。基于这种情况,针对某多段翼型建立了缝翼凹槽填充构型的数据库,挑选出参考构型,利用置信度推理确定了优化方向,生成了20个优化构型;采用back propagation(BP)人工神经网络快速预测各优化构型的气动性能,选择其中气动性能最好的构型作为设计构型进行校核计算,求解定常Navier-Stokes方程评估其气动性能与基准构型作对比,应用CFD和声类比相结合的混合方法评估其气动噪声性能并与基准构型作对比。结果表明:在保持多段翼型气动性能的同时,对于给定观测点,所设计的缝翼凹槽填充构型使得气动噪声明显降低。
缝翼凹槽填充;多段翼型;人工神经网络;气动噪声;混合方法
0 引言
自从20世纪70年代初,联邦航空条例FAR-36和国际民航公约第十六号附件颁布以来,噪声就成为了民用飞机适航取证必须遵守的强制性指标。FAR-36第四阶段[1]要求2006年之后申请适航的新型民用飞机比第三阶段降低10EPNdB。NASA计划,较1997年的水平,在25年内将噪声降低20 dB[2];而欧盟(EU)在其民航2020远景规划[3]中提出,较2000年的水平,噪声将降低10 dB。由此可见,噪声性能是关系到民用飞机能否立足于市场的关键问题。
近几十年来,随着高涵道比涡扇发动机的应用,航空发动机噪声大幅度降低,机体噪声成为飞机起降时的主要噪声源[4-5],尤其当飞机降落时,机体噪声已与发动机噪声相当[6]。
实验研究表明[7-9],增升装置气动噪声是机体噪声的主要噪声源,尤其当飞机起飞着陆时,在飞机机体辐射噪声中,增升装置气动噪声占有相当大的比重。降低增升装置的气动噪声对于降低飞机的总体噪声有着至关重要的意义,同时也是目前飞机设计者必须面对的一个难题。缝翼凹槽填充[10](slat cove filler,简称SCF)是一种比较常见的降噪措施,SCF的设计旨在形成一个大幅度连续的外形以取代传统缝翼尖端不连续的外形,从而抑制缝翼尖端剪切层的形成,同时消除缝翼凹槽内的涡,因此达到降低宽频噪声的目的。NASA和Boeing公司为考察SCF的降噪效果,开展了一些实验研究,W.Clifton Horne等人对Boeing777的26%缩比模型加装SCF,在NASA Ames的40 ft×80 ft风洞中进行了气动噪声实验,测量了SCF对气动噪声的影响[11];Craig L.Streett等人对Trap wing高升力模型加装SCF,在NASA Langley的14 ft×22 ft亚音速风洞中进行了气动噪声实验,考察了SCF的降噪效果[13]。这些实验表明SCF能够有效地降低气动噪声,然而,有研究指出[12-13],在噪声降低的同时,气动性能如最大升力系数、失速迎角等可能也会随之损失。
为保持SCF构型的气动性能,国外学者进行了一些设计研究,日本宇宙航空研究开发机构(JAXA)的Taro Imamura等人基于两个迎角下的流线外形,设计了两个SCF构型,进行风洞实验,从中挑选出了气动性能接近基准构型的一个作为最终构型[14],Boeing公司的Arvin Shmilovich等人针对EET多段翼型,基于多种流线外形设计了若干SCF构型,并利用O-verflow程序考察了这些SCF构型的气动性能[15]。但这些研究多是一些尝试性设计,尚未形成系统的设计方法。
鉴于此,本文选取某多段翼型,建立了一个SCF构型的数据库;通过置信度分析,确定了优化设计方向,并以此方向从数据库中挑选出参考构型生成了20个优化构型;以数据库中的构型训练了back propagation(BP)人工神经网络,并以训练好的BP人工神经网络预测了20个优化构型的气动性能;从中挑选气动性能最好的作为设计构型进行了校核计算,求解Navier-Stokes(N-S)方程评估其气动性能,采用CFD与声类比相结合的混合方法评估其气动噪声性能。此外,为验证计算方法的可靠性,对圆柱绕流气动噪声进行了验证计算,并与实验结果进行了对比。
1 控制方程和数值计算方法
本文求解定常N-S方程以评估多段翼型的气动性能;应用CFD与声类比相结合的混合方法评估其气动噪声性能,其中CFD部分求解非定常N-S方程获得近场的脉动压力信息,声类比部分以近场脉动压力信息作为声源项求解 Ffowcs Williams-Hawkings (FW-H)方程获得远场气动噪声。
1.1 流场控制方程及其求解
守恒形式的三维可压缩N-S方程可写为:

其中Q、F、G和H的定义见文献[16]。
选用S-A湍流模型,空间离散采用Roe-FDS方法,时间离散采用隐式LU-SGS方法,非定常求解采用双时间方法。
1.2 FW-H方程及其求解
FW-H方程[17]是将N-S方程按非齐次波动方程形式重新整理而成,能精确地描述在静止流体中作任意运动的物体与流体相互作用的发声问题,是气动声学的理论基础之一。FW-H方程的微分形式可写为:
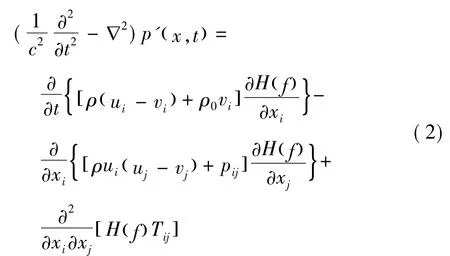
方程(2)右端三项分别代表厚度噪声、载荷噪声和四极子噪声。其中 ()为波动算子; p'(x,t)表示观测点在t时刻的声压值;c,ρ,ui,pij分别表示声速、密度、速度和应力张量;Tij=ρuiuj-σij+ ( p-c2ρ')δij为Lighthill应力张量;δij为Kronecker符号;下标“0”表示未扰动量;撇号表示扰动量;H(f)为Heaviside函数,满足:

其中函数f(x,t)表示积分面,并满足:在积分面外,f(x,t)>0;在积分面上,f(x,t)=0;在积分面内,f(x,t)<0。若取积分面为物面,则可得到不可穿透积分面FW-H方程。
20世纪70年代末到80年代初,Farassat从不可穿透积分面FW-H方程出发,推导出了FW-H方程中厚度噪声和载荷噪声解的时域表达式,即著名的Farassat 1和 Farassat 1A公式[18]。由于 Farassat 1A公式比Farassat 1公式更易于进行数值计算,这里采用Farassat 1A公式,其表达式如下:

其中字母上方的圆点表示时间导数;下标“ret”表示延迟时刻的值;下标“T”和“L”分别表示厚度噪声与载荷噪声;ri为由声源指向观测点的矢径;Mi定义为Mi=vi/c,并且:
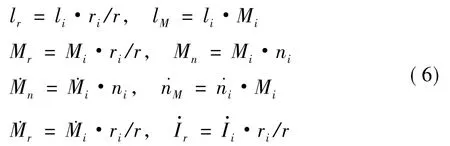
Farassat 1A公式可求解厚度噪声和载荷噪声,但对四极子噪声无能为力,为了计算四极子噪声,di Francescantonio从式(2)形式的FW-H方程出发,借用Kirchhoff方法的思想,提出了 K-FWH方法[19]。K-FWH方法选取包含物面的可穿透运动面进行积分,其控制方程为:


因为方程(7)在形式上和不可穿透积分面FW-H方程完全一致,所以也可采用Farassat 1A公式求解。K-FWH方法的特点在于:包含物面的可穿透运动面的面积分中体现了非线性区域四极子噪声的贡献,因此根据Farassat 1A公式求解所得的厚度噪声和载荷噪声之和即为总的气动噪声。
由于Farassat 1A公式是时域方法,为获得气动噪声的频谱信息,本文对时域解采用了快速傅里叶变换(FFT)。
2 计算方法验证
为验证所建立的气动噪声计算方法,本文基于文献[20]中的圆柱绕流实验,进行了圆柱绕流气动噪声的算例验证。圆柱直径D=0.019 m,计算条件为:自由来流马赫数Ma=0.2,基于圆柱直径的雷诺数Re=90 000。数值计算的网格单元数为33万,非定常计算的时间步长Δt=5×10-5s。
图1为t=0.02 s时刻的涡强分布图。从图中可以看到圆柱后缘大尺度的、交替性的涡脱落。

图1 圆柱绕流的涡强分布Fig.1 Vorticity magnitude distribution of the cylinder
根据实验,在距离圆柱中心点下游128D处设置观测点,计算观测点处的气动噪声。图2给出了本文数值模拟获得的观测点处声压随时间的变化,可以看出,随着时间的推移,声压作周期性的变化。图3给出了观测点处计算所得声压级(Sound Pressure Level,简称SPL)频谱与实验结果的对比。从对比结果来看,计算所得频谱与实验频谱吻合较好,频谱峰值比较接近,都为98 dB左右,并且峰值位置几乎一致,都在650 Hz左右。由对比结果可见,本文所建立的气动噪声计算方法是可靠的。

图2 观测点处声压随时间的变化Fig.2 Variation of acoustic pressure with time at the observation point

图3 观测点处声压级频谱计算结果与实验结果对比Fig.3 SPL spectrum comparison of computational results with experiment results at the observation point
3 SCF设计
SCF属于缝翼降噪技术,为考察缝翼降噪效果,本文选取如图4所示的包含缝翼和主翼的二段翼型作为设计对象。

图4 计算所用二段翼模型Fig.4 Dual-element airfoil model for computation
典型的SCF外形如图5中红线所示,图中各点坐标已沿y方向归一化,各点之间通过引入累加弦长作为参数构造的三次样条参数曲线[21]联接,从而生成SCF外形,其中x0和x5已知,x1、x2、x3、x4即为设计变量。

图5 典型的SCF外形Fig.5 A typical SCF shape
图6给出了求解定常N-S方程所得基准构型的升力曲线,计算网格数为35万,计算条件为:自由来流马赫数Ma=0.2,基于翼型弦长的雷诺数Re=4.6 ×106。从图6中可见,基准构型的失速迎角在32°左右,最大升力系数为2.906。为保证设计构型的气动性能,本文SCF的设计目标即为使得设计构型在32°迎角下,Ma=0.2,Re=4.6×106时的升力系数(以下简称设计点升力系数)接近或大于基准构型的最大升力系数。

图6 基准构型升力曲线Fig.6 Lift curve of the baseline configuration
具体设计步骤如下:1)建立SCF的数据库,对于每个SCF构型都包含几何参数和气动参数;2)挑选出气动性能最接近基准构型的构型作为参考构型,进行置信度分析,确定优化方向;3)按照步骤2确定的优化方向生成若干优化构型,并以数据库中的SCF构型作为样本,训练BP人工神经网络;4)利用训练好的BP网络快速预测各优化构型的气动性能;5)挑选出气动性能最好的优化构型作为设计构型,进行校核计算。
大部分心外膜起源室早的心电图表现与对应的心内膜起源室早相似,但其QRS波起始部上升较缓,可见假delta波。 Doppalapudi等[6]报道,从QRS波起始部到顶峰所需时间长于整个QRS波时限的一半以上(>0.55)。这类室早的常见起源部位在冠状窦分支附近,如心大静脉和前室间静脉等。
本文建立的SCF数据库包含24个构型,如表1

表1 SCF构型数据库Table 1 Database of SCF configurations
所示,其中几何参数即x1、x2、x3、x4,气动参数Cl即设计点升力系数。
为确定优化方向,这里采用置信度推理方法,引入统计学中正相关函数作为推理的置信度,对于一个两变量问题,相关系数表达式为:
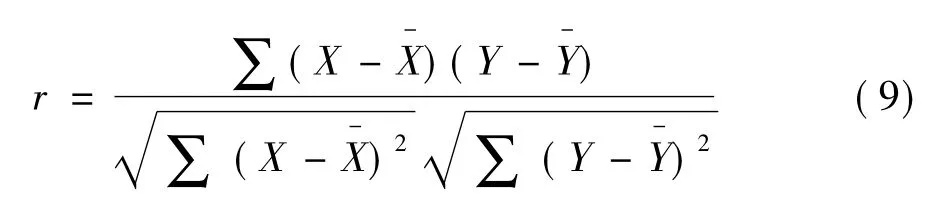
|r|=1表明变量X与Y完全线性相关,|r|=0则表示不存在线性相关。一般认为|r|>0.7时推理是可信的,于是强化联结;当|r|<0.3则弱化甚至切断相关联结。表2给出了设计点升力系数与几何参数x1、x2、x3、x4之间的相关系数。

表2 设计点升力系数与几何参数之间的相关系数Table 2 Related coefficients between lift coefficient on the design conditions and geometry parameters
从相关系数可以看出,设计点升力系数与x1、x2、x3、x4都呈负相关,即可以认为设计点升力系数很大程度上随着x1、x2、x3、x4的减小而增大。由表1可知数据库中第15号构型的设计点升力系数为2.825,与基准构型的最大升力系数最接近,因此挑选第15号构型为参考构型,按照优化方向即减小x1、x2、x3、x4,生成了20个优化构型,如表3所示。
为了能够快速考察优化构型的气动性能,建立了如图7所示的BP人工神经网络进行预测,其中输入神经元四个即x1、x2、x3、x4,隐层神经元四个,输出神经元一个即设计点升力系数。
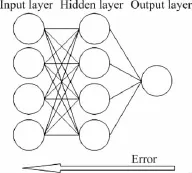
图7 BP人工神经网络的结构Fig.7 Structure of the BP artificial neural network
为训练该BP神经网络,选取表1中的数据库作为训练样本,表4给出了训练样本升力系数神经网络预测结果和N-S方程计算结果的比较,其中N-S方程计算的网格数均为35万左右。从表4可以看出,对于训练样本,最大误差仅有0.24%,可见训练效果相当好。针对表4中的优化构型,用已训练好的BP网络进行预测,其结果如表5所示。从表5可以看出,优化构型12的设计点升力系数为2.917,是所有优化构型中最高的,并且高于基准构型的最大升力系数2.906。因此,本文选取优化构型12作为设计构型进行校核计算。

表3 20个SCF优化构型的几何参数Table 3 Geometry parameters the 20 optimized SCF configurations

表4 神经网络预测和N-S方程计算的升力系数对比Table 4 Lift coefficient comparisons of neural network prediction results with N-S equation simulation results
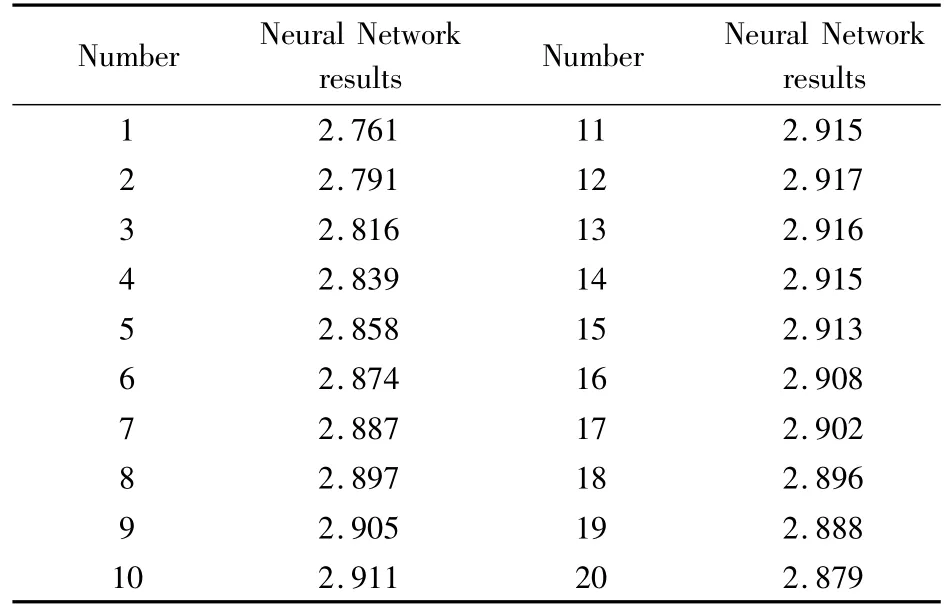
表5 优化构型神经网络预测结果Table 5 Neural network prediction results of the optimized configurations
4 校核计算
图8给出了参考构型和设计构型的外形对比,其中实线为参考构型即表1中构型15,虚线为设计构型即表3中构型12。为考察设计构型的气动性能,对设计构型从0°到失速迎角附近进行定常N-S方程数值模拟,获得升力曲线,并与基准构型对比。网格总数为35万,计算条件为:Ma=0.2,Re=4.6× 106。

图8 参考构型和设计构型外形对比Fig.8 Shape comparison of the reference configuration with the design configuration
选取如图9所示的控制面作为FW-H方程的可穿透积分面,积分面包括了缝翼与主翼之间的流动区域和后缘涡脱落区域,考虑了四极子噪声源的影响。计算条件为:α=8°,Ma=0.2,Re=4.6×106,非定常时间步长Δt=5×10-5s。
图10给出了设计构型和基准构型的升力曲线对比,可见设计构型和基准构型的失速迎角都为32°,在0°到34°迎角范围内,设计构型的升力系数与基准构型非常接近,甚至略大于基准构型,设计构型的最大升力系数为2.964,大于基准构型的最大升力系数2.906,因此达到了设计目标。

图9FW-H方程积分面Fig.9 Integral surfaces of FW-H equation

图10 设计构型和基准构型升力曲线对比Fig.10 Lift curve comparison of the design configuration with the baseline configuration
图11给出了设计构型和基准构型的压力云图对比,从图中可以看出,相比于基准构型,设计构型由于缝翼凹槽填充的存在,消除了凹槽内大尺度的涡,而大尺度的涡正是气动噪声中低频噪声的主要来源之一。

图11 基准构型和设计构型的压力云图对比Fig.11 Pressure nephogram comparison of the baseline configuration with the design configuration
图12给出了设计构型和基准构型的涡强分布对比,从图中可以看出,基准构型在缝翼凹槽内存在较大的高涡强区域,设计构型不仅使得原本填充区域的涡强消失,更是极大地压缩了高涡强区域。随着高涡强区域的压缩,声源中涡对气动噪声的贡献量也将减小,从而达到降噪的目的。
图13给出了设计构型和基准构型的马赫数分布对比,从图中可以看出,基准构型在缝翼尖端存在剪切层,从而使得气流通过缝翼尖端到达缝道处时,速度增加,在缝道处气流最大马赫数达到0.43左右;设计构型由于缝翼凹槽填充的存在,在缝翼尖端形成了大幅度的连续外形,抑制了剪切层的形成,使得气流达到缝道处时相比于基准构型速度更小,最大马赫数为0.39左右。由于缝道区域气流速度的降低,根据Lighthill理论,这部分气流作为声源,对气动噪声的贡献量也将降低,实现降噪的效果。

图12 基准构型和设计构型的涡强分布对比Fig.12 Vorticity magnitude distribution comparison of the baseline configuration with the design configuration

图13 基准构型和设计构型的马赫数分布对比Fig.13 Mach number distribution comparison of the baseline configuration with the design configuration
图14给出了设计构型和基准构型的湍流粘度分布对比,从图中可以看出,对于基准构型,气流在流经缝翼尖端处后,由于流动的分离,在凹槽和缝道内形成了很大的高湍流粘度区域;设计构型的缝翼凹槽填充,抑制了流动的分离,使得该高湍流粘度区域被大大压缩。从这一点可以看出,由于高湍流粘度区域的减小,湍流作为声源对气动噪声的贡献量也将降低。

图14 基准构型和设计构型的湍流粘度分布对比Fig.14 Turbulent viscosity distribution comparison of the baseline configuration with the design configuration
为考察设计构型的降噪效果,本文对基准构型和设计构型进行气动噪声数值模拟。选取了3个观测点,观测点1位于缝翼后缘点正下方(即270°方向) 20C(C为弦长)处,观测点2位于缝翼后缘点225°方向20C处,观测点3位于缝翼后缘点315°方向20C处。
因为本文选用的设计对象为二段翼,在声源中并没有襟翼噪声的贡献,且所选观测点较远,所以计算所得频谱中声压级较低。图15~图17分别给出了3个观测点处设计构型与基准构型的声压级1/3倍频程频谱对比。在观测点1处,声压级在频率0~3 000 Hz内有明显的降低,当频率高于3 000 Hz时,降噪效果不明显;在观测点2处,声压级在频率0~10 000 Hz内都有明显的降低,降噪效果十分显著;在观测点3处,声压级在频率0~5 000 Hz内都有所降低,尤其是在频率0~300 Hz和1 000~3 000 Hz两个频域内降低明显,当频率高于5 000 Hz时,降噪效果较差。

图15 观测点1处声压级1/3倍频程频谱比较Fig.15 Comparison of 1/3 octave sound pressure level at observation point 1

图16 观测点2处声压级1/3倍频程频谱比较Fig.16 Comparison of 1/3 octave sound pressure level at observation point 2

图17 观测点3处声压级1/3倍频程频谱比较Fig.17 Comparison of 1/3 octave sound pressure level at observation point 3
因此,对于所选取的3个观测点,设计构型实现了降噪的目的,并且降低了声压级峰值。
5 结论
采用定常N-S方程数值模拟考察多段翼型的气动性能,采用CFD(非定常N-S方程)和声类比(FWH方程)相结合的混合方法评估多段翼型的气动噪声。完成了圆柱绕流气动噪声的数值模拟,计算结果与实验值吻合良好,证明了计算方法的可靠性。
为保持多段翼型的气动性能,建立了一个SCF构型的数据库,通过置信度分析,确定了优化设计方向,并以此方向从数据库中挑选出参考构型生成了20个优化构型;以数据库中的构型训练了BP人工神经网络,并以训练好的BP网络预测了20个优化构型的气动性能,从中挑选气动性能最好的构型作为设计构型进行了校核计算。结果显示:所设计SCF构型的气动性能略优于基准构型;对于给定的3个观测点,所设计SCF构型的降噪效果明显,降低了频域内声压级的峰值。
[1] Baldwin T.Overview of Part 36 aircraft noise certification Stages[R].U.S.:LAX/Community Noise Roundtable,2009.
[2] Dobrzynski W.Almost 40 Years of airframe noise research:what did we achieve?[J].Journal of Aircraft,2010,47(2):353-367.
[3] Argüelles P,Bischoff M,Busquin P.European aeronautics:a vision for 2002,meeting society's needs and winning global leadership[R].Luxembourg:Office for Official Publications of the European Communities,2001.
[4] Hileman J I,Spakovszky Z S,Drela M,et al.Airframe design for silent aircraft[R].AIAA 2007-453.
[5] Farassat F,Casper J H.Towards an airframe noise prediction methodology:survey of current approaches[R].AIAA 2006-0210.
[6] Envia E,Thomas R.Recent progress in aircraft noise research[R].U.S.:NASA,2007.
[7] Horne W,James K D,Arledge T K,et al.Measurements of 26%-scale 777 airframe noise in the NASA ames 40-by 80 foot wind tunnel[R].AIAA 2005-2810.
[8] Khorrami M R,Lockard D P,Humphreys Jr W M,et al.Preliminary analysis of acoustic measurements from the NASA-Gulfstream airframe noise flight test[R].AIAA 2008-2814.
[9] Khorrami M R,Lockard D P.Effects of geometric details on slat noise generation and propagation[J].International Journal of Aeroacoustics,2010,9(4):655-678.
[10]Lockard D P,Lilley G M.The airframe noise reduction challenge[R].U.S.:NASA,2004.
[11]Horne W,James K D,Arledge T K,et al.Measurements of 26%-scale 777 airframe noise in the NASA ames 40-by 80 foot wind tunnel[R].AIAA 2005-2810.
[12]Streett C L,Casper J H,Lockard D P,et al.Aerodynamic noise reduction for high-lift devices on a swept wing model[R].AIAA 2006-0212.
[13]Andreou C,Graham W,Shin H.Aeroacoustic study of airfoil leading edge high-lift devices[R].AIAA 2006-2515.
[14]Imamura T,Ura H,Yokokawa Y,et al.Designing of slat cove filler as a noise reduction device for leading-edge slat[R].AIAA 2007-3473.
[15]Shmilovich A,Yadlin Y,Pitera D M.Wing leading edge concepts for noise reduction[C]//Edinburgh,UK:Optimage Ltd.on behalf of the International Council of the Aeronautical Sciences,2010: 5009-5020.
[16] Krist S L,Biedron R T,Rumsey C L.CFL3D User's mannual (Version 5.0)[R].U.S.:NASA,1998.
[17]Mendez S,Shoeybi M,Lele S K,et al.On the use of the fowcs Williams-Hawkings equation to predict far-field jet noise from largeeddy simulations[J].International Journal of Aeroacoustics,2013,12(1):1-20.
[18]Farassat F.Derivation of formulations 1 and 1A of farassat[R].U.S.:NASA,2007.
[19]di Francescantonio P.A new boundary integral formulation for the prediction of sound radiation[J].Journal of Sound and Vibration,1997,202(4):491-509.
[20]Cox J S,Brenter K S,Rumsey C L.Computational of vortex shedding and radiated sound for a circular cylinder:subcritical to transcritical reynolds numbers[J].Theoretical and Computational Fluid Dynamics,1998,12(4):233-253.
[21]Hu G,Liu Z,Xu H N.New extensions of cubic uniform B-spline curve and its applications[J].Computer Engineering and Applications,2008,44(32):161-164.(in Chinese)
胡钢,刘哲,徐华楠.三次均匀 B样条曲线的新扩展及应用[J].计算机工程与应用,2008,44(32):161-164.
Slat cove filler design for noise reduction based on artificial neural network
Tao Jun1,Sun Gang1,*,Xu Kangle2
(1.Mechanics and Engineering Science Department,Fudan University,Shanghai200433,China; 2.Shanghai Aircraft Design and Research Institute of COMAC,Shanghai201210,China)
Airframe noise becomes one of the dominant noise sources during landing and taking off phases of a civil aircraft because that jet engine noise is decreased obviously in recent years.High lift device noise is the main source of airframe noise,decreasing high lift device noise makes a significant contribution to the overall noise reduction for a civil aircraft.Slat cove filler(SCF),as a type of slat noise reduction method,may decrease the aerodynamic performances,such as the maximum lift coefficient and the stall angle.To this situation,a database of SCF is built for a multi-element airfoil,and one of the SCFs in the database is selected as the reference configuration,20 optimized configurations are generated through confidence coefficient reasoning.Aerodynamic performance of each optimized configuration is predicted by a back propagation(BP)artificial neural network,and the one with the best aerodynamic performance is selected as the design configuration for verifying computation,steady Navier-Stokes simulations are executed to compare aerodynamic performances of the design configuration with that of the baseline configuration.A hybrid method,combining CFD with acoustic analogy,is applied to compare the acoustic performances of the design configuration with that of the baseline configuration.The results indicate that the noises are reduced significantly at the given observation points by adding the designed SCF,while the aerodynamic performances have been maintained.
slat cove filler;multi-element;artificial neural network;aerodynamic noise;hybrid method
V211.41
A
10.7638/kqdlxxb-2013.0111
0258-1825(2015)04-0515-08
2013-12-20;
2014-04-08
复旦大学研究生创新基金资助项目(第十一批补充)
陶俊(1989-),男,安徽芜湖人,博士生,研究方向:气动噪声.E-mail:juntao09@fudan.edu.cn
孙刚*(1964-),男,教授,复旦大学.E-mail:gang_sun@fudan.edu.cn
陶俊,孙刚,徐康乐.基于人工神经网络的缝翼凹槽填充降噪设计[J].空气动力学学报,2015,33(4):515-522.
10.7638/kqdlxxb-2013.0111 Tao J,Sun G,Xu K L.Slat cove filler design for noise reduction based on artificial neural network[J].Acta Aerodynamica Sinica,2015,33(4):515-522.
