基于遗传算法双目立体视觉传感器的优化设计

乔德军　张延军　石磊娜

摘 要 为了提高双目立体视觉传感器的测量精度，采用最优回归设计，建立双目立体视觉传感器的结构参数优化模型，并运用遗传算法对建立的优化模型进行求解.通过GA算法的优化，双目立体视觉传感器的测量精度有了较大幅度的提高，优于传统方法的结果.

关键词 双目立体视觉传感器；遗传算法；最优回归设计；种群大小；交叉概率；变异概率

中图分类号 TP39141 文献标识码 A 文章编号 1000-2537（2014）06-0053-04

Abstract In order to improve the measurement accuracy of binocular stereo vision sensor， by using optimal regression design， the structural parameters optimization model of binocular stereoscopic vision sensor is established， which is solved by the genetic algorithm. Measurement precision of binocular stereo vision sensor is greatly improved and better than the result of traditional method.

Key words binocular stereo visual sensor； genetic algorithm； optimal regression design； population size； crossover probability； mutation probability

随着计算机视觉技术的不断发展，视觉传感器得到了越来越广泛的应用，尤其是立体视觉传感器由于原理直观、结构简单、使用方便、测量精度较高、测量速度快等诸多优点，已经大量地应用于工业检测、目标识别、工件定位、机器人引导等领域[1].

双目立体视觉传感器通常由位于同一平面、互成一定角度的两台摄像机组成，其结构参数对其测量精度有直接的影响.目前大多数双目立体视觉传感器的结构搭建是根据人们的经验来选择，结构参数很少有可借鉴的理论依据[2].

为了提高双目立体视觉传感器的测量精度.本文先采用最优回归设计，建立双目立体视觉传感器的结构参数优化模型，再运用遗传算法对建立的优化模型进行求解，从而提高双目立体视觉传感器的测量精度.

1 双目立体视觉传感器参数

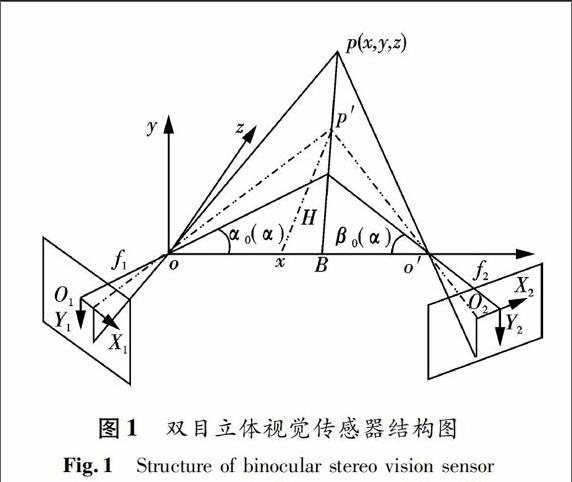
双目立体视觉传感器由两台CCD摄像机组成，如图1所示.两台摄像机水平交向放置，o、o′分别为两摄像机的透视中心，坐标原点设在o点，空间点p（x，y，z）在 xoz 面上的投影为 p′.左右摄像机图像坐标系分别为 O1X1Y1 和 O2X2Y2；经过左像平面中心 O1和透镜中心 o 的直线是左侧摄像机光轴 O1o，经过右像面中心 O2 和透镜中心 o′的直线是右侧摄像机光轴O2o′；两摄像机光轴与基线的夹角分别为 α0 和 β0，两摄像机的透镜中心连线oo′为基线，基线距离记为 B，摄像机的焦距分别为 f1 和 f2，被测物体到基线的垂直距离为 H[3].

据上述分析，双目视觉传感器的结构参数主要包括：两摄像机光轴与基线的夹角、基线距离、摄像机有效焦距和被测物体到基线的垂直距离，它们之间不是独立变化的，而是存在一定约束关系[4].本文中两摄像机对称摆放，两摄像机光轴与基线的夹角相等，即 α0=β0=α，两摄像机的焦距为固定值，选择 f1=f2=25 mm.因此，需要优化的参数为：摄像机光轴与基线的夹角、基线距离和被测物体到基线的垂直距离.

2 最优回归设计模型

根据对双目立体视觉传感器结构图的分析，发现有3个参数需要进行优化设计，因此采用最优回归设计中的311-A方案进行实验.它将3 个因素（即参数x1，x2 和 x3）的不同取值分成 11 个组合，以形成 11 组实验，每组实验中 3 个参数的取值是用编码值来确定的[5-8].最优回归设计 311-A 方案的编码值见表1.

4 遗传算法的双目传感器结构参数的优化

4.1 遗传算法的概述

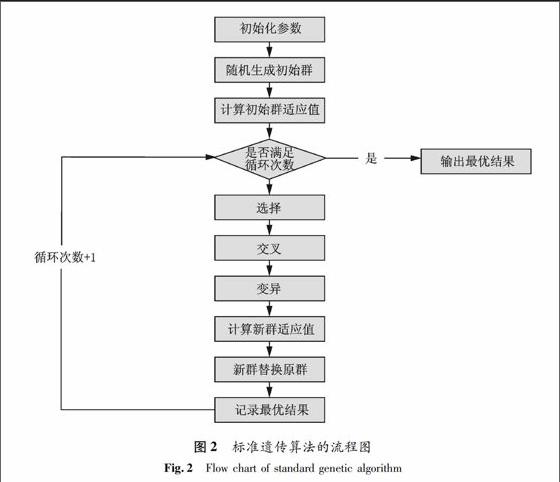
遗传算法（Genetic Algorithm ） 是由美国Holland 教授提出的一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法.它起源于达尔文的进化论， 是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型，其主要步骤如下（图2）：

（1）生成初始种群；

（2）计算初始种群中每个个体的适应度，并判是否符合优化条件.如果符合，则输出相应的最优解，否则执行下列步骤；

（3）根据适应度的大小，选择个体，适应度越高被选中几率越大，反之则可能淘汰；

（4）按照一定的交叉方法和交叉概率Pc执行交叉操作；

（5）按照一定的变异方法和变异概率Pm执行变异操作；

（6）返回上述步骤（2）.

4.3 基于遗传算法的优化

运用Matlab软件，编制遗传算法优化程序，设置相应的参数，初始种群大小为20，交叉概率为0.6，变异概率为0.08，最大遗传代数为1 000.仿真求解得到最优结果：x1=0.066 5，x2=0.287 6，x3=0.991 7，求解结果收敛图如图3所示.

再将最优编码值转化成具体参数，最佳的参数组合为B=41.168，H=31.777，α=57.86°.

根据遗传算法优化后的参数值组合，调节视觉传感器的结构参数，进行验证实验，测得量块的高度值为8.901，比文献[14]中的测量精度有较大提高.

5 结论

为了提高双目立体视觉传感器的测量精度，本文首先采用最优回归设计建立双目立体视觉传感器的结构优化模型，之后运用遗传算法对建立的结构优化模型进行优化，得到最优解，经过遗传算法的优化，双目立体视觉传感器的测量精度有了较大幅度的提高.

参考文献：

[1] 周学斌，杨学友，杨 楠，等. 立体视觉传感器优化设计技术研究[J]. 计算机测量与控制， 2007，15（6）：831-832.

[2] 孙凤梅，黄凤荣，胡占义，等. 视觉测量误差的研究与讨论[J]. 北方工业大学学报， 2005，17（1）：61-63.

[3] 吴彰良，卢荣胜，胡鹏浩，等. 双目立体视觉传感器精度分析与参数设计[J]. 郑州轻工业学院学报：自然科学版， 2006，21（3）：32-34.

[4] 王建华，韩红艳，王春平，等. CCD双目立体视觉测量系统的理论研究[J]. 电光与控控制， 2007，14（4）：94-96.

[5] 张 蕾，徐镜波，杨 丽. 析因试验设计在环境污染物联合毒性研究中的应用[J]. 干旱环境监测， 2004，18（1）：20-22.

[6] 李 伟，朱 红. 均匀实验设计在驱油剂配方研制上的应用[J]. 北京交通大学学报：自然科学版， 2008，32（3）：67-69.

[7] 娄国强，吕文彦. 回归最优设计在麦田杂草防除中的应用[J]. 安徽农业科学， 2006，34（12）：2766-2768.

[8] 刘红波，陆 刚，边 宽. 几种实验设计方法的比较[J]. 安徽农业科学， 2007，35（36）：11738-11739.

[9] 吕桂善，杨志伟，杨正兴. 最优回归设计在食品加工工业中的应用[J]. 广西大学学报：自然科学版， 2001，26（2）：125-126.

[10] 罗宇锋，范耀祖，富 立. 正交设计及D最优设计在陀螺测试中的应用[J]. 压电与声光， 2008，30（4）：393-394.

[11] MONTGOMERY D C. Design and analysis of experiments[M]. 6th ed. New York：John Wiley & Sons Inc， 2004.

[12] 齐力旺，韩一凡，李 玲. 应用 311-A 最优回归设计研究ABA、PEG 4000 及 AgNO3 对落叶松体细胞胚发生数量的影响[J]. 生物工程学报， 2001，17（1）：84-86.

[13] 张雅文，陈梁俊. 最优回归设计在落叶松遗传转化体系主导因子优化筛选试验中的应用[J]. 数学的实践与认识， 2004，34（1）：99-100.

[14] 王以忠，李孝猛.双目立体视觉传感器结构参数优化设计[J].天津科技大学学报， 2010，6（3）：11-14.

（编辑 陈笑梅）