基于自回归模型的基坑周边建筑物沉降预测分析

刘小强

（河南工程学院，河南 郑州 451191）

自回归模型是一种优秀的动态分析方法，可用于预测变化趋势［1］。在模型建立后，需对模型进行检验分析，且必须对模型的预测结果进行验证，以确保其适用性。

1 基坑周边建筑物沉降监测

1.1 基准点

基准点可以埋设在开挖影响区外的原状土中，或在一个稳定的建筑结构上。由于固定的基准点通常用来确定整个沉降监测基准，应该采用高等级的水准网，整个观测也应采用高标准进行。观测应采用高精度的光学或电子水准仪进行。

1.2 精度要求和沉降监测方法

不同的项目和现场条件，对沉降监测的精度要求不同。对基坑周边建筑物沉降监测的目的是为了及时获得沉降信息，并根据其沉降速度确定建筑物是否稳定。沉降速度标准，由设计师或相关规范给出，如某栋建筑物沉降观测，当其沉降量高于0.04mm/d，说明建筑物是不稳定的［2］。因此，要真正确定建筑物沉降量和稳定性，必须使用精密水准测量方法。

2 自回归模型预测方法

假设连续沉降监测样本的平稳序列为

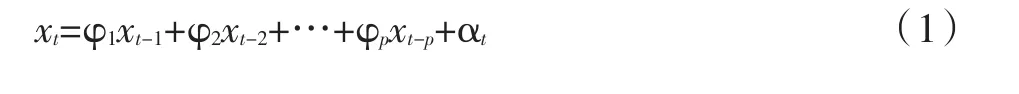
对于时间节点tj和tk，相应的序列是xj和xk。

时间差τ变量之间的自相关函数的估计值可表示为

依据自相关函数，自回归参数φ的估计值可通过方程（3）获得：

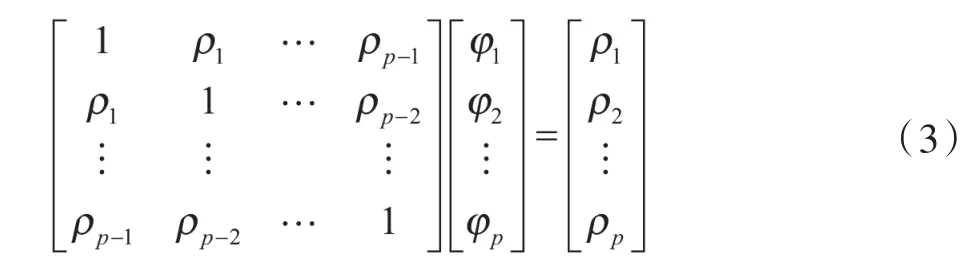
由自回归参数可以确定自回归模型的AR（p）：

根据在时间节点n得到的数据和前期数据，下面的模型可用于预测

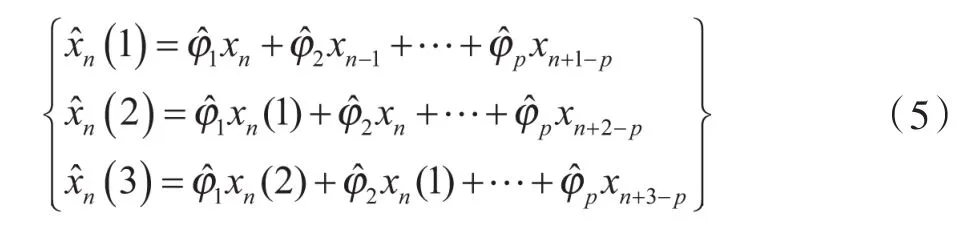
3 沉降预测

实验选择了某深基坑周边的一栋高层建筑物。在远离基坑的外部，选择了三个基准点，形成闭合水准路线。采用二级水准，确定了基准点的数据，且每周对基准点进行稳定性分析。在基坑开挖阶段，对该建筑物连续的进行了沉降监测。表1列出了某一测量点16期的高程观测值。

如表1所示，数值有一些波动，但总的趋势是降低。使用16期的观测数据，估计自相关函数和偏相关函数的前六项，见表2。

如表2中所示，自相关函数的变化没有明显的截尾特征，而偏自相关函数显示了明显的截尾特征，取阈值为0.5，可以确定自回归模型为模型AR（1）。

利用第17-20期的数据进行预测，结果见表3。

如表3所示，使用AR（1）模型预测的最大残差为0.6毫米，表现出良好的精度。说明该自回归模型适用于这座大楼的沉降预测。在整个基坑的施工期，当获得一定量的观测数据后，就可以进行沉降预测。为了提高预测精度，应及时纳入增加的观测数据来校正模型。

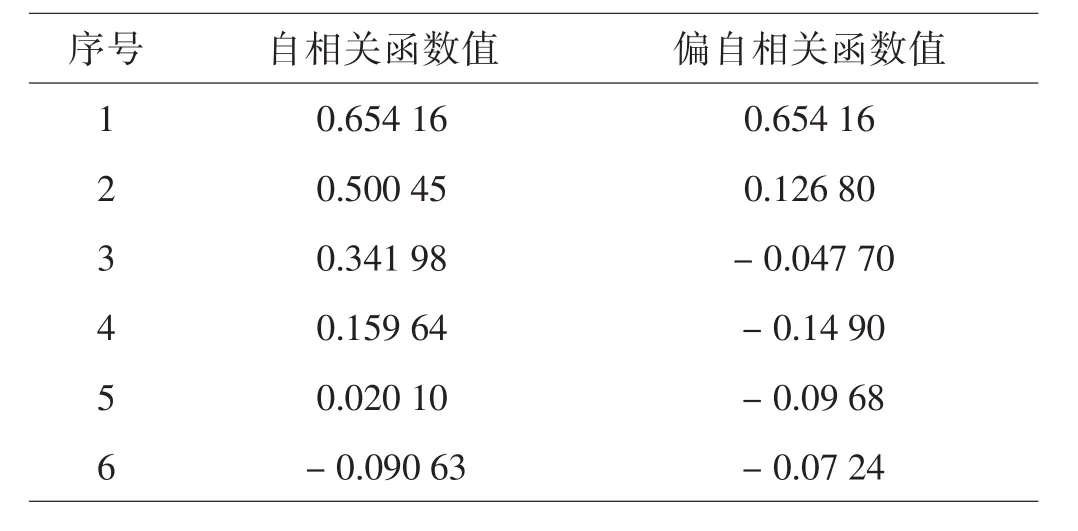
表2 自相关函数值和偏自相关函数值

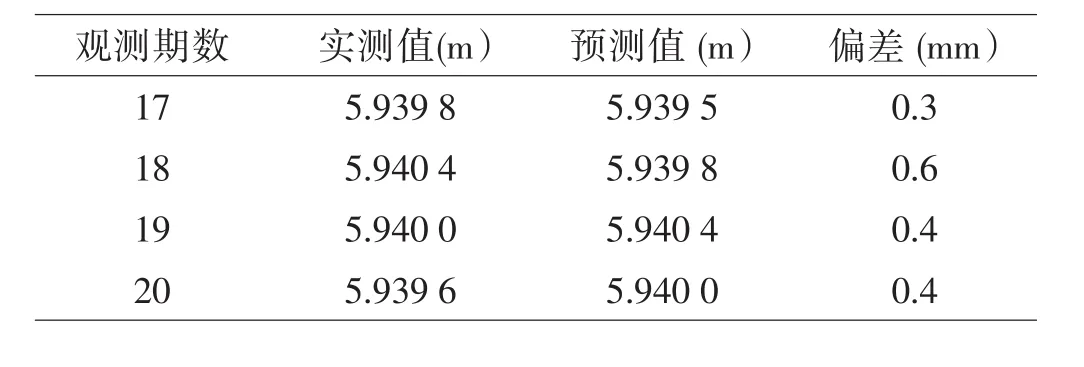
表3 沉降预测结果

4 结语

①应首先用统计检验方法对建筑物沉降监测基准的稳定性进行分析，从而在源头上确保观测数据的有效性。

②为了真实地反映建筑物沉降变化和正确的趋势预测，沉降监测数据的精度必须满足要求。

③构建自回归模型AR（P）必须有相应的样本，且样本的特征需满足相应的要求。一般根据估计的自相关函数和偏自相关函数的特征来确定模型的类型和阶数。对建立的模型必须进行验证，以确保其适用性。

④自回归模型，随着样本的不同模型就会不同，也就是说模型是特定的，不能随意类推使用。

［1］何秀凤，华锡生，等.GPS一机多天线变形监测系统［J］.水电自动化与大坝监测，2002（2）：38-39.

［2］王琪，游新兆，王启梁.用全球定位系统(GPS）监测青藏高原地壳形变［J］.地震地质，1996（12）：121-122.