基于MOS方法建立达州温度预报模型
2015-04-05罗贵东吴海周
罗贵东,吴海周,肖 鹏
(四川省达州市气象局,四川 达州 635000)
基于MOS方法建立达州温度预报模型
罗贵东,吴海周,肖 鹏
(四川省达州市气象局,四川 达州 635000)
利用2009年4月—2010年6月欧洲中心数值预报资料及达州6个国家气象站站温度观测资料,根据影响温度变化的因素和相关分析筛选出了10余个因子,基于MOS方法建立预报模型。在温度预报模型建立上,利用动态最优子集回归,经过多次试验,确定了最低气温和最高气温预报因子。通过2010年1月—2010年 6月与预报员主观预报结果对比分析和7—9月试报检验,预报方法能够有效提高达州温度预报准确率。1—6月检验结果最低气温平均偏小0.31℃,最高气温平均偏小0.53℃。7—9月份试报结果最低气温偏小0.34℃,最高气温偏小0.62℃。
MOS法;动态最优子集回归;温度预报
1 引言
达州市地处区地处亚热带,地形复杂多样,位于四川省东北部,川陕渝交界处,以山地为主,北部处于大巴山腹地,南部是华蓥山、明月山、铜锣山三山构成的川字型地形。复杂地形使其温度变化也有不同于其他地区的特殊性。温度变化对达州的影响也十分巨大,特别是对于农业生产,如2006年的特大高温伏旱和2008年的低温雨雪冰冻灾害给达州造成了巨大的损失。因此高温或低温灾害在某种程度上并不亚于暴雨、干旱等气象灾害的影响。提高温度预报的准确率,是气象更好地为社会经济发展和人们生产生活服务的重要方面,具有很强的现实意义。
目前最常用的温度预报统计方法有神经网络、卡尔曼滤波、回归分析等几种。徐琳娜等[1]以ECMWF数值预报输出产品为基础,对卡尔曼滤波、最优子集回归和岭回归3种方法针对温江、宜宾、内江、达县2005年6—7月的温度预报进行了计算。结果表明:在样本完全相同的情况下,3种预报方法效果相当。在预报方法相同而样本长度不同的情况下,样本长度为 60 d的预报效果较好。赵声蓉[2]基于中国国家气象中心T213模式、德国气象局业务模式和日本气象厅业务模式2 m高温度预报,利用神经网络方法中的BP网络建立了我国600多个站的温度集成预报系统,预报结果检验,表明集成的温度预报结果明显优于3个模式单独的预报结果,72 h内预报的平均绝对误差在3℃以内。王庆国等[3]利用数值预报产品的客观分析场、南宁市单站温、压、湿等资料,建立未来南宁市24 h、48 h、72 h 最高、最低气温的动态因子逐步回归预报方程。张庆奎等[4]用NCEP 格点资料,采用线性插值方法,计算出24 h预报场中各站点850 hPa温度、850 hPa相对湿度和850 hPa垂直速度作为卡尔曼滤波的因子。各站的最低温度预报效果要好于最高温度预报效果,且最高温度和最低温度预报效果夏季要好于冬季。预报结果存在滞后性,尤其当气温变化幅度较大时,明显滞后实况值。陈优平等[5]用GFS数值预报产品和当地地面观测气温资料,采用卡尔曼滤波方法作嘉兴市24 h和48 h日平均气温、 最高气温、最低气温的逐日滚动预报。结果表明:平均气温的预报效果最佳,最低气温次之,最高气温的准确率相对最低;随着时效增长,误差增大;秋季的最高温度误差较小,而冬季则最低气温准确率最高。段荣等[6]利用EC、T213天气数值产品的温度格点实时分析资料、预报资料以及贵州省黔西南州8个测站观测资料,建立了“回归方程预报值+修正值”的分县温度预报方程。回归方程先用相关系数筛选出相关较好因子,然后把这些因子作多元回归统计;订正值根据地理环境,天气形势分型造成的温度差值来确定。方法在应用中取得较好效果,预报误差小于± 3.0℃,平均误差 1.3℃。
2 研究方法与资料
2.1 影响气温变化的因素
由气象学中常用的热流量方程
(1)
可知,影响气温变化的因子主要是温度平流、 垂直运动和非绝热因子,在日常分析某地点气温变化时主要就考虑这三方面的因子。
2.1.1 温度平流的影响 温度平流项是由于气温沿水平气流方向分布不均匀时,空气水平运动所引起的局地气温变化,暖平流使气温上升,冷平流使气温下降。气温变化的程度取决于温度平流的强度,它是一个决定日平均气温的主要因子,同时,温度平流对于气温日变化也有很大的影响,常常会掩盖气温的正常日变化。当强冷空气入侵时,气温明显下降,一直处于负变温,最低气温有可能出现在白天时段。
2.1.2 垂直运动的影响 垂直运动对气温变化的影响,主要与垂直运动的方向、强度以及大气稳定度有关,在一般情况下γd>γ,因而,(γd-γ)RT/Pg>0当出现上升运动时ω< 0,这时温度降低,当出现下沉运动时ω> 0,温度升高。
2.1.3 非绝热因子的影响 气温的非绝热变化是空气与外界热量交换的结果,包括辐射、 湍流交换、 凝结等过程,主要表现在大气低层。影响局地气温变化的主要因子包括云、雾、降水和风等。
2.2 预报统计方法
本文选择的方法为动态最优子集回归。具体的做法就是先利用相关系数检验,筛选预报因子,然后根据这些因子建立多元线性回归方程,方程每天用最近的新样本进行回归分析,经过各种因子组合,选择最优子集回归,确定预报因子。
回归模型中自变量如果太多,会导致信息成本高,模型复杂,计算困难和不易理解分析,而且高度相关的自变量并不增强模型的预测能力,反而加大回归系数的样本变差,削弱模型的描述能力。
多元线性回归中自变量的确定,根据理论知识和经验决定自变量,由于对部分自变量的作用不确认,借助统计分析来实现剔除对问题的研究可能不重要,可能实际上与其他变量重叠以及较大测量误差的因子。选出的自变量数既要足够少,对因变量无重要作用的自变量不能多,也要充分多,对因变量有重要作用的自变量不能少。自变量应选择对因变量作最好预报的一组变量,该组自变量使回归方程拟合得最好。
简单地说最优子集法实际上就是对所有自变量进行组合建立回归模型,然后各模型预报结果和实际结果相比较确定预报误差最小的那一组组合作为最后需要的回归模型。该方法的优点是残差均方最小,F最大,回归方程最优;缺点是如果备选的预报因子较多时计算量很大,如有15个因子则需要215-1个子集回归方程来挑选最优。不能保证引入回归方程的各自变量都有统计学意义、回归方程外的各自变量都无统计学意义。
2.3 资料与数据来源
建立预报方程的资料样本时间为2009年4月25日—2010年6月25日。本文所用的数值预报产品为ECMWF每天08时和20时(北京时 ,下同)的资料 ,空间分辨率为2.5°×2.5°,时间分辨率为24 h。ECMWF资料包括。数据均采用双线性插值法,将欧洲中心的格点预报资料插值到达州市6个站点。方程建立和检验所用的实况资料为达州6个观测站温度资料。如果遇到缺少数值预报资料的样本,该样本舍去不要。
3 预报模型的建立
3.1 相关分析初选预报因子
根据影响气温变化的因素结合本地气候特点,对达州气温变化的主要气象因素选取温度平流、天空状况、大雾和降水,因此我们从欧洲中心数值预报产品中提取与这几大因素有关的因子,并做相关分析。选850 hPa温度以及海平面气压作为反映温度平流的因子;选700 hPa和850 hPa的相对湿度能表征天气活跃区,作为反映云天状况和降水的因子;高度变化与温度变化相关性不好,舍去。最后共确定了欧洲20时和08时850 hPa温度、700 hPa湿度、850 hPa湿度、海平面气压、20时和08时平均温度、平均海平面气压、700 hPa湿度和850 hPa湿度、平均湿度等因子作为数值预报因子。预报当日的最高气温和最低气温作为实况资料预报因子。
3.2 预报方程的因子的确定
根据多元线性回归分析的特点,不是变量越多拟合得越好,当因子数是4~6个时拟合效果一般是最好的,为了减少计算量,结合预报经验我们选取了4~6个因子的各种组合来做回归模型,预报误差最小的回归模型确定为最优的一个组合。徐琳娜等[1]指出气候变化的渐变性对预报结果有较大的影响 ,样本数并不是越多越好,资料样本长度60 d最好。我们在确定预报因子时利用过去60 d的资料样本建立回归模型。
经过大量的计算,对各种因子组合的预报误差进行比较,最后确定最优回归方程子集:
24 h最低气温的预报因子为:预报日前1 d欧洲中心48 h 08时和20时 850 hPa平均温度;48 h 08时和20时平均海平面气压;48 h 08时 850 hPa、700 hPa平均湿度;24 h 08时 850 hPa、700 hPa平均湿度;预报日最高气温;预报日最低气温等6个因子。
24 h最高气温的预报因子为:48 h 08时 850 hPa温度;48 h 20时 850 hPa温度;48 h 08时和20时平均气压;48 h 08时 850 hPa、700 hPa 和20时 850 hPa、700 hPa平均湿度;预报日最高气温等5个因子。

表1 24 h最低气温回归误差排名前3的因子组合
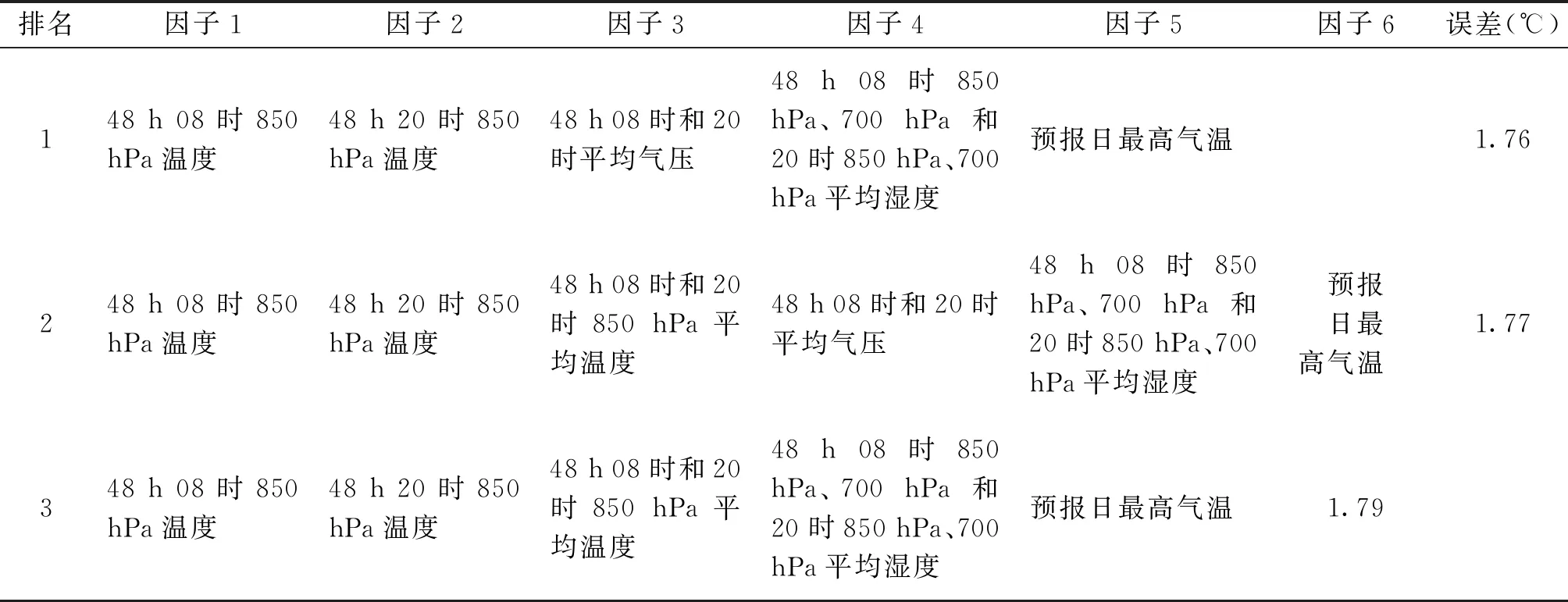
表2 24 h最高气温回归误差排名前3的因子组合
48 h、72 h、96 h、120 h最高、最低气温预报因子和24 h一样,只是数值预报时次不同,需要对应各自的预报时效。
3.3 样本长度的选择
常规的统计方法,都是以大数定律为基础的,即样本越多则预测效果越好,但天气变化存在周期性,如果不考虑年际变化、季节的逐渐转变,利用固定不变的资料建立预报方程,以此为基础进行统计预报,就会带来预报结果很大的误差。因此,需要找出一个相对较好的样本长度,以使建立的预报方程的预报误差最小。我们选择了70 d、60 d、50 d、40 d、30 d 5个样本长度对逐日最低气温、最高气温进行预报试验。
图1是依据5个样本长度对2009年4月25日—2010年6月25日全市6个站点24~120 h日最低、最高气温预报值进行绝对误差统计的平均结果。从中可见,几个样本长度下,预报效果差别不大,最低气温误差在1.49~1.56℃之间,最高气温误差2.31~2.33℃之间,不同样本数之间的差值在0.1℃以内。最低气温30 d误差最大,为1.56℃;60 d误差最小,为1.49℃。最高气温30 d、50 d天误差均为3.33℃;60 d误差最小,为2.31℃。因此,最后确定建立预报方程的样本数量为60 d。

图1 不同样本数量绝对误差
3.4 回归系数的计算
回归模型中预报因子已经确定,但是回归系数并不是固定的,而是每天加入新样本重新统计。如何做到系数的动态变化,每天我们取预报日前60 d资料为统计样本建立回归方程,这样预报方程回归系数可以根据时间的变化不断修订,从而提高下一时刻预报精度。这也避免了用固定回归系数时,当今后数值预报结果精度提高,预报反而不准确的问题。
该方法在保证预报准确率的前提下,更容易和VB、EXCEL结合,具有编程简单、使用方便的特点。在实现预报自动运行中主要用到了VBA技术,用EXCEL中的linest函数便可以进行多元回归统计,计算出温度预报结果。这里linest函数作用就是应用最小二乘法建立回归方程(公式4)。
3.5 预报误差分析
3.5.1 时效误差 从图2可以看出温度预报的准确率与预报时效长短成反比,时间越长,误差越大。最低气温平均绝对误差,24 h最小,为1.22℃;120 h最大,为1.64℃。最高气温平均绝对误差,24 h最小,为1.76℃;120 h最大,为2.66℃。不论是哪一个时次的预报,最高气温误差始终大于最低气温误差,这可能是最高气温波动更大的缘故。

图2 各预报时效平均最低、最高气温绝对误差
3.5.2 季节误差 从图3可以看出最低气温绝对误差,夏季最小,为0.99℃,春季最大,为1.80℃,总的来说夏半年误差小于冬半年。最高气温绝对误差,冬季最小,为1.94℃,夏季最大,为2.49℃,总的来说冬半年误差小于夏半年。春季最低气温误差最大、夏季最高气温误差最大,其原因是由于春季最低气温波动更大,夏季最高气温波动更大。另外,夏季最低气温准确率1~5 d都很高,误差在0.8~1.13℃之间,这也说明夏季最低气温波动较小。

图3 各季节平均最低、最高气温绝对误差(单位:℃)

表3 达州各站最低气温预报绝对误差 (单位:℃)
3.5.3 地区误差 从表1和表2可以看出,1~5 d平均绝对误差,最低气温预报大竹最小,为1.36℃,开江最大,为1.68℃;最高气温预报开江最小,为2.21℃,渠县最大,为2.37℃。
3.5.4 与预报员主观预报结果对比分析 为了便于业务应用和比较,这里客观预报结果首先四舍五入到整数。通过对达州市2010年1—6月,1~5 d预报员主观预报质量检验结果和本研究客观预报报结果对比分析可以看出:研究取得了较为明显的成果,1~5 d最高、最低气温预报误差均比主观预报要小,最低气温平均偏小0.31℃,最高气温平均偏小0.53℃,见表3,表4。通过对比分析说明课题研究成果可以有效减小温度预报误差,提高达州市温度预报能力。

表4 达州各站最高气温预报绝对误差 (单位:℃)

表5 2010年1—6月最低气温预报对比 (单位:℃)
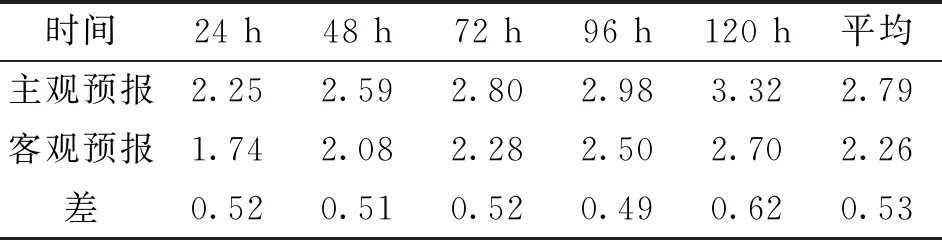
表6 2010年1—6月最高气温预报对比 (单位:℃)
3.5.5 强降温天气预报效果 2009年10月—2010年4月,出现的区域性强降温天气过程有2009年11月11—13日,2010年3月21—24日,2010年4月11—14日,其中3月21—24日全市气温平均下降13.2℃,另外两次过程降温幅度分别为8.2℃、7.9℃。
从3次强降温过程的预报情况来看:强降温时最低气温误差明显大于最高气温误差,这与总体的误差情况正好相反;最低气温预报绝大多数时候预报偏高,3次过程平均预报误差偏高3.0℃,根据这个特点,在预计将会发生较强降温的时候,预报员可以将最低气温预报值调低3℃左右;最高气温预报大多数时候预报也是偏高,3次过程平均预报误差偏高1.4℃,根据这个特点,在预计将会发生较强降温的时候,预报员可以将最高气温预报值调低1℃左右;预报方程提前2~3 d对降温过程做出的预报已经具有较好的指导作用,最低温度预报时效长短和预报误差大小的相关性不大,最高温度预报误差时效越长,误差越大。

表7 强降温过程最低、最高温度预报误差 (单位:℃)
3.5.6 误差原因分析 温度预报产生误差的原因:一是,尽管欧洲中心数值预报是众多数值预报产品中预报效果较好的,但其预报值肯定还是存在一定的误差,那基于其产品制作的温度预报也就必然会存在一定的误差。二是,天空状况对温度有很大的影响,虽然数值预报因子中高空湿度对天空状况有一定指示意义,但很难准确反映出局地的天空状况变化情况,从而导致预报出现偏差。三是在温度出现较大波动时,线性回归的平滑特性会减小温度波动,从而导致温度预报变化的幅度偏小。四是运用的数值预报产品的精细化程度不够高,时间分辨率为12 h,空间分辨率为2.5°,这就不能完全反映出现最低最高气温时预报站点所在地的大气情况。五是,短时的天气变化对温度影响较大,如阵雨等。本文所运用的数值预报产品反映的主要是大的环流形式,还无法预报短时局地天气过程,而这些天气对温度的影响也至关重要。
最高气温误差较大的原因:一是由于最高气温波动较最低气温波动更大,线性回归平滑特性会减小这种波动。二是最高气温一般要先经历最低气温后再出现,根据蝴蝶效应,微小的初始值变化,可能会引起后面巨大的变化。三是天空状况变化对最高气温影响更为显著,特别是午后,这是一般是最高气温出现的时段,而这时空气又是一天中最不稳定的时候,云的发展将对最高气温产生较大影响。
3.6 业务试验效果
2010年7—9月对温度预报平台进行试运行,结果显示:温度试报结果较预报员主观预报有明显的提高,除了24 h最高温度预报误差比主观预报大外,其余均较主观预报要小,5 d平均最低温度预报误差减小了0.34℃,最高温度预报误差减小了0.63℃。
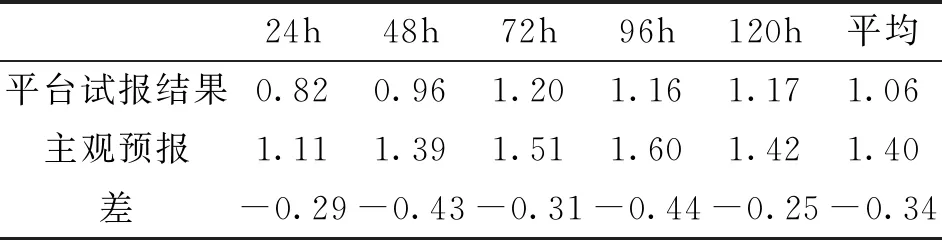
表9 2010年7—9月最低气温预报对比 (单位:℃)

表10 2010年7—9月最高气温预报对比 (单位:℃)
4 结论
①客观的温度预报方法能够明显的提高预报员温度预报的准确率。从1—6月检验结果1~5 d平均误差最低气温为1.49℃,最高气温为2.31℃,最低、最高气温预报误差均比主观预报小,最低气温平均偏小0.31℃,最高气温平均偏小0.53℃。7—9月份试报结果也表明预报平台温度预报误差也较预报员主观预报小,最低气温偏小0.34℃,最高气温偏小0.62℃。
①预报误差与温度波动幅度成反比,当温度比较稳定时准确率较高,这与线性回归本身的特性有关。因此夏天最高气温预报误差最大,而最低气温误差又最小;冬季最高气温预报误差最小,春季最低误差最大;最高气温预报大于最低气温。
③温度预报的准确率与预报时效长短成反比,时间越长,误差越大。
④在有明显降温天气过程出现,可以加入预报员的经验订正,或者是加入不同天气系统形式下的订正预报值,这样利于温度预报误差的进一步缩小。
⑤存在的不足。方法比较单一,还能进一步丰富,下一步可以采用不同方法和不同的数值预报产品,实现几种方法和几种模式的集成预报,这样温度预报的准确率可能还会有一定提升。在缺少欧洲中心数值预报资料时,无法做预报,因此要尽量保证每天资料的完整。最高气温预报还有较大难度,需进一步研究。
[1] 徐琳娜,冯汉中.基于数值预报产品的温度释用方法比较[J].四川气象,1998, 96 (2):3-7.
[2] 赵声蓉.多模式温度集成预报[J].应用气象学报,2006,17 (1):52-58.
[3] 王庆国, 黄归兰, 李广海.南宁市温度预报的动态因子逐步回归方法研究[J].广西气象,2006,27 (增刊1):51-53.
[4] 张庆奎,寿绍文,陆汉城.卡尔曼滤波方法在极端温度预报中的应用[J].科技信息,2008(35):51-53.
[5] 陈优平,陆琛莉,李云泉.基于GFS产品和卡尔曼滤波的嘉兴市温度客观预报[J].气象科技,2009,37 (2):141-144.
[6] 段荣,李莉群,何海燕,等.利用天气数值预报产品建立贵州黔西南州分县温度预报方程的方法及应用[J].云南地理环境研究,2007,19(增刊):67-70.
2015-02-03
罗贵东(1980—),男,工程师,主要从事天气预报及气象服务工作。
1003-6598(2015)04-0016-06
P423
B
