SWAN定量降水估测和预报产品在贵州乌江流域的应用
2015-04-05唐延婧
宋 丹,熊 伟,唐延婧
(1.贵州省气象服务中心,贵州 贵阳 550002;2.贵州省气象信息中心,贵州 贵阳 550002)
SWAN定量降水估测和预报产品在贵州乌江流域的应用
宋 丹1,熊 伟2,唐延婧1
(1.贵州省气象服务中心,贵州 贵阳 550002;2.贵州省气象信息中心,贵州 贵阳 550002)
该文选取乌江流域范围内出现区域性降水达到中雨以上量级的1 h降雨资料,再运用同期SWAN系统中定量降水估测(简称QPE,下同)和定量降水预报(简称QPF,下同)产品,计算贵州乌江流域范围内面雨量,对其进行误差订正及检验分析。结果表明:定量降水估测和定量降水预报的效果不好,经过误差订正后的QPE和QPF更加接近于实况;订正后的QPE的相对偏差在30%左右,而QPF多在40%~60%之间浮动;QPE和QPF经过二次订正后,与实况基本一致,具有更高的估测与预报能力,可应用于实际业务中。
SWAN系统;降水估测预报;相对偏差;订正偏差;贵州乌江流域
1 引言
乌江是长江上游南岸最大支流,发源于贵州省威宁县香炉山花鱼洞,流经黔北及渝东南,在重庆市涪陵区注入长江,是贵州的第一大河。乌江水能蕴藏丰富,沿流域建有近10座水电站,发电量占贵州全网的70%左右。流域内降水偏多,可使水库水位上涨,甚至引发洪涝,严重影响电站的安全发电和电网的正常运输;降水偏少,水库水位过低,会降低发电量水平,对西电东输工程造成严重影响。
短时强降水因突发性、局地性强,其造成的灾害和损失尤为严重。因此做好流域内短时临近定量降水估测和预报,对开展流域气象防灾减灾服务以及避免或减轻由短时强降水造成的经济和生命财产损失具有特殊意义。灾害天气短时临近预报预警业务系统(简称“SWAN”)是应用雷达、自动站、危险天气报、模式等数据,针对突发性强的短时强降水和强对流天气,优选全国各地开发的算法和研究成果,检验、集成并加以优化优选,基于MICAPS3平台建设的一个快速反应、业务化、强降水和强对流天气监测预警和临近预报为一体的灾害性天气综合分析与临近预报业务平台[1]。随着SWAN系统的业务化,国内学者针对SWAN系统的应用分析研究逐渐增多,基于雷达产品的特征及其在强对流天气预报预警和分析中的应用[2-4];吕晓娜等[5]分析了SWAN系统中QPE和QPF产品在河南短时强降水过程中的误差分布,并讨论了二者在局地强降水过程中的差别及产生误差的原因,表明了QPE和QPF对低于10 mm/h的降水有较好估测和预报能力。
贵州省对SWAN产品的应用检验分析几乎没有,乌江流域区域范围内对降雨强度的敏感性较大,因此,本文将对SWAN的定量降水估测(雷达估测1 h降水量,QPE)和定量降水预报(QPF)产品在乌江流域的应用效果进行误差订正及检验,以改善估测和预报值偏低的问题,以期将SWAN产品的应用达到最佳效果,为更好地利用SWAN系统对贵州省灾害性天气进行短时临近天气预报服务提供参考。
2 资料和方法
2.1 资料说明
从区域自动站数据库中提取2014年3—8月中雨以上量级的逐小时降雨量、经纬度信息,提取乌江流域范围内的站点,作为实况雨量,乌江流域经纬度范围在26~29°N、104~109°E之间。由于自动站为离散点,需进行插值处理。任意格点,取其半径≤5 km的所有雨量站的平均值作为该点的雨量值。
在SWAN服务器端配置贵州Z—R关系(Z表示雷达反射因子,R表示降雨强度),输出整点QPE和QPF产品,选取与实况相同时次资料,并提取乌江流域范围内数据,起点经纬度坐标为(29°N,104°E),终点坐标为(26°N,109°E),分辨率为0.01°×0.01°,约为1×1 km。
2.2 误差订正方法
误差订正主要采取点面结合的方式,利用乌江区域内所有自动站每小时雨量资料(离散点),对QPE/QPF值进行误差订正。首先将自动站雨量插值到格点,得到一个格点场,然后利用此格点场去订正QPE/QPF值。离散点的插值技术是采用Cressman客观分析方法[8],最后利用变分校准法对QPE/QPF进行订正。
在网格点(i,j)上,QPE/QPF值为PSr(i,j),自动站雨量经过Cressman插值到格点的雨量为PSg(i,j)(QPE对应同一时次,QPF对应前一时次),订正因子为自动站雨量减去QPE/QPF值,公式:
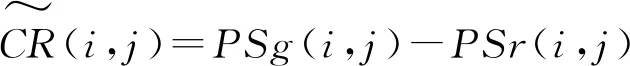
(1)
在每一网格点(i,j)上,订正因子的实测值CR(i,j)和分析值(i,j)之差的平方和为
(2)
经相关数学分析推导最后得到欧拉方程:
(3)
式中α称为观测权重,λ也像观测权重α一样,是事先给定的,称为约束权重。采用超松弛跌代法解式(3),得到订正因子场CR(i,j),可知经变分校准后,网格点(i,j)上QPE/QPF值为:
PS(i,j)=PSr(i,j)+CR(i,j)
(4)
利用(4)式即可得到订正后的QPE/QPF值。
2.3 检验方案
通过计算流域面雨量对SWAN系统中QPE/QPF产品进行检验分析。定义3类面雨量:
①估测面雨量Re:在500×300的格点中,有40 000个格点在乌江流域范围内,将流域内的格点雨量求平均值,得到估测流域面雨量。
②预报面雨量Rf:计算方法同Re。
③订正后面雨量Rc:将经过误差订正后的格点降水量,计算流域面雨量。
④实况面雨量R:流域内所有自动站雨量的平均值。
利用相对偏差和订正偏差来对Re/Rf和Rc进行检验。相对偏差σr为面雨量估测/预报值的绝对偏差占实况值的百分比,用来衡量单次估测值对实况值的偏离程度,公式(式中Re可替换成Rf和Rc):
(5)
订正偏差(σc)为订正后面雨量的绝对偏差占订正后面雨量的百分比,公式:
(6)
3 QPE误差订正和检验分析
3.1QPE订正前后与实况对比3.1.1 单次降雨过程区域对比 图1为2014年3月19日21时QPE产品订正前后与实况雨量对比区域图。从图1中可以看出,QPE订正前与实况有一定差异,虽然降水落区比较接近,但对此次过程乌江流域上出现的10mm以上降水未能估测出;经过订正后的QPE与实况不仅落区一致,并且也能估测出降水区南部的10mm以上降水。因此,这种点面结合的方式得到的面上的降水还是较为合适的。
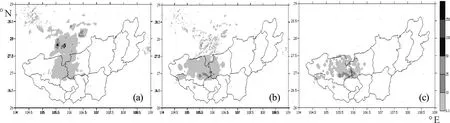
图1 QPE订正前后与实况雨量对比(a.订正前;b.订正后;c.实况)
3.1.2 降雨过程序列对比 图2为所选取的272个例的估测面雨量、订正后面雨量和实况面雨量的序列对比图,88.6%的个例Re比R和Rc小,96.3%的个例订正前后面雨量比实况面雨量都要小。从面雨量的个例变化形态来看,其波峰和波谷的位置较为一致,说明估测面雨量有较好的指示意义,而经过订正后的面雨量不仅趋势一致,且比估测面雨量更接近于实况。

图2 估测面雨量、订正后面雨量和实况面雨量对比序列
3.2QPE相对偏差
为更进一步了解订正前后的面雨量跟实况之间的误差,将R分为3个等级:R<1mm,量级定义为中雨,112个例;1mm≤R<2mm,量级定义为大雨,99个例;R≥2mm,量级定义为暴雨,61个例。根据公式(5)分别计算不同等级下订正前后面雨量的相对偏差。从图3看出,订正后面雨量和估测面雨量的相对偏差多为正值,说明比实况值小,但是订正后的相对偏差明显比订正前的小,说明订正后面雨量偏离实况的程度较订正前小。不同等级订正后面雨量的相对偏差变化起伏不大,基本在30%附近上下浮动,而估测面雨量变化起伏明显,且偏差较大。从表1可知,3个等级订正后的相对偏差平均值为28%左右,而订正前的平均值在54%~60%之间;中雨等级订正前后的最大振幅大于其它2个等级的,暴雨等级的相对偏差的振幅反而最小,说明降雨量级越大,订正前后的相对偏差变幅范围越窄,越稳定。

图3 不同等级订正后和估测面雨量的相对偏差
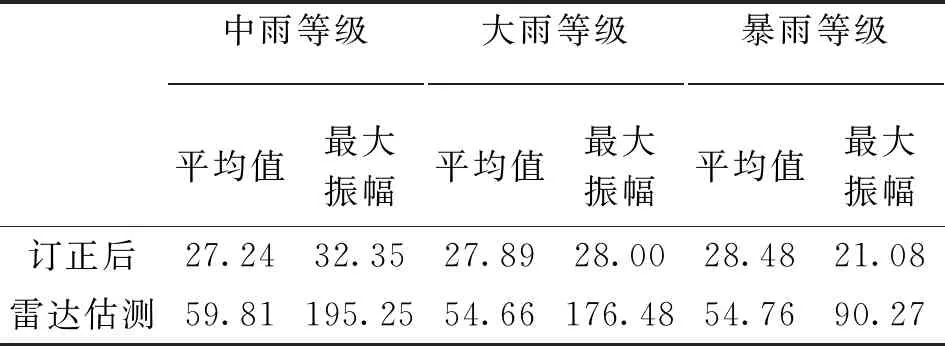
表1 不同等级订正后和估测面雨量的相对偏差的平均值及最大振幅 (单位:%)
基于以上特征,为得到更接近于实况的Re,以订正后面雨量上浮实况面雨量的30%作为估测面雨量结果。
3.3QPE订正偏差
在实况面雨量未知的情况下,引入订正偏差。根据公式(6)分别计算272个例的订正偏差,计算其平均值和最大振幅(见表2)。从表2可看出,不同等级的订正偏差约在40%左右,且雨量越大,偏差越大,而其最大振幅表现为雨量越大,偏差变化幅度越小;对比表1中的数据来看,订正偏差的平均值与振幅均大于相对偏差的。

表2 不同等级订正后面雨量的订正偏差的平均值及其最大振幅 (单位:%)
将订正后的面雨量上浮40%后得到接近于实况的面雨量,并与实况面雨量进行对比分析(见图4),订正上浮后面雨量与实况面雨量基本重合,说明对估测面雨量的二次订正方法可行并且效果很好。
4 QPF误差订正与检验分析
4.1 预报与实况对比
图5为所选取的245个例QPF的预报面雨量、误差订正后的预报面雨量和实况面雨量的对比序列。从图5看出,Rf较R和Rc明显偏小,几乎都接近于0,说明未经过订正的预报面雨量无法预测中雨以上量级的降水。经过误差订正后的面雨量预报更接近于实况,但仍小于实况值,并且当实况出现2mm以上的面雨量时,绝对误差明显增大。
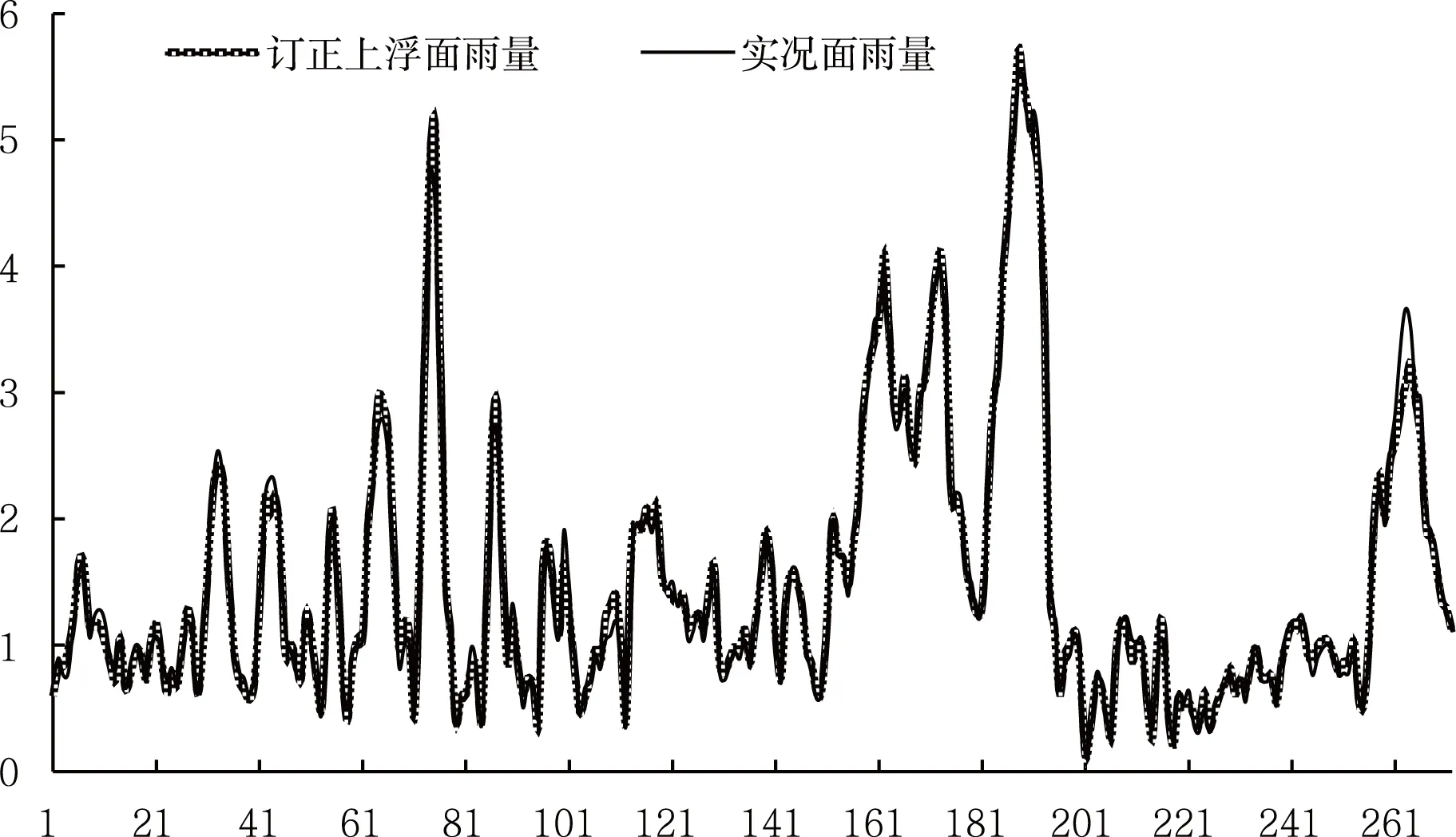
图4 订正上浮估测面雨量和实况面雨量的序列对比

图5 预报面雨量、订正后预报面雨量和实况面雨量对比序列
4.2QPF相对偏差和订正偏差
通过计算订正后预报面雨量的相对偏差和订正偏差可以看出(图6),相对偏差变化幅度多在40%~60%之间,平均为50%左右,说明实况为订正后预报面雨量的两倍。从订正偏差的分布来看(已去掉4个异常极大值),其浮动很大,多在50%~200%之间,计算低于250%的订正偏差的平均值约为105%。将订正后预报面雨量上浮1.05倍后与实况值进行对比分析(图7),可看出订正上浮后的面雨量预报与实况基本接近,尤其是在实况面雨量相对较大时,其趋势和值几乎重合,而面雨量相对较小时,其变化并不完全一致,但差异也不算大,对预报效果影响不大。实际上也可以通过相对偏差来进行订正,将订正后预报面雨量乘以2,结果相差不大。因此,对上浮后的订正预报面雨量基本能反映实况值,对业务服务也具有较高的指示意义。
5 小结与讨论
本文就乌江流域范围内的SWAN中定量降水估测和定量降水预报进行误差订正及检验分析,得到如下结论:
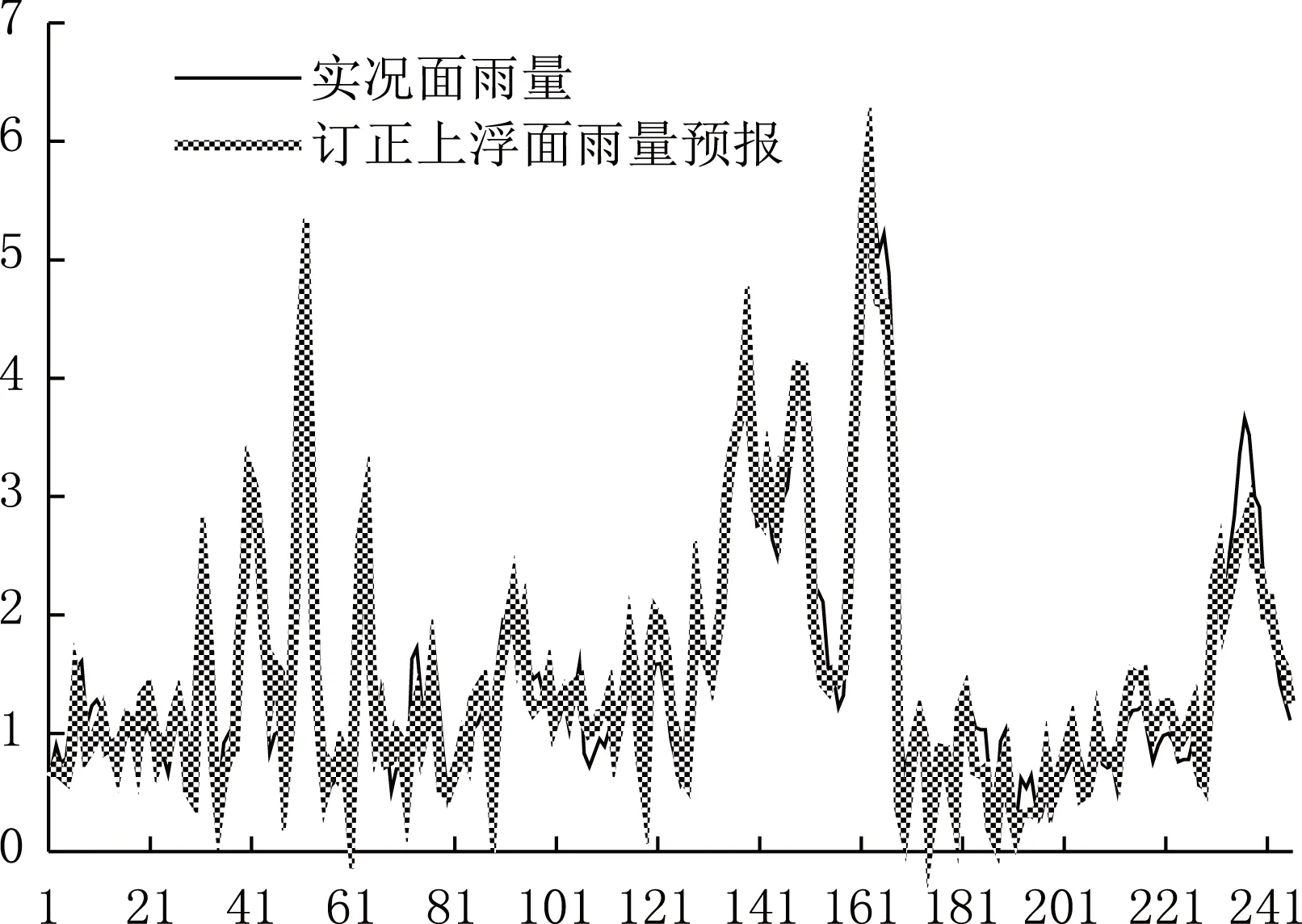
图7 订正上浮面雨量预报与实况对比序列
①对于中雨以上量级的降水,定量降水估测和定量降水预报的效果不理想,不能直接应用到实际业务中,经过误差订正后的QPE和QPF更加接近于实况。
②经过误差订正后的QPE的相对偏差在30%左右,订正偏差约为40%,将订正后的QPE进行2次订正上浮40%后,与实况基本一致。
③经过误差订正后的QPF的相对偏差多在40%~60%之间浮动,订正偏差波动更大,平均约为105%,将订正后的QPF进行2次订正上浮1.05倍后,与实况基本一致。
④QPE和QPF的2次订正效果较好,可应用于实际业务工作中。
[1] 胡胜,罗聪,黄晓梅,等.基于雷达外推和中尺度数值模式的定量降水预报的对比分析[J].气象,2012,38(3):274-280.
[2] 吴涛,万玉发,沃伟锋,等.SWAN系统中雷达反射率因子质量控制算法及其应用[J].气象科技,2013,41(5):809-817.
[3] 傅朝,闫晗,刘维成,等.SWAN雷达产品在甘肃河东地区冰雹短临预报中的应用[J].干旱气象,2013,31(1):199-205.
[4] 陈永仁,李跃清.基于SWAN产品的短时强降水雷达特征及预警分析[J].高原山地气象研究,2013,33(1):72-79.
[5] 吕晓娜,牛淑贞,袁春风,等.SWAN中定量降水估测和预报产品的检验与误差分析[J].暴雨灾害,2013,32(2):142-150.
2015-01-07
公益性行业(气象)科研专项(GYHY201306059)资助。
宋丹(1982—),女,工程师,主要从事天气预报及相关研究工作。
1003-6598(2015)05-0024-04
P457.6
B
