基于频率反演结构刚度
2015-04-03余建波黄怀英刘庆彬
胡 豪,余建波,黄怀英,刘庆彬
(中航工业洪都,江西 南昌330024)
对于实际的结构,在建立有限元模型时,总避免不了铆钉、螺栓连接,而连接的松紧程度对结构的刚度有着显著影响,且对于连接刚度,有限元往往无法直接建立模型。所以,需要通过相应的模态试验,确定结构的模态参数。然后利用模态参数,调整有限元模型中相应的连接刚度,使有限元计算的模态参数尽可能与试验相符。国内外有很多学者致力于反问题的研究。Starek和Inman[1-2]通过特征值反演系数矩阵;Cheng-Hung Huang[3]利用共轭梯度法反演了多自由度系统瞬态问题中随着时间变化的外力;高效伟、崔苗等使用边界元法反演了导热参数。
本文针对集中质点的多自由度系统的振动问题,通过部分测试频率反演系统的刚度。
1 动力学方程
多自由度系统振动方程:
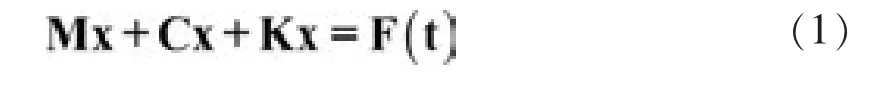
矩阵M,C和K分别是质量,阻尼和刚度矩阵。那么对应的无阻尼系统的固有频率满足方程:

求解方程(2)即可以得到多自由度系统的频率,进而得到系统的振型。对于反问题,系统的部分刚度因未知而无法直接求解。因此,需要建立适当的反演模型,反推出系统的连接刚度。通过模态试验,可以获得多自由度系统低阶的模态。本文使用低阶的模态数据反演结构刚度。
2 优化方法
对于非线性最小二乘问题,有:

假定初始点x0经过k次迭代得到xk,把 fi(x)在xk点处展开成一阶Taylor表达式:
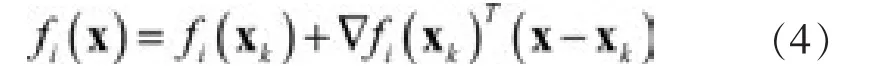
根据f(x)的Jacobi矩阵:

可以得到:
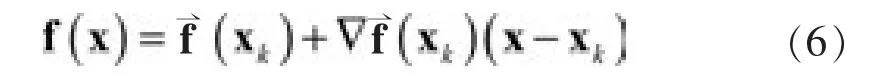
从而:
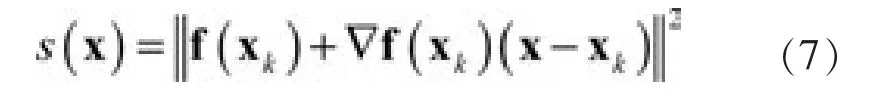
所以,最终得到线性最小二乘问题:
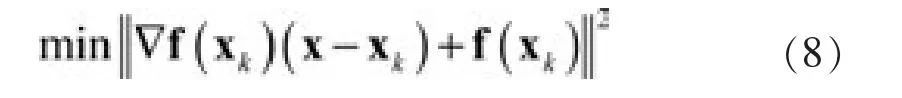
于是,得到最优解xk+1满足下面的方程组,即:
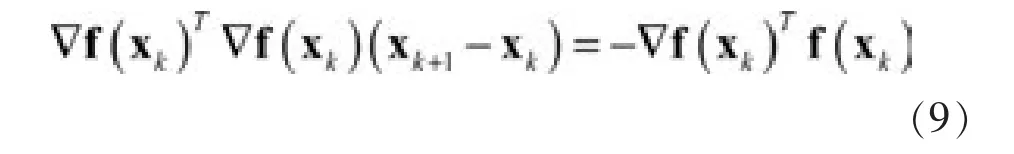
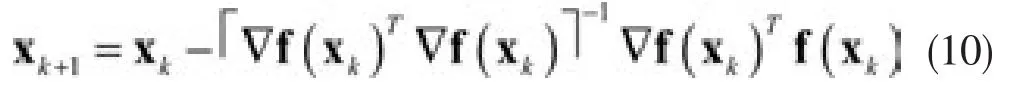
上式称为Gauss-Newton公式,向量:
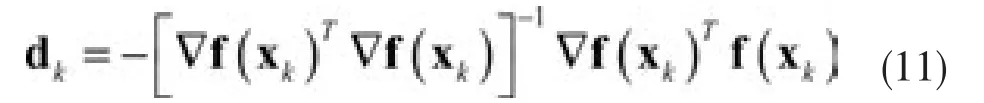
称为Gauss-Newton方向,其中灵敏度矩阵为
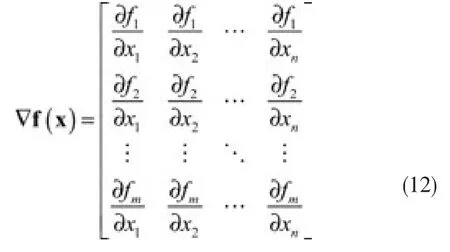
3 复变量求导法
对于任一实函数f(x),将所求导变量x施加一个很小的虚部h(通常是很小),并将其展开成Taylor级数得:
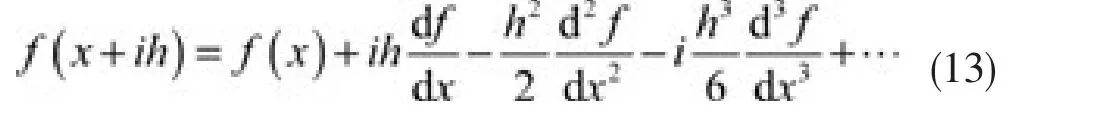
于是,一阶导数:
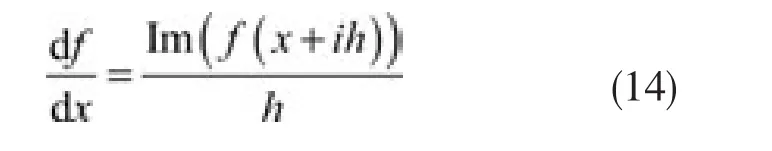
二阶导数:

优点:
1)一阶导数利用各自虚部的比值,没有相消误差,极大地提高了差分的数值计算精度。在计算复杂函数的导数时,差分步长可以取的很小。
2)能利用正算程序进行反分析。
4 数值算例
考虑一个具有10个质点的多自由度动力学系统见图1,其中每个质点的质量和弹簧的刚度见表1。
上述系统前 5阶的固有频率分别为8.3814、52.5387、130.492、233.115和340.973.现在假定k1、k7是未知的。利用第1、3、4阶频率反演。
1)利用第1、3、4阶频率反演k1、k7,给定初始迭代点k1=1300、k7=2300,迭代结果见图2。
反演结果表明,通过1、3、4阶频率可以识别动力系统的刚度系数k1、k7,迭代10次以后反演解趋近精确解。
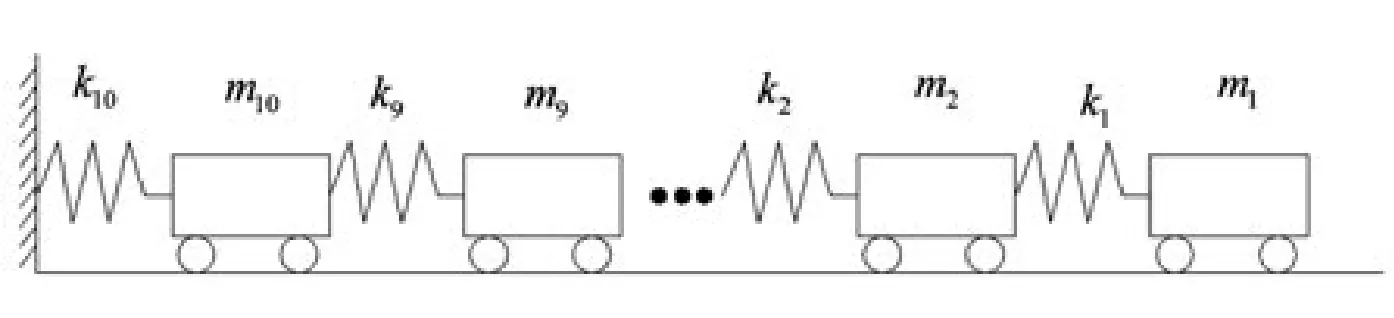
图1 10个质点的多自由度动力系统

表1 每一个质点的质量和弹簧的刚度
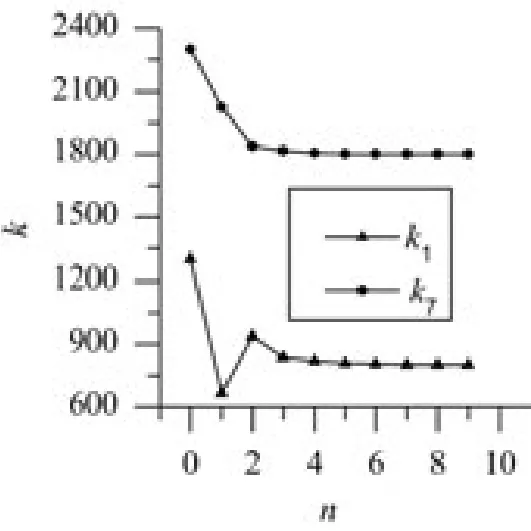
图2 利用1,3,4阶模态反演刚度迭代过程
2)利用第1、2、3阶频率反演k1、k7,给定初始迭代点k1=1300、k7=2300,迭代结果见图3。
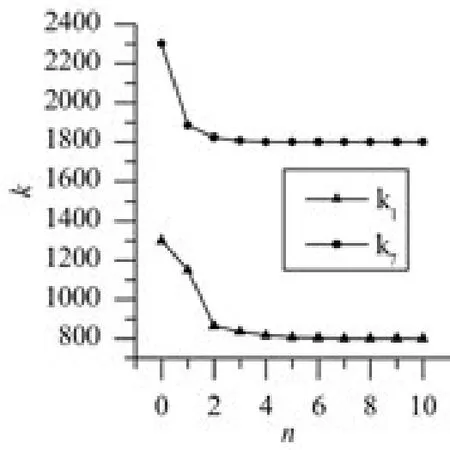
图3 利用1,2,3阶模态反演刚度迭代过程
反演结果表明,通过1、2、3阶频率可以识别动力系统的刚度系数k1、k7,迭代10次以后反演解趋近精确解。
5 结 语
本文对一个多自由度系统建立了反演分析模型。数值计算的结果表明了反演模型的正确性和有效性。通过低阶的模态数据可以同时反演系统的多个连接刚度。
[1]L.Starek,D.J.Inman,On the inverse vibration problem with rigid-body modes,Trans.Am. Soc.Mech.Eng.,J.Appl.Mech.58(1991)1101-1104.
[2]L.Starek,D.J.Inman,A.Kress,A symmetric inverse vibration problem,Trans.Am.Soc.Mech.Eng., J.Vib.Acoust.114(1992)565-568.
[3]H cheng-hung,A generalized inverse force vibration problem for simultaneously estimating the time-dependent external forces.Applied Mathematical Modeling 29(2005)1022-1039.
