滚仰式光学滑环的测角分析

胡恒松，丁海山，花文涛，赵桂瑾, 2



滚仰式光学滑环的测角分析

胡恒松1，丁海山1，花文涛1，赵桂瑾1, 2

（1. 中航工业空空导弹研究院，河南 洛阳 471009；2. 航空制导武器航空科技重点实验室，河南 洛阳 471009）

滚仰式光学滑环被广泛应用在小型化位标器中。由于引入了折转光路，其对目标的空间角位置测量比传统的跟踪成像系统更复杂。基于光线反射定律和等距变换理论研究滚仰式光学滑环对目标的空间角位置测量，得到理论计算公式和近似计算公式，最后通过数值仿真验证了分析结果的正确性。

光学滑环；滚仰；空间角位置；等距变换；稳定平台

0 引言

为了适应低成本和小型化的要求，滚仰式半捷联位标器成为研究的主要方向[1]。这种位标器在结构上和传统的速率陀螺稳定平台式位标器有很大不同。传统的位标器是将探测器和光学系统作为整体直接安置在稳定平台上，目标红外辐射沿着直线光路入射到探测器焦平面上，所以从红外图像中得到的目标位置误差就是弹目视线相对于稳定平台的方位角和高低角[2]。而滚仰式半捷联位标器将探测器安置在弹体上，采用光学滑环结构实现视轴对前半球空间的任意指向[3]。来自目标的红外辐射需要经过特定的折线光路以后才能入射到探测器焦平面上，而且光路路径随着位标器框架的转动而变化[4-5]。所以红外图像中的目标位置误差不是直接反映了弹目视线相对稳定平台的方位角和高低角。本文基于光线反射定律和等距变换理论研究滚仰式光学滑环对目标的空间角位置测量，得到理论计算公式和近似计算公式，最后通过数值仿真验证了分析结果的正确性。

1 坐标系定义

红外成像位标器通过目标像在红外图像上形成的失调角来建立视线和位标器的空间位置关系。为了便于分析，先定义以下直角坐标系。

弹体坐标系-bbb。原点取为导弹质心。b轴和弹体纵轴重合，方向指向导弹头部。b轴位于弹体纵对称面内，和b轴垂直，向上为正。b轴和b轴与b轴成右手系。作为简化，以下分析时将弹体系根据需要进行平移。

外环坐标系-ooo。原点取为位标器回转中心。o轴和滚转框架转轴固连，方向指向导弹头部。-o轴位于过原点的o轴的垂面内，和俯仰框架转轴在该垂面的投影重合，方向沿弹径向外。o轴和o轴与o轴成右手系。

内环坐标系-iii。原点取为位标器回转中心。i轴和俯仰框架转轴固连，方向沿径向向外。i轴位于过原点的i轴的垂面内，且当内框架处于零位时，i轴落在俯仰轴和滚转轴确定的平面内，方向指向导弹头部。i轴和i轴与i轴成右手系。

根据坐标系的定义，假设框架结构安装理想，当滚转框架相对弹体转了s角，俯仰框架相对滚转框架转了s角时，各坐标系的变换关系如图1所示。

图1 各坐标系之间的变换关系

2 主要结构

滚仰式半捷联位标器的红外探测成像系统如图2所示。图中，b是焦平面中心，b-bbb是弹体系；是稳定平台回转中心，-ooo是外环系，-iii是内环系。焦平面阵列和弹体固连且垂直于弹轴。图2中平面镜1～4构成了光学滑环，其中平面镜1安置在稳定平台上，即和内环框架固连，镜面和内环系的轴平行，使得轴和轴均指向远离镜面的方向，且镜面和轴成45°角。平面镜2～4作为整体和外环框架固连。当内环框架无偏转时，平面镜2和平面镜1的镜面保持平行。平面镜3和平面镜2的镜面垂直相对放置，平面镜4和平面镜3的镜面平行相对放置。图2给出了光学滑环中的平面镜1～4随外环框架绕外环转轴相对于弹体转了s角，平面镜1相对于外环框架没有偏转的相对位置关系。

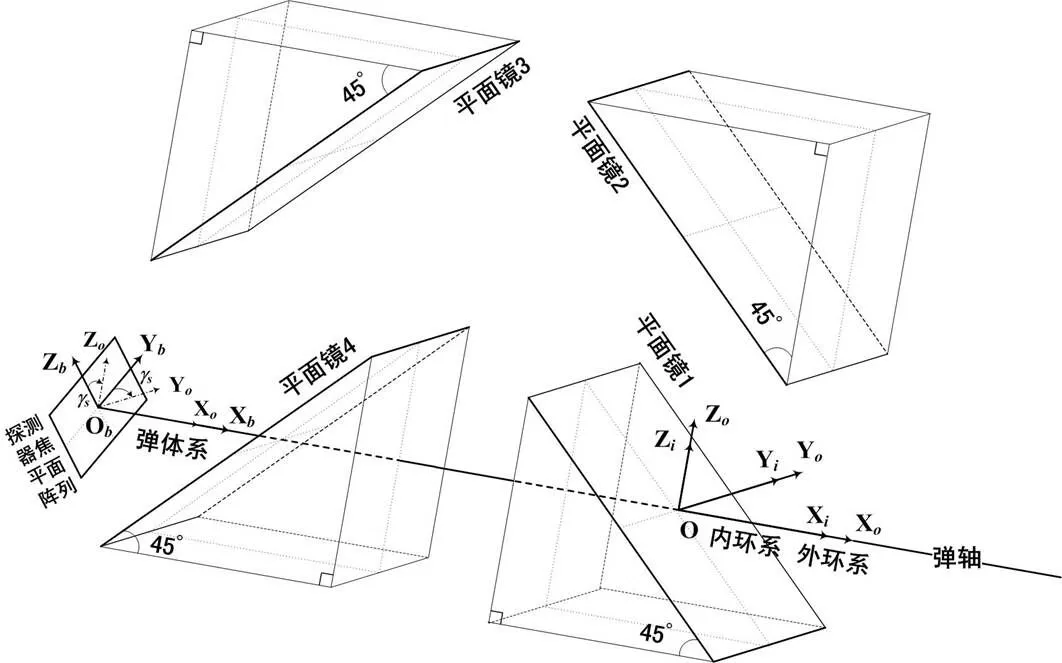
图2 滚仰式光滑环示意图

3 测角分析

目标进入视场中时，目标的红外辐射经过平面镜1反射到平面镜2上。根据光线反射定律，入射到平面镜2上的红外辐射等效于来自关于平面镜1对称位置处的像1所发出的红外辐射。同理，入射到平面镜3上的红外辐射等效于来自像1关于平面镜2对称位置处的像2所发出的红外辐射；入射到平面镜4上的红外辐射等效于来自像2关于平面镜3对称位置处的像3所发出的红外辐射；入射到探测器焦平面上的红外辐射等效于来自像3关于平面镜4对称位置处的像4所发出的红外辐射，如图3所示。

3.1 物象位置分析

将平面镜反射视为等距变换。四次平面镜反射分别记为等距变换，＝1, 2, 3, 4。记内环系为[;,,]，其中,,分别为内环系轴、轴、轴上的基矢。内环系经过等距变换1得到镜像系1:[1;1,1,1]；镜像系1经过等距变换2得到镜像系2：[2;2,2,2]；镜像系2经过等距变换3得到镜像系3：[3;3,3,3]；镜像系3经过等距变换4得到镜像系4：[4;4,4,4]。其中O表示镜像系的原点，,,分别为镜像系的轴、轴、轴上的基矢，＝1, 2, 3, 4。图4给出了外环框架角为s，内环框架角为s时各等距变换示意图。

3.1.1 等距变换1

由于平面镜1安置在稳定平台上，即和内环框架固连，所以不管内环框架偏转与否，在等距变换1的作用下，内环系的基矢和镜像系1的基矢之间保持唯一不变的对应关系。内环系的轴和镜面平行，轴和镜面成45°角，根据光线反射定律，有如下关系：

[1,1,1]＝[1(),1(),1()]＝[,,]1(1)

3.1.2 等距变换2

记内环框架没有偏转时，镜像系1为[1;1¢,1¢,1¢]。则当内环框架角为s时，相当于内环系绕轴转了s，对应[1;1¢,1¢,1¢]绕轴转－s。所以有：

根据光线反射定律，在等距变换2的作用下，有如下关系：

式中：。

Fig.3 Schematic diagram of reflect optical paths in the slick chain

图4 各等距变换示意图

Fig.4 Schematic diagram of equidistant alternating

由式(2)可得：

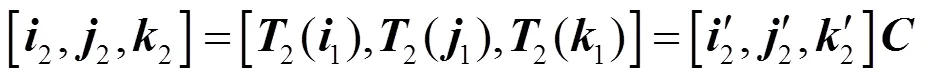
式(3)代入式(4)，再由式(2)可得：

3.1.3 等距变换3

根据光线反射定律，在等距变换3的作用下，有如下关系：

由式(4)可得：

式(6)代入式(7)，再由式(4)可得：

3.1.4 等距变换4

根据光线反射定律，在等距变换4的作用下，有如下关系：

由式(7)可得：

式(9)代入式(10)，再由式(7)可得：

3.1.5 变换的合成

目标经过光学滑环得到像4。将光学滑环的这种成像作用视为以上4个等距变换的合成，即＝4321。由式(1)、(5)、(8)、(11)可得光学滑环对内环系基矢的变换关系式：

记目标在光学滑环作用下所成的像为¢，即¢＝()。设在内环系中，＝[,,]，¢＝[¢,¢,¢]。由式(12)可得：

式中：()是的像在内环系中的坐标。

3.2 角度转换分析

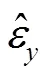
以为基点在视线上取单位矢量，其在内环系中的方位角为，高低角为，故在内环系中：

在光学滑环作用下，像¢＝()为连线¢¢上的单位矢量，由式(13)可得在内环系中：

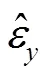
最后根据弹体系到内环系的坐标变换关系，可得视线相对于稳定平台的高低角和方位角为：

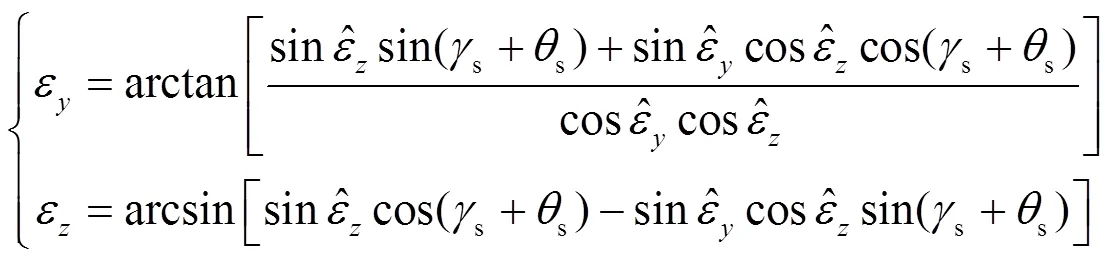
式(14)就是当外环框架角为s，内环框架角为s时，探测器的输出和视线相对稳定平台角位置的对应关系。该对应关系是可逆的，其逆关系为：

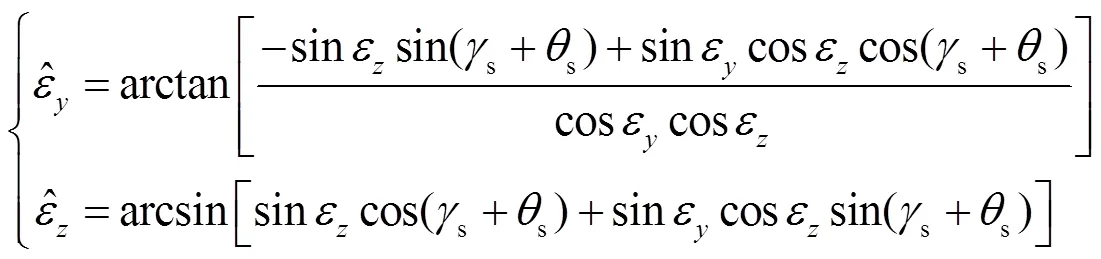
由于||≈0，||≈0，||≈0，||≈0，式(14)和式(15)的近似表达式为：

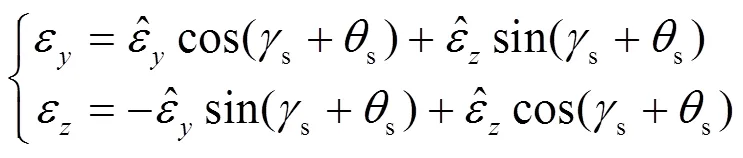
和

4 数值仿真

这里对从红外图像中得到的目标位置误差和视线相对稳定平台的实际角位置之间的对应关系进行数值仿真。

构造不同的视线相对平台的运动，仿真中设定视线相对稳定平台的运动学方程为：

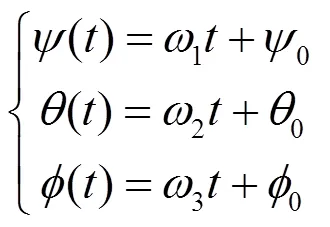
式中：1，2，3，0，0和0为某常值。通过弹目空间几何关系解算出视线相对稳定平台的方位角和高低角。仿真时间设为10s，采样时间间隔为0.01s。通过式(15)解算出目标像在探测器焦平面上的轨迹并和近似公式(17)的结果作比较。

取1＝100°/s，2＝－0.3°/s，3＝100°/s，0＝0，0＝1°，0＝0。这种情形表示视线相对于稳定平台的一般运动。图5给出了框架静止时目标像在焦平面上的轨迹，这里令外环框架角s＝80°，内环框架角s＝30°。图5中(a)、(b)和(c)给出了视线相对稳定平台的方位角和高低角，用像素数表示；(d)和(e)给出了仿真过程中框架角的变化曲线；(f)给出了探测器焦平面上目标像的轨迹，用像素数表示，圆点是轨迹起点，星号是轨迹终点，虚线圆圈所围的区域为视场。图6比较了用近似公式解算出的探测器的输出，(a)和(b)中黑色实线是精确解，红色虚线是近似解，(c)和(d)是近似误差曲线，用像素数表示。

图7给出了框架运动时目标像在焦平面上的轨迹。这里设定框架的相对运动方程为：

取1＝2＝0.025Hz，1＝2＝0。

图7中(a)、(b)和(c)给出了视线相对稳定平台的方位角和高低角，用像素数表示；(d)和(e)给出了仿真过程中框架角的变化曲线；(f)给出了探测器焦平面上目标像的轨迹，用像素数表示，圆点是轨迹起点，星号是轨迹终点，虚线圆圈所围的区域为视场。图8比较了用近似公式解算出的探测器的输出，(a)和(b)中黑色实线是精确解，红色虚线是近似解，(c)和(d)是近似误差曲线，用像素数表示。

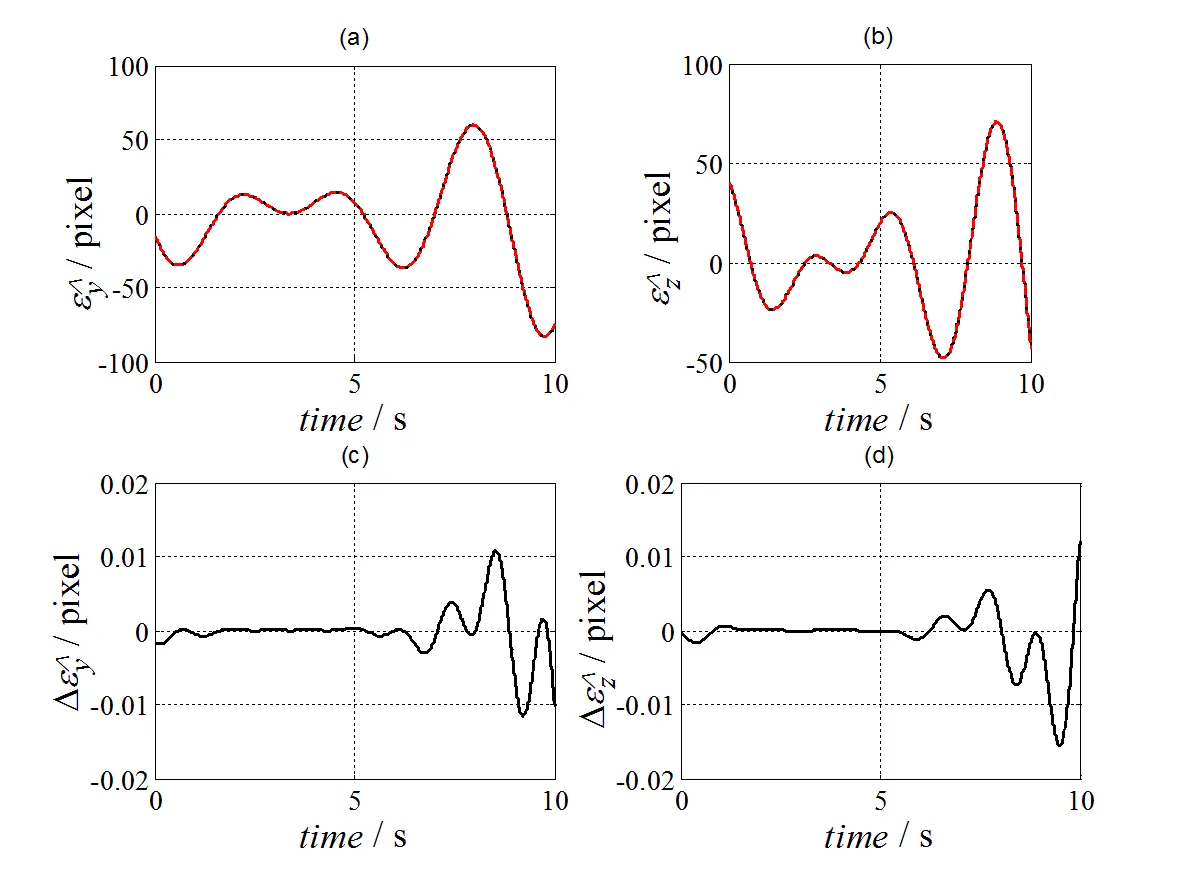
图6 近似公式解算出的探测器输出及近似误差

图7 视线相对平台的运动、框架的运动及目标像在探测器焦平面上的轨迹

图8 近似公式解算出的探测器输出及近似误差

5 结论

本文研究了滚仰式光学滑环关于视线相对于稳定平台的角位置计算。基于光线反射定律和等距变换理论，分析并给出了从红外图像中得到的目标位置误差和视线相对平台的角位置之间的转换关系式及近似公式，并对所得结果进行了数值仿真。仿真结果表明，近似公式的精度（小于0.05个像素）满足工程使用要求。

[1] 花文涛, 刘凯, 丁海山. 滚仰式红外导引头视线角速率提取方法研究[J]. 红外技术, 2015, 37(1): 63-66, 72.

Hua Wentao, Liu Kai, Ding Haishan. Research on roll-pitch infrared seeker LOS rate extraction[J]., 2015, 37(1): 63-66, 72.

[2] 薛丹. 光电稳定平台框架结构探讨[J]. 光机电信息, 2011, 28(3): 33-36.

Xue Dan. Study on Multi-structures of Gimbals for Electro-optical Reconnaissance Platform[J]., 2011, 28(3): 33-36.

[3] Rudin,R.T.. Strapdown stabilization for imaging seekers. AIAA, A93-42219, 1993.

[4] 王军平, 尚超, 吴军彪. 四元数法在光滑环系统坐标变换中的应用研究[J]. 航空兵器, 2011(3): 24-27.

Wang Junping, Shang Chao, Wu Junbiao. Application of Quaternion Method in Coordinate Conversion of Slick Chain System[J]., 2011(3): 24-27.

[5] 尚超, 王军平, 吴军彪. 滚仰式光滑环物像变换关系仿真研究[J]. 红外与激光工程, 2011, 40(9): 1768-1773.

Shang Chao,Wang Junping,Wu Junbiao. Simulation of object-image transformation for roll-pitch seeker with slick chain[J]., 2011, 40(9): 1768-1773.

Analysis on Measurement for Angular Positionof Slip Chain in Roll-pitch Seeker

HU Heng-song1，DING Hai-shan1，HUA Wen-tao1，ZHAO Gui-jin1, 2

(1.,471009,;2.,471009,)

Roll-pitch seeker with slip chain is widely used in miniature seekers. Because of introducing reflective optical paths, the measurement for the angular position of the target in the space is more complicated than traditional imaging tracking systems. Based on the law of reflection and equidistant alternating theory, roll-pitch seeker with slip chain is studied to measure the angular position of the target in the space. The theoretical calculation formula and the approximate formula are obtained. At last, the analysis results are tested by numerical simulations.

slick chain，roll-pitch，angular position in the space，equidistant alternating，stable platform

TP765.3

A

1001-8891(2015)10-0883-07

2015-04-29；

2015-05-28.

胡恒松（1982-），男，工程师，主要研究方向为稳定平台式红外目标位标器总体设计、位标器试验技术、惯性器件应用研究等。

航空科学基金项目，编号：20120112006。