小面积、微功耗增量型Sigma-Delta ADC设计

姚立斌，陈 楠，韩庆林



小面积、微功耗增量型Sigma-Delta ADC设计

姚立斌，陈 楠，韩庆林

（昆明物理研究所，云南 昆明 650223）

模拟数字转换器（ADC）是智能化传感器的一个重要组成部分。阵列型传感器应用对ADC的功耗及芯片面积都具有较高的要求，同时传感器本身特性要求ADC具有较高的精度，对阵列型传感器用ADC的设计提出了挑战。在分析各类型ADC的性能优劣势的基础上，提出了应用增量型Sigma-Delta ADC来设计阵列型传感器应用。介绍了增量型Sigma-Delta ADC的架构设计以及电路设计，并在0.18mm CMOS工艺下流片。在40kS/s的转换速度下，所设计的ADC达到了15bit的精度，功耗为58mW，单个ADC的芯片面积为10mm×530mm。测试结果表明增量型Sigma-Delta ADC非常适合于阵列型传感器应用。

模-数字转换器（ADC）；增量型Sigma-Delta ADC；微功耗电路设计

0 引言

随着半导体工艺技术的不断发展，各类半导体传感器以及微机械系统传感器得到广泛应用。在各传感器节点就将传感器信号数字化是基本需求，因而需要在传感器上集成高性能的模拟-数字转换器（ADC）来完成传感器输出的模拟信号的量化。在传感器应用中，ADC的精度往往要求较高；同时，在手持设备及传感器节点应用中，ADC的功耗是首先要考虑的指标。其次，传感器应用的特点往往需要大量的传感器形成阵列，例如图像传感器、指纹传感器及各种生物医学传感器等。在此类应用中，芯片面积往往受到限制。因此，在数字化的阵列型传感器中，ADC是设计的关键和难点[1-2]。

针对传感器应用要求，需要对ADC进行设计优化。ADC的分辨率、转换速度、功耗及芯片面积是通常ADC应用关注的指标。对于传感器应用，通常要求ADC具有较高的分辨率，例如多数物理量测量传感器要求14位以上的分辨率。ADC的转换速度则依应用的不同可达到数十kS/s之间。对于阵列型传感器应用，ADC的面积受阵列尺寸限制，对设计和版图实现带来困难[3]。

本文依据阵列型传感器应用对ADC的需求，设计了一个二阶增量型Sigma-Delta ADC，在ADC精度、功耗及版图面积之间折中设计。从ADC架构选型，到系统设计、单元电路设计、仿真及版图设计都作了详细介绍，最后给出了测试结果。

1 增量型Sigma-Delta ADC

图1给出了各种不同架构的ADC的速度和分辨率的关系。总体来说，ADC的分辨率与转换速度是一对矛盾。对于传感器应用来说，需要相对较高的分辨率及较低的速度，因而积分型（Integrating）ADC和过采样ADC较为适合传感器应用。

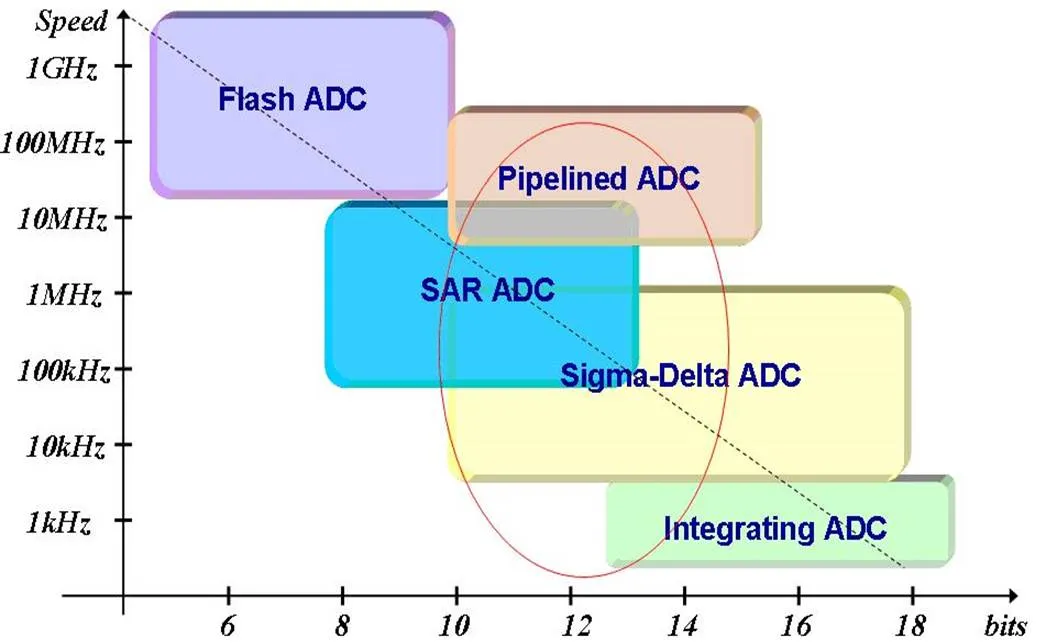
图1 ADC的速度与分辨率关系

基于过采样技术的Sigma-Delta ADC可以实现高精度的模拟-数字转换。其基本原理为采用过采样技术将量化噪声分散在采样频带内，再通过数字滤波器滤除信号频带外的噪声，从而达到降低量化噪声，提高分辨率的目的。

单独采用过采样技术来提高ADC的分辨率效果有限。在过采样技术的基础上，Sigma-Delta ADC增加噪声整形技术，将量化噪声推到高频带，进一步减小了信号带宽内的噪声，提高信噪比。噪声整形技术如图2所示，B为信号频带，为量化噪声功率，3根曲线分别为单纯过采样、一阶Sigma-Delta调制器及二阶Sigma-Delta调制器的量化噪声频谱分布图。Sigma-Delta ADC在过采样技术的基础上，增加了噪声整形技术，由Sigma-Delta调制器实现。Sigma-Delta调制器对于输入信号来说是一个低通滤波器，在信号频带B内输入信号不受衰减；但对于量化噪声来说，Sigma-Delta调制器是一个高通滤波器，阻止了量化噪声进入信号频带B内。由图中可以看出，经过抽取滤波器后，进入信号频带B内的量化噪声功率是不同的。Sigma-Delta调制器阶数越高，进入信号频带B内的量化噪声功率越小，ADC的分辨率就越高。

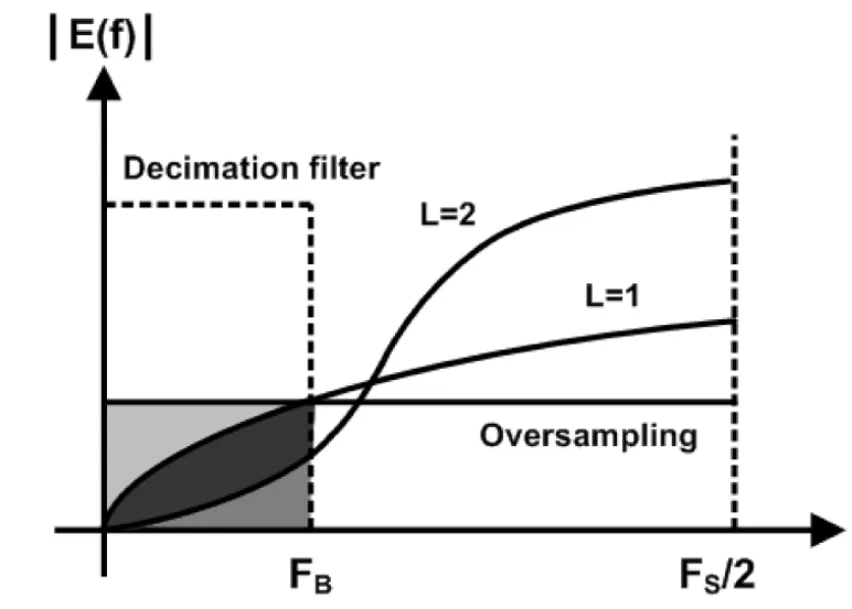
图2 噪声整形原理示意图

不同于其他类型的ADC，由于采用了过采样技术及噪声整形技术，Sigma-Delta ADC可以以较低位数的量化器来实现高分辨率的量化。例如可以采用天然线性的单比特量化器，即比较器来实现量化，不但简化了电路，并且可以保证线性度。因而Sigma-Delta ADC对模拟电路中失配、失调等误差不敏感，无需外加校正等手段即可实现较高的转换精度。通过设计不同的过采样率及Sigma-Delta调制器阶数，Sigma-Delta ADC可以实现非常高的精度。目前已有24bit分辨率的Sigma-Delta ADC产品。

传统Sigma-delta ADC适用于对连续时间信号进行持续采样，数字抽取滤波器连续工作。因而其数字抽取滤波器较为复杂，不但设计困难，且消耗大量的芯片面积及功耗，不适合面积受限的阵列型ADC应用。

增量型Sigma-Delta ADC[4]（Incremental Sigma- Delta ADC）可以看作是Sigma-Delta ADC的一个改进。它将Sigma-Delta调制器及数字抽取滤波器每个采样周期复位1次，这样可以用简单的累加器来实现数字抽取滤波器，以此简化数字抽取滤波器的设计，其功耗及版图面积等均大大降低。在阵列型传感器应用中，需要对多个传感器输出信号进行多路切换，因而切换后的传感器输出信号是时间离散信号，即在ADC的每个采样周期内输入信号是不变的，且不同采样间彼此独立。因此可以在阵列型传感器应用中采用增量型Sigma-Delta ADC。

作为Sigma-Delta ADC的一种改进，增量型Sigma- Delta ADC遗传了Sigma-Delta ADC的大部分特点，如天然的高线性度、对电路失配的高容限、分辨率与速度互换等。同时，增量型Sigma-Delta ADC有其自身的特点，如简单的数字抽取滤波器设计[5-6]。对于增量型Sigma-Delta ADC的数字抽取滤波器设计，除了经典的累加器设计外，文献[7]给出了一种新思路的优化设计，能够进一步简化数字抽取滤波器设计，并介绍了详细的设计方法。

增量型Sigma-Delta ADC还具有一个特性，其变换精度与变换速度在一定范围内可以互相交换。对于给定的ADC分辨率，每次变换需要的时钟周期数是一定的。将给定ADC分辨率降低，则每次变换需要的时钟周期数将降低。这样的特性可以实现可变分辨率ADC[8]，在高分辨率模式下，ADC速度降低；在高速模式下，ADC分辨率降低。

2 增量型Sigma-Delta ADC电路实现

对于阵列型传感器应用，将会有大量相同的电路在芯片上实现，电路设计的首要问题是功耗及芯片面积。增量型Sigma-Delta ADC指标为：分辨率15bit，转换速度40kS/s，功耗小于100mW，版图面积一维方向限制在10mm，另一方向尽量小。增量型Sigma-Delta ADC从结构上解决了精度的问题，功耗及版图面积的问题需要针对特定应用的需求，重点在电路设计层面来解决。

2.1 增量型Sigma-Delta ADC系统架构选择

上述ADC指标对电路设计带来巨大的挑战。首先，要在10mm的版图宽度内实现整个ADC的版图设计，必须要求ADC的电路尽量的简洁。其次，功耗的限制要求电路设计必须尽可能的采用效率较高的电路架构。再加上15bit的相对较高的精度要求，ADC的架构选取成为一个关键问题。

对于一阶增量型Sigma-Delta ADC来说，其数字抽取滤波器可以由简单的计数器构成，可以大大简化电路设计。但一阶Sigma-Delta ADC存在1个缺点，对于bit的ADC分辨率，需要2个时钟周期才能实现1次变换[9]。对于40kS/s的变换速度及15bit的分辨率，需要ADC时钟频率高达131MHz。如此高频率的时钟信号在整个ADC阵列上分配将消耗大量功率，＜100mW的功耗指标无法达成，因而必须采用更有效率的方案。

由图2可以看出，增加Sigma-Delta调制器的阶数可以增强噪声整形的能力。为降低所需时钟频率，可以采用二阶增量型Sigma-Delta ADC，如图3所示。整个增量型Sigma-Delta ADC由二阶Sigma-Delta调制器及数字抽取滤波器构成。由于采用了更有效的噪声整形技术，bit的二阶增量型Sigma-Delta ADC需要大约2(N＋1)/2个时钟周期就能实现一次变换[8]。对于40kS/s的变换速度及15bit的分辨率，需要ADC时钟频率大约为10MHz。相对于一阶增量型Sigma- Delta ADC，这是一个巨大的进步。

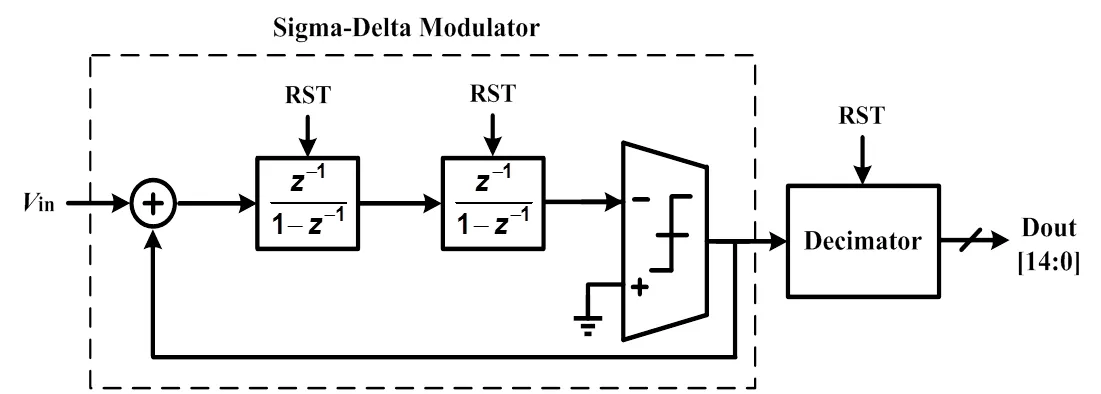
图3 二阶增量型Sigma-Delta ADC系统图

2.2 Sigma-Delta调制器电路设计

二阶增量型Sigma-Delta调制器的电路图如图4所示，Sigma-Delta调制器由两级积分器及量化器组成，电路采用开关电容电路实现。为减小版图面积，电路采用单端形式，对电源纹波及干扰的抑制上有所折中。

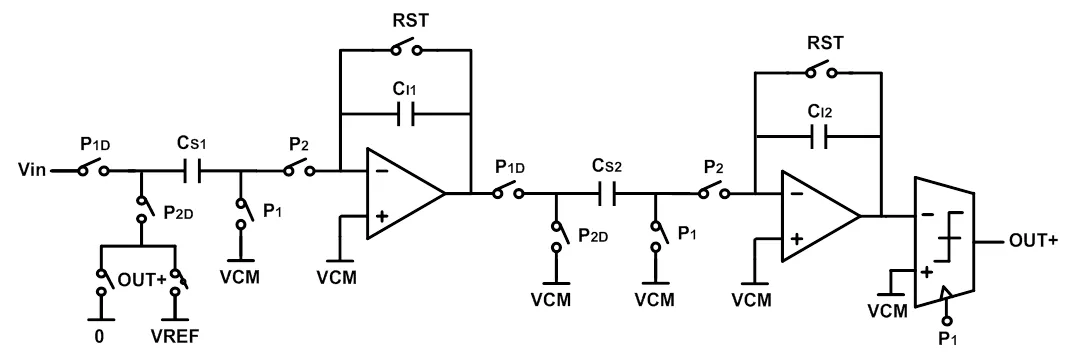
图4 二阶增量型Sigma-Delta调制器电路图

Sigma-Delta调制器电路中主要部分为放大器，如图5所示。为提高电源效率，采用单级放大器架构，同时输出晶体管采用AB类偏置，保证具有较高的驱动电流。将放大器的增益带宽积设计为大约5倍的时钟频率，以保证开关电容电路的建立精度。对于增量型Sigma-Delta ADC来说，放大器的增益对ADC的线性度的影响有限，因而简单的单级放大器架构能够满足系统的要求。

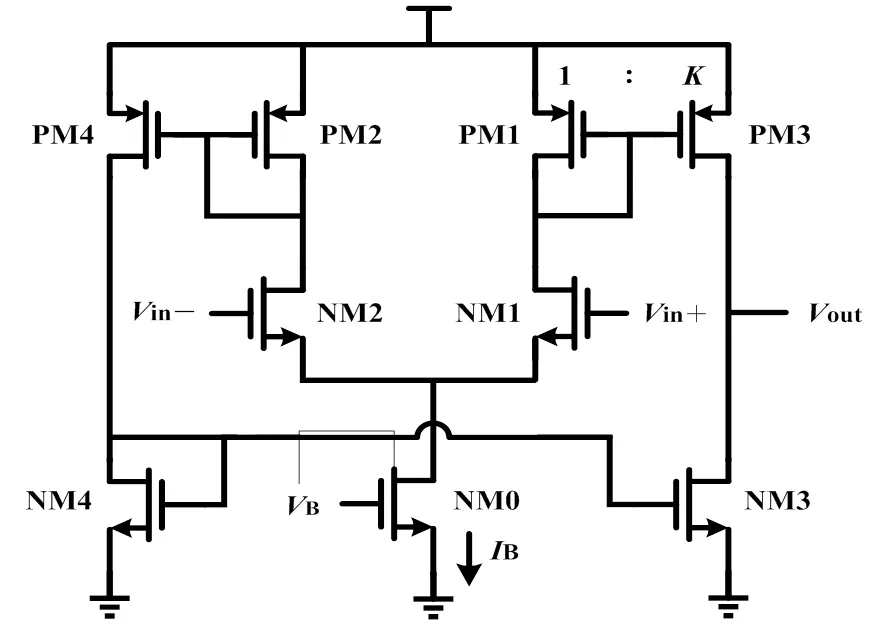
图5 放大器电路图

单比特量化器采用简单的比较器来实现，其电路图见图6。因Sigma-Delta ADC对量化器的输入失调电压容限较高，同时为了简化电路及降低功耗，采用动态比较器电路。电路仅在时钟信号的上升沿产生功耗，其它时间不消耗功率。

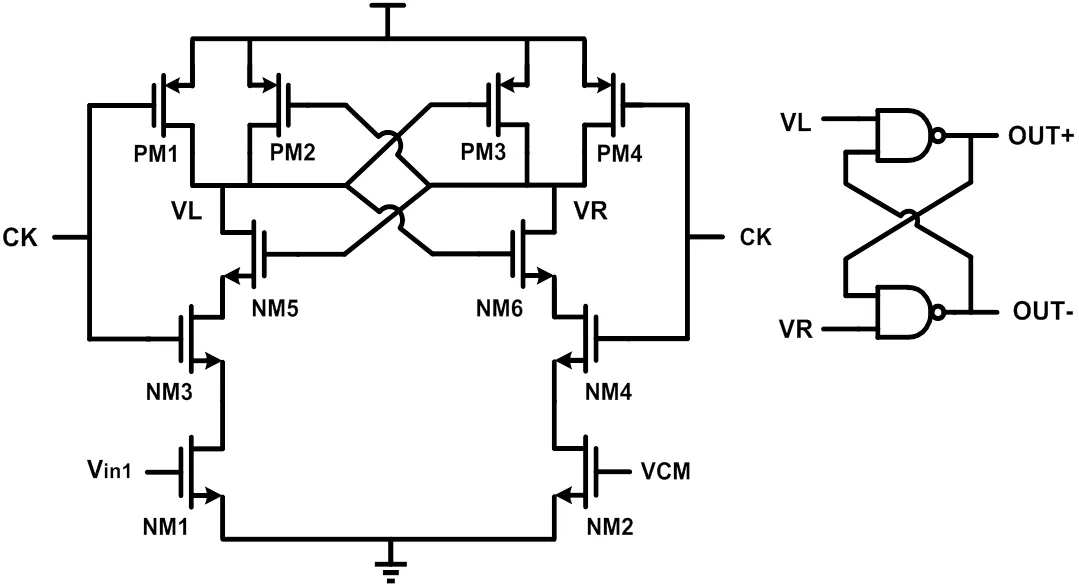
图6 比较器电路图

Fig. 6 Schematic of the comparator

2.3 数字抽取滤波器及时钟产生电路

数字抽取滤波器的原理框图如图7所示。Sigma-Delta调制器输出的一位比特流首先进入8位的计数器计数，计数得到的8位数据再累加，最后得到15位的输出字[9]。为进一步降低功耗，计数器采用动态D触发器构成。累加器采用静态逻辑电路实现。因版图尺寸的限制，数字电路全部采用手动布局布线。

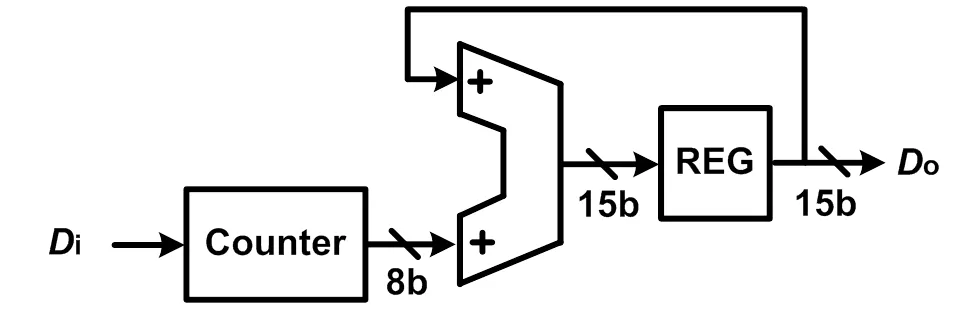
图7 二阶增量型Sigma-Delta调制器电路图

开关电容电路需要两相非交叠时钟信号来驱动开关，其电路如图8所示。电路采用交叉反馈实现非交叠的时钟，其中一路带延时关断以减少开关的电荷注入效应。对于阵列应用来说，因版图面积较大，需要多个时钟产生电路来产生本地时钟驱动信号，避免两相时钟的长距离传输导致的交叠。

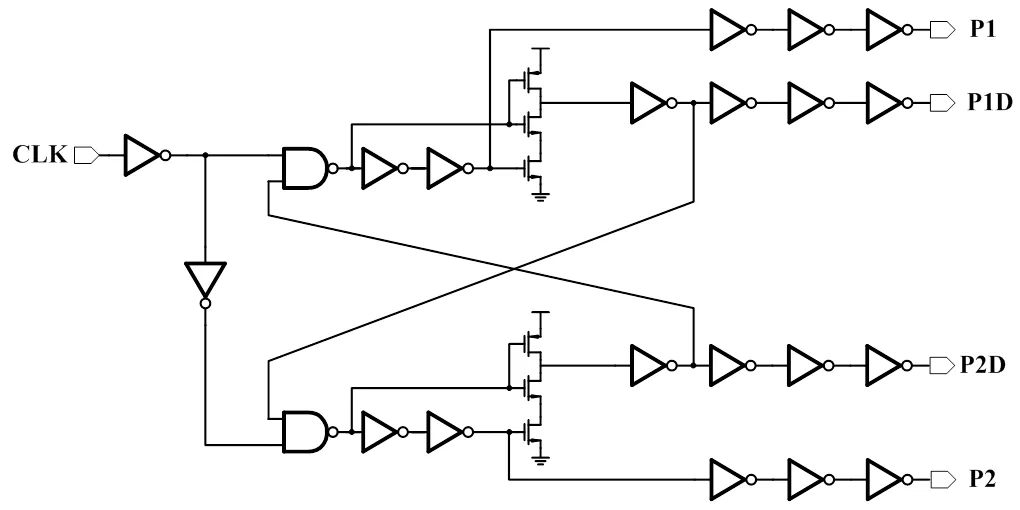
图8 时钟产生电路图

3 测试结果

设计的二阶增量型Sigma-Delta ADC采用0.18μm CMOS工艺制备，芯片显微照片见图9，为4个ADC的阵列，单个ADC的芯片面积为10mm×530mm。芯片粘接安装在专门设计的PCB板上进行测试。Sigma-Delta 调制器等模拟部分电源电压为1.8V，模拟部分功耗为48mW，数字部分电源电压为1.2V，功耗为10mW，整个增量型Sigma-Delta ADC的总功耗为58mW。

图9 二阶增量型Sigma-Delta ADC芯片照片

图10所示为测试的二阶增量型Sigma-Delta ADC输入输出曲线。可以看出在1.5V的输入范围内ADC的线性良好。图11所示为测试的二阶增量型Sigma-Delta ADC差分非线性曲线。在整个输入范围内，ADC的差分非线性度都小于1个LSB。

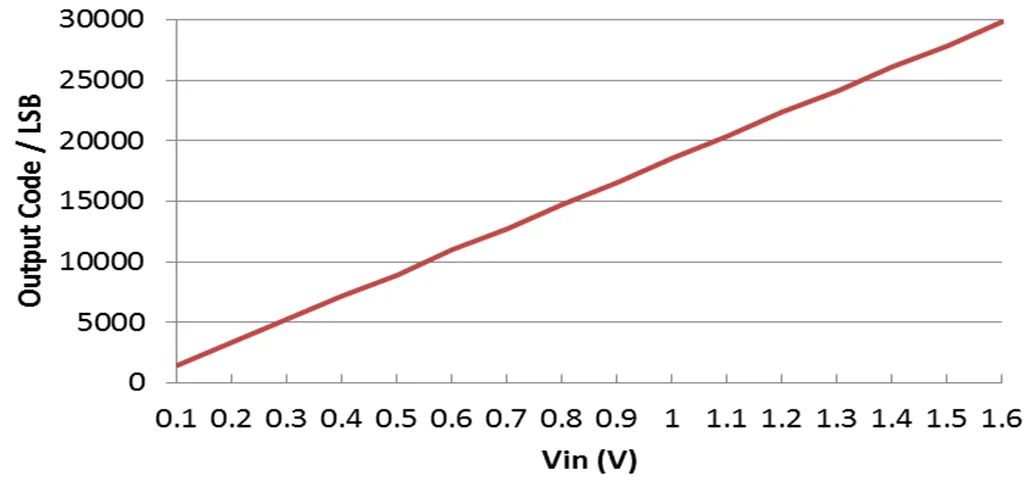
图10 二阶增量型Sigma-Delta输入输出特性曲线

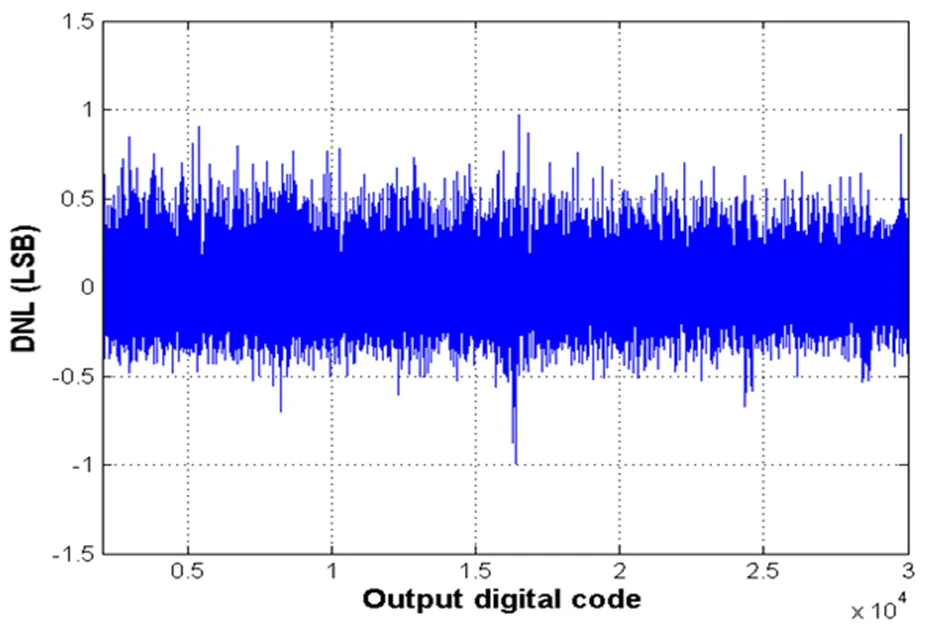
图11 二阶增量型Sigma-Delta ADC差分非线性测试结果

图12所示为测试的二阶增量型Sigma-Delta ADC积分非线性曲线。在整个输入范围内，ADC的积分非线性度为±30个LSB。ADC积分非线性性能不佳的主要原因是有限的放大器直流增益导致的积分器泄漏。通过设计高增益的放大器有利于降低ADC的积分非线性，但代价是更大的版图面积及更高的功耗。对于特定的传感器应用来说，这样的积分非线性是可以接受的。

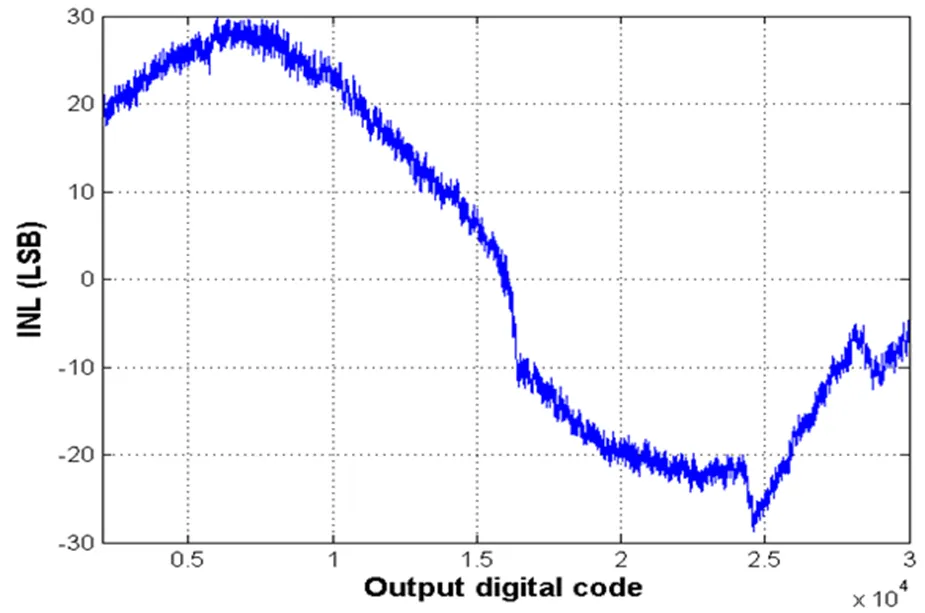
图12 二阶增量型Sigma-Delta ADC积分非线性测试结果

图13所示为测试的二阶增量型Sigma-Delta ADC在不同的输入直流电压下的输出噪声。测试结果表明在全输入范围内此ADC的输出噪声大约为1～1.6 LSB。此噪声测试结果包含了输入的直流信号的噪声，ADC本身的噪声小于这个测试结果。

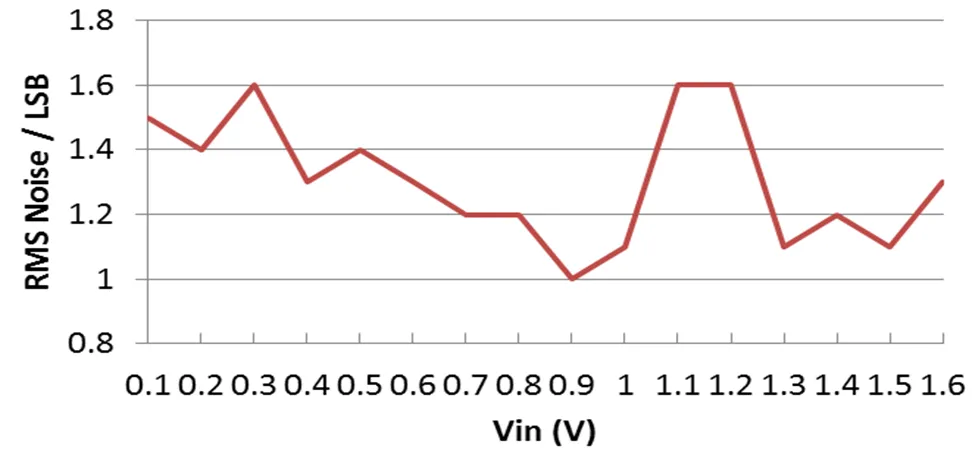
图13 二阶增量型Sigma-Delta ADC噪声测试结果

综合分析测试结果，可以看出通过优化设计二阶增量型Sigma-Delta ADC，可以达到电路精度、功耗、面积的折中。针对不同的应用需求，可以通过ADC架构及电路的优化设计，来突出某一参数或取得整体性能的提升。

4 结论

增量型Sigma-Delta ADC因为其本身电路的简洁，易达到小芯片面积及低功耗的设计目标。同时，其过采样特性对模拟电路的非理想特性容限较高，能达到较高的变换精度。对于阵列型智能化传感器应用来说，增量型Sigma-Delta ADC是一个较好的架构。本文所设计的增量型Sigma-Delta ADC在0.18mm CMOS工艺下实现，在非常有限的版图面积内实现了整个ADC，同时整个ADC的精度及功耗指标都非常具有竞争力。由于积分器泄漏的原因导致ADC的积分非线性特性不佳，可以通过更有效的电路设计来加以弥补，代价是更大的电路功耗及芯片面积。测试结果表明本文介绍的二阶增量型Sigma-Delta ADC非常适合于功耗、面积受限的阵列型传感器应用。

[1] 陈楠, 姚立斌. 阵列型图像传感器模数转换技术[J]. 红外技术, 2014, 36(10): 769-776.

CHEN Nan, YAO Li-bin. Analog to digital conversion techniques in array image sensors[J]., 2014, 36(10): 769-776.

[2] Zhong S Y, Yao L B. A low-power small-area ADC Array for IRFPA Readout[C]//,,2013, 8907: 89075G.

[3] Shin M S, Kim J B, Kim M K, et al. A 1.92-Megapixel CMOS image sensor with column-parallel low-power and area-effcient SA-ADCs[J]., 2012, 59: 1693-1700.

[4] Robert J, Deval P. A second-order high-resolution incremental A/D converter with offset and charge injection compensation[J]., 1988, 23: 736-741.

[5] Jansson C. A high-resolution, compact, and low power ADC suitable for array implementation in standard CMOS[J]., 1995, 42(11): 904-912.

[6] Markus J, Silva J, Temes G C. Theory and applications of incremental ΔΣ converters[J]., 2004, 51(4): 678-690.

[7] Kavusi S, Kakavand H, Abbas El Gamal. On incremental Sigma-Delta modulation with optimal filtering[J]., 2006, 53(5): 1004-1015.

[8] Liang J, Johns D A. A frequency-scalable 15-bit incremental ADC for low power sensor applications[C]//(),, 2010: 2418-2421.

[9] Chae Y, Cheon J, Lim S. A 2.1 M pixels, 120 frame/s CMOS image sensor with column-parallel ΔΣ ADC architecture[J]., 2011, 46(1): 236-247.

Compact, Micro-power Incremental Sigma-Delta ADC Design

YAO Li-bin，CHEN Nan，HAN Qing-lin

(,650223,)

The analog-to-digital converter (ADC) plays an important role in array sensor applications. This kind of applications imposes very stringent power and chip area restriction to the ADC. On the other hand, the sensor itself requires high-resolution of the ADC. All these requirements place challenge to the ADC design. By carefully study of the ADC topology, the incremental Sigma-Delta ADC is proposed as it produces better resolution, power and chip area trade-off. The topology and the circuit design of the proposed incremental Sigma-Delta ADC are introduced in details. Implemented in a 0.18mm CMOS technology, the proposed ADC consumes 58mW power consumption at the conversion speed of 40kS/s and produces 15bit digital output. The chip area of one single ADC is 10mm×530mm. The measurement result proves the proposed incremental Sigma-Delta ADC is suitable for array sensor applications.

analog-to-digital converter (ADC)，incremental Sigma-Delta ADC，low-power design

TN386

A

1001-8891(2015)12-1011-05

2015-11-20；

2015-12-05.

姚立斌（1968-），男，博士，研究员，博士研究生导师，主要研究方向为混合信号集成电路设计。

云南省科技厅应用基础研究计划重大项目，编号：2013FC009。