水下自动武器后坐能量测试传感器的结构优化设计
2015-04-01王丽丽余红英
王丽丽,余红英,杨 臻,李 萍
(1.中北大学 计算机与控制工程学院,山西 太原030051;2.中北大学 机电工程学院,山西 太原030051)
0 引 言
水下武器在研制过程中由于其特殊的使用环境,武器的测试方法与常规的地面武器有较大的差异[1,2]。自动机作为自动武器的心脏部件,其后坐能量的大小是衡量武器性能的重要指标之一[3]。已有的自动机后坐能量测试方法是将武器安装在固定滑台上,通过测量武器发射时的后坐速度间接测试后坐能量[4,5],后坐速度利用磁电式传感器间接测量得到[6]。
目前采用的磁电式传感器一般选用高导磁的金属材料作为铁芯,虽提高了灵敏度,但如果选用的材料能形成回路,将会在铁芯表面形成涡流,产生感应电动势,阻止速度线圈中的总感应电动势随磁铁速度的改变而产生的变化,严重降低传感器的灵敏度和动态特性[7,8]。因此,需对该传感器进行优化设计,使其在保证高灵敏度的同时,减小甚至消除涡流带来的影响[9]。
本文提出了一种基于电磁感应原理的测速传感器的结构优化设计,试验表明:该设计结构动态性能更好,更能精确反映自动机的运动规律。
1 传感器的结构优化设计
1.1 传感器本体结构优化
本文提出的对磁电式传感器的优化设计主要是以环氧树脂板代替铁芯。环氧树脂板具有良好的力学性能,可以适应各种应用对形式提出的要求,并且绝缘,避免了在自动机测量中涡流等对传感器灵敏度产生的影响。本文根据自动机的行程选择合适长度的矩形柱形的环氧树脂板作为线圈的铁芯。在环氧树脂板上用漆包线紧密缠绕一层线圈作为速度线圈,在速度线圈表面利用丝包线等间距正反多圈间绕而成位移线圈。由于环氧树脂板不导磁,为保证传感器的灵敏度,铁芯需具有较高的导磁率,故在速度线圈与环氧树脂板之间加一层坡莫合金片。该合金由铁镍两种元素组成,选择铁镍比例合适的合金,能够使其在弱磁场下具有极高导磁率。内部结构如图1 所示。

图1 传感器内部结构图Fig 1 Inner structure of sensor
1.2 传感器工作原理
测量时,永久磁铁与连接件组合成磁头件,与被测件刚性连接。如图2 所示,当自动机工作时,磁头件随着自动机的运动而运动,永久磁铁将在速度线圈内产生如图2 所示的磁场,并且磁通量Φ 的大小随着永久磁铁与速度线圈的距离按指数衰减。当被测件以速度v 运动时,将带动永久磁铁在速度线圈表面运动,使穿过各匝速度线圈的磁通量随着各匝线圈与永久磁铁的距离而产生变化,即各匝速度线圈中的磁场强度也是x 的函数B=B(x)。设速度线圈的横截面积为S,则通过各匝速度线圈的磁通量
当线圈几何参数一定时,S 是常量,所以,有

对式(2)进行变换
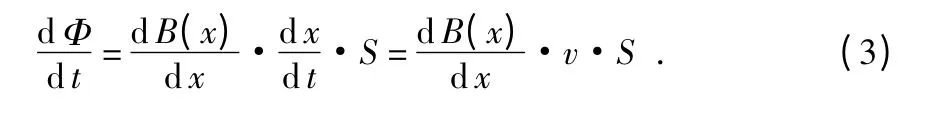
因此,由法拉第电磁感应原理


图2 工作原理Fig 2 Operating principle
由式(4)可以看出,在各匝速度线圈中将产生与速度v呈正比的感应电动势,而总的感应电动势应为各匝感应电动势之和。上述公式中x 轴方向表示速度线圈轴向方向,N 为速度线圈匝数。
永久磁铁在运动时,同时也从位移线圈表面滑过,经过一个绕组产生一个电动势信号。由于位移线圈中两个相邻绕组的绕向相反,对外电路来说,相邻绕组中产生方向相反的感应电动势,故产生的位移信号为锯齿波,相邻的峰尖和峰谷对应的时间间隔相当于永久磁铁通过一个节距所用的时间,通过计算产生锯齿波的个数即可得到自动机运动的位移。
1.3 信号调理单元优化
自动机运动剧烈,在对自动武器进行测量时,往往是多个参数同时测量,使用磁电式传感器测出的信号通常比较微弱,多种因素的干扰会对自动机的信号产生影响,故本文设计了信号调理电路对自动机输出的信号做进一步的处理,使其能更直观准确地反映自动机的运动规律。信号调理电路如图3 所示。

图3 信号调理电路Fig 3 Signal conditioning circuit
2 测试结果
利用封装好的传感器,在某自动武器动态参量测试基地进行了多次后坐能量测试,图4 所示为速度—时间曲线,图5 所示为位移—时间曲线。
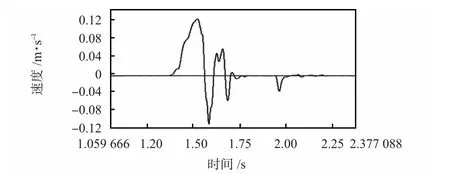
图4 速度—时间曲线Fig 4 v-t curve
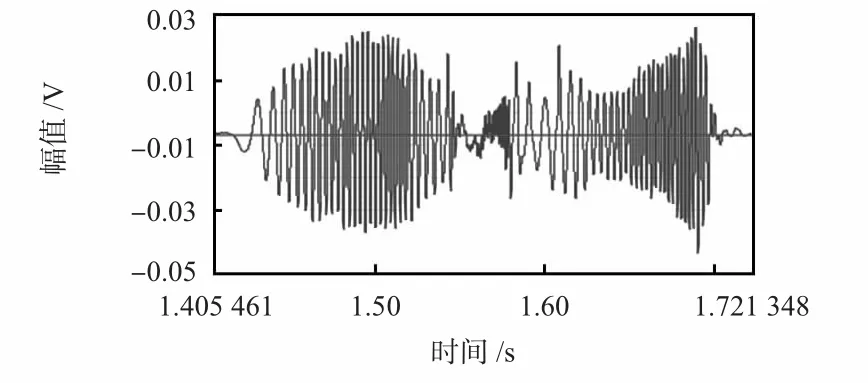
图5 位移—时间曲线Fig 5 s-t curve
炮弹射击时,火药压力产生的冲量向前发射弹头,向后使武器后坐,经过一段时间,气体作用结束,自动机速度下降,但是由于惯性继续后坐,后坐到位后,在复进簧伸张力的作用下复进,经过一段时间复进到位,开始第二发炮弹的射击。在复进到位时,由于撞击等原因,又会反方向运动一小段距离。在软件中对位移信号进行巴斯沃特滤波处理,并经过相关积分算法处理后的位移—时间曲线如图6 所示。

图6 滤波处理后的位移—时间曲线Fig 6 s-t curve after filtering
3 数据分析
为了验证本传感器的精确度与灵敏度,对传感器的测量结果进行了误差分析与不确定度分析。
3.1 误差分析
本传感器多次测量的数据如表1 所示。

表1 传感器测量数据Tab 1 Sensor measurement data
算术平均值为


表2 残余误差Tab 2 Residual error
根据残余误差代数和校核规则,已知n=9,经计算

其中,σ 为算术平均值的标准差,算术平均值的极限误差按τ 分布计算,取α=0.05,查表得到:τα=2.31,极限误差为

最后测量结果通常用算术平均值及其极限误差来表示,即
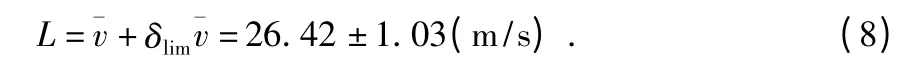
根据有关资料可知,传感器的测量精确度满足要求。
3.2 不确定度分析
根据分析,不确定度采用B 类评定方法[10],有以下几个方面:
1)采集卡满幅量程为5 V,16 位,相对误差为
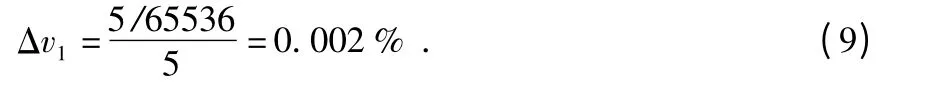
2)采样频率100 kHz,相对误差为

3)传感器自身灵敏度,相对误差公式为

当温度变化时,由铜线本身的属性可得
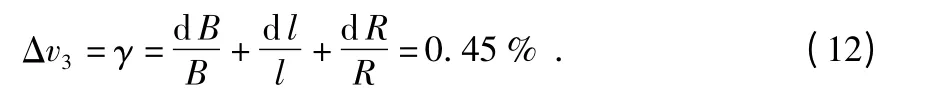
4)永久磁铁的磁性会随温度和时间的推移而变化,在受到冲击或振动作用后,磁感应强度会有些损失,约下降1%,故

μ1=0.00067%,μ2=0.42%,μ3=0.15%,μ4=0.33%.
因各个不确定度分量相互独立,合成不确定度为

因各个不确定度分量和合成标准不确定度皆基于误差范围为3σ,故取包含因子k=3,则系统不确定度为

经过查询有关资料[4],优化后的传感器结果的不确定度优于已有的水下测试传感器,传感器的灵敏度得到了很大的提高。
4 结 论
本文提出的优化方法有效地解决了水下自动机运动参数测量中传统传感器金属铁芯产生的涡流影响传感器精度的问题,测试信号经处理单元后,能准确地反映出自动机的运动规律。通过对测量数据的分析,传感器的精确度和灵敏度都得到了提高。在测试的过程中,不仅单发测试结果准确,连发射击测试结果也客观可靠,对自动武器的水下工作的研究提供了有力的帮助。
[1] 吴祥海,樊丽霞,石小晶,等.漫谈自动武器测试技术[J].测试技术学报,1997,11(3):35-42.
[2] 王 蕾.基于虚拟仪器的自动机运动规律研究[D].南京:南京理工大学,2007.
[3] 张永德.枪械后坐能量测试方法研究[J].华北工学院学报,2005,26(3):219-221.
[4] 狄长安,孔德仁,王昌明,等.水下发射装置后坐能量测试及特性分析[J].火炮发射与控制学报,2006(3):47-50.
[5] 陈 静,王昌明.水下枪械自动机速度测量系统[J].传感器与微系统,2006,25(1):66-68.
[6] 徐科军.传感器与检测技术[M].北京:电子工业出版社,2010.
[7] 吴祥海.YSW 型永磁式速度位移传感器[C]∥全国传感器及其应用学术讨论会论文集,武汉,1984:351-356.
[8] 孔德仁.兵器动态参量测试技术[M].北京:北京理工大学出版社,2013.
[9] Yu Y,Yang T,Du P.A new eddy current displacement measuring instrument independent of sample electromagnetic properties[J].NDT&E International,2012,48:16-22.
[10]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2005.
