红外瓦斯传感器检测中噪声点研究*
2015-04-01程文娟黄星星汤世祥周淼淼
程文娟,黄星星,汤世祥,童 兵,周淼淼
(合肥工业大学 计算机与信息学院,安徽 合肥230009)
0 引 言
常用煤矿瓦斯检测仪按其工作方式可分为催化型、热传导式、气敏半导体型和红外型等[1]。但是催化型存在零点漂移和灵敏度衰减的问题[2]、热传导式易受到水蒸汽等其他气体的影响、气敏半导体型的测量范围窄而且精确度低。因为红外型瓦斯检测仪具有测量范围广、响应速度快、寿命长、不易中毒等优点已被广泛应用于煤矿环境中易燃易爆气体浓度的检测[3]。但由于红外瓦斯传感器检测仪易受煤矿环境中的温度、湿度、压力等复杂的物理环境因素影响,使检测瓦斯浓度值不准确,一般有硬件和软件两种方法来解决这一问题。但由于通过硬件改进的方法价格昂贵,一般倾向于采用软件方法。近些年有很多文献撰写了关于采取软件的方法设计红外瓦斯传感器,如参考文献[4~6]等,其中较为经典的软件方法是参考文献[4]所述选用防脉冲平均滤波算法,该算法的基本思想是去掉n个采集数据集中最大值和最小值,然后计算剩下所有样本的平均值。此方法比较简单且易行,但存在着如果采集数据量n 值偏大时灵敏度会降低的缺点。参考文献[5]用线性最小二乘法分别计算出采集数据集中的最大和最小的理想值,将最大和最小理想值的差值带入相应公式计算出瓦斯浓度值。这样不仅保证数据的连续性,而且具有较高检测响应时间,但该方法工作效率低。参考文献[6]基于RBF 神经网络对采集数据处理,这种方法能够消除环境中温度和湿度因素对瓦斯浓度检测的影响,但没有考虑其他物理环境和硬件本身因素对瓦斯浓度测量值的影响。
本文将与基准数据偏差较大的点定义为噪声点。首先,利用分化距离与K-means 算法结合方法找出采集数据中可能的噪声点;其次,根据孤立度系数判断真正的噪声点;再次,对噪声点做直接丢弃处理,这样做可以提高软件工作效率;最后,对处理之后的剩余采集数据集计算平均值即为测量的瓦斯浓度值,实验结果表明:该方法测试出的瓦斯浓度的误差小于1%,精度高。
1 相关理论
1.1 朗伯—比尔定理
红外型瓦斯传感器是基于分子振动和转动吸收谱与发光光谱的一致性原理而制成的[7]。当红外光透过待测气体时,红外光的强度会变弱,气体对红外光的吸收遵循朗伯—比尔(Lambert-Beer)定律

式中 I 为透射光强度;I0为入射光强度;K 为吸收截面系数;L 为红外光透过气体层的厚度;C 为待测气体的浓度。根据入射光和透射光的强度便可计算出气体的浓度C。
1.2 分化距离
分化距离是指计算任意两数据点的实际距离D(i,j)和任意两点距离中最大距离dmax,选取分化度φ(0 <φ <1),对所有的D(i,j)做分化处理,便得到分化距离d(i,j)[8],其关系式为

式中 d(i,j)为分化距离;φ 为分化度;D(i,j)为两点间实际距离。任意两点距离D(i,j)与距离集中最大距离dmax的比值Θ(i,j)为

式中 D(i,j)为两点间实际距离;dmax为距离集中的最大距离。如果Θ(i,j)<φ,则D(i,j)<d(i,j);否则D(i,j)≥d(i,j),分化距离的思想是使原本能靠近的两个数据更紧密,原本距离较远的两个数据变得更远。
1.3 K-means 算法模型分析
K-means 算法是关于数据集相似度的聚类算法,是一种非监督学习方法[9]。在中小规模的样本数据的聚类采用此方法有很好的效果。
根据参考文献[10]中所述K-means 算法主要思想,首先,需要随机选取初始聚类的K 个中心点;其次,计算所有剩余的数据集到中心点的欧氏距离,将距某一中心点最近的数据点归并到该聚类;最后,用均值法调整聚类的中心点计算收敛函数,不断重复上述步骤,直至收敛函数的值最小为止。
对于一系列时间间隔相同的数据点,可将K-means 算法的思想简化为如下步骤:
1)在数据集D 中随机的选择K 个点β1,β2,β3,…,βk作为聚类簇C1,C2,C3,…,CK的聚类中心点;
2)计算不在聚类簇的数据集中的点di各个簇类中心点的欧氏距离,并将距di最近的点分配到Cj类

3)对于簇Cj,重新计算簇Cj的质心βj;
4)计算收敛函数,并判断收敛函数的值是不是最小,其中收敛函数如式(5)所示

2 采集数据处理与模型建立
实验设计红外瓦斯传感器选用单光路双波长的设计方案,红外瓦斯传感器系统示意图如图1 所示。

图1 红外瓦斯传感器系统示意图Fig 1 Diagram of infrared gas sensor system
红外瓦斯传感器系统中光源为IRL715;探测器为PYS3228,该探测器含两个独立的滤光片和探测器。其中,单片机不仅控制光源调制电路和光源驱动电路,而且可以显示检测的瓦斯浓度值。
用实验设计的系统采集120 个数据作为采集数据集D={x1,x2,…,xi…,x120},将此120 个数据分为3 组,每组40 个数据点,首先,计算相邻两个数据xi,xi+1绝对值ai,绝对值的集合为A={a1,a2…,ai,…,a39},如果相邻数据差的绝对值较小,则这两个数据点很可能是在同一聚类簇中;其次,对集合A 中的数据点做分化距离处理后得到的集合S={s1,s2,…,sx,…,s39};最后,用K-means 算法对集合S进行聚类,可得到不同的聚类簇中心值和各个聚类簇中的数据点,选择聚类中心点值最大的簇作为虚拟噪声点的集V={d1,d2,…,dm}。
根据虚拟噪声集合V 中数据点查找在集合D 中对应的数据值,求出这些数据点的前后相邻数据点的孤立系数,并分别将某一数据点与其前后相邻的数据点计算的孤立系数的值分别叫前孤立系数和后孤立系数。孤立系数的表达式为

式中 xi与xi+1为相邻的两数据点,f 为采样频率。将θ 与给定的阈值ε 比较,如果θ≥ε,则孤立度高;否则,孤立度低。
如果一个数据点的前孤立系数和后孤立系数均大于阈值ε,则此数据点为噪声点,如果一个数据点与其前相邻的孤立系数高与其后相邻的孤立系数低,或者相反,如图2 所示,可将其视为转折点。

图2 转折点示意图Fig 2 Diagram of turning point
根据以上设想,将某一数据点的前、后孤立系数与给定的阈值比较,即可判断此数据点是不是噪声点。可用如表1所示的噪声点判定表判断。

表1 噪声点判断表Tab 1 Noise point determination
如果判定xi是噪声点,可以直接将其丢弃,假设噪声点有m 个,分别为{x1,x2,…,xm},丢弃噪声点之后的有用数据为{x1,x2,…,x40-m},选用式(7)均值法计算浓度值

通过上述对数据集处理过程的描述,得到样本处理点的流程图如图3 所示。

图3 样本处理流程图Fig 3 Flow chart of sample processing
3 实验结果与分析
本文中K-means 算法中K=4,f=0.5 Hz,根据经验可知孤立系数阈值为ε=arctan 0.03,分化度为φ=0.01。
本文选取浓度为2%的标准瓦斯浓度分别选用基于分化距离与K-means 算法结合的方法处理采样值与不做任何处理采样数据集可得到如图4 所示的实验结果对比图。由图4 可以看出:基于分化距离与K-means 结合的方法处理数据集之后的数据集中的噪声点明显比不做任何处理的采集数据集中的噪声点的数目减少,所以,此方法检测的瓦斯浓度值的准确度高。
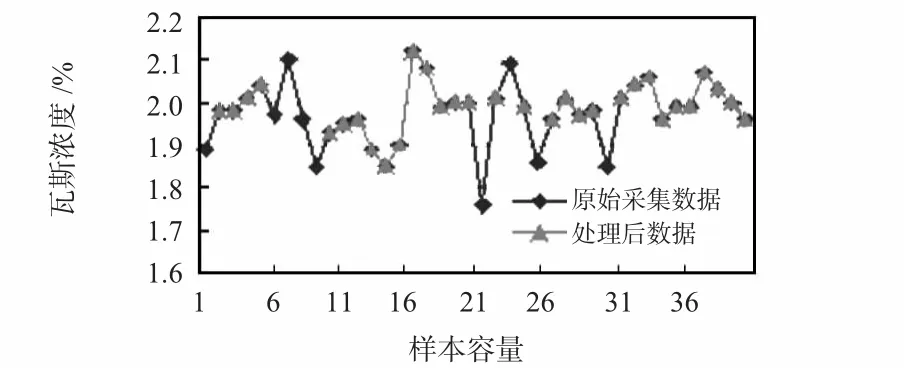
图4 实验结果对比图Fig 4 Comparison of experimental results
本文对标准瓦斯浓度的选取值小于5%,经过采用基于分化距离与K-means 算法结合方法,通过聚类和判断噪声点等过程的处理,可得实验结果对比分析表如表2。

表2 实验结果对比分析表Tab 2 Comparison and analysis of experimental results
从表2 可以看出:基于分化距离与K-means 算法结合方法检测瓦斯浓度小于1%,而且具有较高的精确度。
4 结束语
本文提出了一种基于分化距离与K-means 算法结合的方法,对采集一段时间采集数据集处理,再根据前后孤立系数判断噪声点,计算浓度值。经过实验证明了此方法的有效性,由实验结果可看出:此方法检测的瓦斯浓度值小于1%,测量精确度高,适用于矿井的复杂环境。除此之外,本方法还可应用于其他气体测试。
[1] 张 雷,尹王保.基于红外光谱吸收原理的红外瓦斯传感器实验[J].煤炭学报,2006,31(4):480-483.
[2] 于 震,张正勇.热催化瓦斯传感器的特性及其补偿方法[J].传感器与微系统,2010,29(1):42-44.
[3] 叶玮琳,郑传涛.中红外甲烷检测仪稳定性实验及温度补偿研究[J].光学学报,2014,34(3):273-277.
[4] 吕光洁.光谱吸收式煤矿瓦斯红外检测技术的应用研究[D].西安:西安科技大学,2009.
[5] 赵 聪.基于非色散红外光谱吸收原理的瓦斯浓度检测仪设计[J].计算机测量与控制,2009,17(6):1229-1231.
[6] 张 丽,王汝琳.基于神经网络的矿用红外瓦斯传感器检测模型的研究[J].工矿自动化,2009(8):18-21.
[7] 罗达峰,杨建华.基于红外吸收光谱的瓦斯气体浓度检测技术[J].光谱学与光谱析,2011,31(2):384-386.
[8] 刘 欢,吴介军.基于分化距离的离群点检测算法[J].计算机应用研究,2010,27(9):3316-3318.
[9] Han Jiawei,Kamber Micheling,Pei Jian,et al.数据挖掘概念与技术[M].范 明,孟小峰,译.北京:机械工业出版社,2012.
[10]周爱武,于亚飞.K-means 聚类算法的研究[J].计算机技术与发展,2011(2):62-65.
