基于信息熵的多无源传感器数据关联*
2015-04-01王朝英孔云波刘玉军鹿传国
曹 乐,王朝英,孔云波,刘玉军,鹿传国
(1.空军工程大学 信息与导航学院,陕西 西安710077;2.95806 部队,北京100086)
0 引 言
无源传感器具有良好的隐蔽性、抗电磁干扰、抗反辐射导弹等优点[1],近年来已被广泛研究,成果日益增多[2~5]。但无源传感器的量测信息仅包含角度信息,加大了数据关联的难度,利用几何交叉定位技术对空间目标进行定位则产生了大量的虚假点[6],且随着传感器与目标数目的增多呈指数级增加。
为解决多无源传感器跟踪中数据关联问题,Bar-Shalom Y 等人将其描述为一个多维分配问题。Pattipati K R 在文献[7]中提出利用量测与伪量测的极大似然比构造关联代价函数,并利用多维分配模型求解最优划分。但该代价函数仍难以精确反映量测数据间的关联的可能性大小,且当维数高于二维时,多维分配问题计算复杂度高,无法求得最优解。因此,目前的大部分研究多致力于降低该模型的复杂度,如文献[3]提出了约减关联假设空间的二面角聚类算法;文献[8]利用方位角和俯仰角信息筛选可能的关联组合,通过指示函数分析挑选出正确关联组合;文献[9]根据最大似然算法将定位问题转化为无约束的优化问题;文献[10]推导了基于测向线的关联依据,提出了两级消元式数据关联算法。以上方法都是利用先验信息来减小搜索区域以降低计算复杂度,从分配方式角度改进算法,而忽略了关联代价函数的构造。
文献[11]明确指出极大似然法[7]在构造代价函数时忽略了极大似然估计所引入的误差,可以通过修正代价函数增强模型的完备性以提高关联正确率。因此,本文从增强多维分配模型完备性的角度,提出基于信息熵的多无源传感器数据关联算法。信息熵可以有效地度量相似概率密度函数之间的差异,充分考虑到极大似然估计所引入的随机误差。本文利用最常用的两种信息熵:相对熵和Renyi熵度量伪量测的概率密度函数与真实量测数据的极大后验分布[4]之间的相似性,构造关联代价函数。最后通过仿真实验对本文算法进行验证,进一步证明了该算法的有效性。
1 问题模型
假定在观测区域内有M 个目标,通过N 只传感器进行协同目标定位。图1 即表示目标j 与传感器之间的关系模型。其中,传感器s 的坐标,目标j 的坐标

图1 多无源传感器目标跟踪模型Fig 1 Multi passive sensor target tracking model
1.1 量测模型
根据图1 所示的模型,传感器s 测得目标j 的角度量测为θsj=[βsj,αsj]T,其中

每只传感器均允许漏检与虚警,则传感器的量测模型可以表示为

其中,量测噪声服从正态分布,即vsi~N(0,Rs),虚警在观测区域近似服从均匀分布,psj=1/φs。
为简化由漏检引起的不完全测量与目标的互联,为传感器s 引入一个虚拟量测ms0,则传感器s 获得的量测集合可以表示为,所有传感器获得的量测数据表示为
1.2 多维分配模型
数据关联即识别真实目标的数目并估计目标的位置,同时对量测集合进行可行性划分。设γ 为一可行划分,Ψ={γ}为所有可行划分的集合,数据关联即是寻找到Ψ中的最优划分γest,通常利用多维分配算法求解。
传统多维分配算法是利用量测与伪量测间的统计距离构造关联代价,即

其中,PDs为传感器s 的检测概率,δ0is为狄拉克函数,为某关联假设下目标的伪量测与量测的统计距离。
定义 ρi1i2…iN为二元变量,表示分配的量测集合是否与目标互联,则完整的多维分配模型表述为

满足约束条件

1.3 目标位置估计
为获得目标伪量测信息,首先要确定目标的位置估计信息。不考虑量测噪声的影响,根据式(1)和式(2)将N 只传感器的量测方程用矩阵形式表示为

其中

则利用伪线性最小二乘定位算法[12]求得目标位置估计为

对应的估计协方差阵为

2 基于信息熵的数据关联
信息熵是对事件不确定性的一种度量。若P,Q 分别表示两个连续的随机变量,其概率密度函数分别为p(x),q(x),则随机变量P 的信息熵H(P)可以表示为
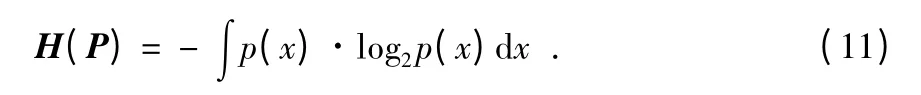
条件信息熵表示在某个变量确定的前提下,其它未知变量所包含的信息量,表示为

其中,H(Q,P)表示变量P,Q 的联合熵。条件熵表示两个变量之间的相关程度,因此,可以利用条件熵度量目标真实位置与极大似然估计之间的相关性程度,修正关联代价函数,以提高关联正确率。本文主要利用两种常用的信息熵:相对熵与Renyi 熵对关联代价函数进行修正。
2.1 伪量测统计特性
关联代价函数的构造为数据关联的核心,而修正代价函数首先即要确定伪量测的统计特性。无迹(UT)变换是计算随机变量经非线性变换后统计特性的方法,因此,本文采用对称采样的UT 变换[13]求解伪量测的统计特性。
基于式(1),式(2)所述的传感器观测模型,记xj与对应于传感器s 的伪量测~mj之间的映射关系为

1)Sigma 点采样:采用对称采样确定目标位置估计的Sigma 点集

采样点对应的权值为

其中,i=0,1,…,2n(n 为x^j的维数)为比例系数,调节Sigma 点与均值的距离。
2)非线性变换:将Sigma 点ηi按式(13)进行非线性变换得点集
3)数值计算:伪量测的均值和方差分别为

2.2 基于相对熵的关联代价
相对熵是描述两个随机变量P,Q 之间差异的一种方法,利用其可以度量不同概率密度函数之间的差异,则两个一维连续随机变量之间的相对熵定义为

由于相对熵不满足交换律,不是严格意义上的距离信息。因此,利用对称相对熵构造关联代价函数。对称相对熵定义如下
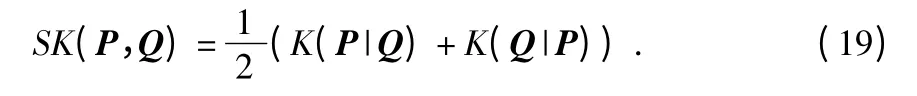
假设不同传感器之间的观测相互独立,考虑漏检和虚警的影响,则对应关联假设的代价函数为

代价函数的核心即相对熵的计算,假设P,Q 均服从高斯多维分布,即p ~N(μ0,∑0),q ~N(μ1,∑1),则相对熵可化简为

2.3 基于Renyi 熵的关联代价
Csiszar 在20 世纪60 年代前后提出f 散度的概念,定义为

f 散度是通过f 函数对散度进行调节,不同的f 函数,对应着不同的散度。当f 函数取时,代表f 散度的一种特殊的情况—Renyi 熵,定义为
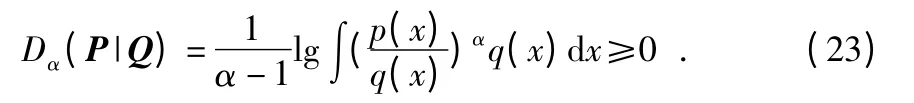
其中,α 为Renyi 熵参数(α∈(0,1))。
Renyi 熵同样不是严格意义上的距离信息,因此,定义对称Renyi 熵如下

则对应关联假设Mi1i2…iN的代价函数为
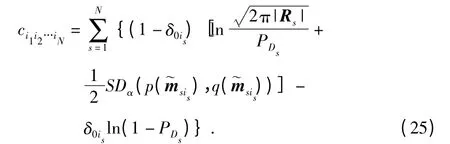
其中,Renyi 熵的表达式可以化简为

将上式结果代入式(25)即修正关联代价函数。
3 仿真实验
为验证本文所提算法的正确性,对相同配置方案下本文算法与文献[7]算法进行比较分析。由于多维分配算法是一典型的NP 难题,实验中的多维分配问题均利用线性松弛法[14]求解。
本仿真设置2 只无源传感器,其坐标分别为(20,0,0.1)km,(0,20,0.1)km,目标在以探测器为中心,半径为20 km 的球形区域内产生。不考虑漏检和虚警,在传感器角度量测误差标准差为1,3,5 mrad 的情况下分别进行仿真。由于α=0.5 时Renyi 熵能够充分考虑到两个相似概率密度函数之间的最大差别[15],因此,以下仿真实验中 的值均取0.5。
3.1 两目标关联
假设在观测区域内有2 个目标,坐标分别为(x,y,z)和(x+d,y,z)。其中,d 为两目标之间的距离,在[0.05,2]km之间每隔0.1 km 进行取值,蒙特—卡罗仿真次数取1 000。仿真结果如图2,由图可以看出:随着量测噪声的增加,目标关联正确率明显下降,同时,随着目标间距的增大,关联正确率逐渐提高。利用信息熵构造关联代价函数,相对于文献[7]算法明显提高了关联正确率,且基于Renyi 熵的改进效果优于基于相对熵的改进。

图2 两目标关联正确率曲线Fig 2 Association accuracy curve of two-target
3.2 多目标关联
假设在观测区域内有5,10,15 个等间隔排列的目标,相邻目标之间的间隔为d,蒙特—卡罗仿真次数取500。表1 ~表3为不同目标间隔、不同量测误差下各算法的关联正确率。表中数据进一步证明了利用信息熵修正关联代价函数的有效性,与文献[7]算法相比,相对熵改进算法关联正确率提高了1.5%~5.8%,平均提高了近3.7%;Renyi 熵改进算法关联正确率提高了2.2%~7.5%,平均提高了近5.2%。

表1 5 目标关联正确率Tab 1 Association accuracy ratio of five-target

表2 10 目标关联正确率Tab 2 Association accuracy ratio of ten-target

表3 15 目标关联正确率Tab 3 Association accuracy ratio of fifteen-target
3.3 算法复杂度分析
表4 为2 只传感器跟踪2 个机动目标时不同算法计算关联代价的相对运算强度。由表中数据看出:基于信息熵的算法增大了算法运算强度,提高了关联的复杂度,分析其主要是由于伪量测统计特性计算。基于相对熵的改进算法计算复杂度相对较低,更适于实际应用。

表4 相对运算强度Tab 4 Relative computing intensity
4 结 论
本文将伪量测视作随机变量,利用信息熵度量量测与伪量测概率密度函数之间差异构造关联代价函数,以增强模型的完备性,提高关联的性能。仿真实验表明:该方法充分考虑了极大似然估计引入的误差,更精确地反映数据关联的可能性程度,有效地提高了数据关联的正确率。其中利用Renyi 熵修正关联代价函数改进效果更明显,但其计算复杂度相对于相对熵方法略有提高。
[1] Musicki D.Multi-target tracking using multiple passive bearingsonly asynchronous sensors[J].IEEE Trans on Aerospace and Electronic Systems,2008,44(3):1151-1160.
[2] Ouyang C,Ji H.Improved relaxation algorithm for passive sensor data association[J].IET Radar,Sonar and Navigation,2012,6(4):241-250.
[3] Zhang S,Bar-shalom Y.Efficient data association for 3D passive sensors:If I have hundreds of targets and ten sensors(or more)[C]∥Fusion 2011 14th International Conference on Information Fusion,Chicago,IL,United States,2011:1-7.
[4] 鹿传国,冯新喜.基于Kullback-Leibler 散度的无源传感器数据关联算[J].吉林大学学报:工学版,2013,43(6):1404-1408.
[5] 田 野,姬红兵,欧阳成.基于距离加权最小二乘的量测数据关联[J].系统工程与电子技术,2011,33(11):2353-2358.
[6] Lidgren A G,Gong K F.Properties of bearing-only motion analysis estimator:An interesting case study in system observability[C]∥Proceedings of the 12th Asilomar Conference on Circuits Systems,and Computer Monterey,CA,USA,1978:50-58.
[7] Pattipati K R,Bar-shalom Y.A new relaxation algorithm and passive sensor data association[J].IEEE Trans on AC,1992,37(2):198-213.
[8] 田 野,姬红兵,欧阳成.基于角度余切值的多被动传感器数据关联[J].电子与信息学报,2010,32(10):2331-2335.
[9] 王燊燊,冯金富.基于角度信息的近空间雷达网定位算法[J].空军工程大学学报,2012,13(1):33-37.
[10]蒋文涛,孙利民,吕俊伟.面向测向交叉定位的2 级消元数据关联算法[J].华中科技大学学报:自然科学版,2012,40(3):63-67.
[11]Ouyang C,Ji H.Modified cost function for passive sensor data association[J].Electronics Letters,2011,47(6):383-385.
[12]王 鼎,张 莉,吴 瑛.基于角度信息的约束总体最小二乘无源定位算法[J].中国科学E 辑:信息科学,2009,36(8):880-890.
[13]Julier S J,Uhlmann J K.A general method for approximating nonlinear transformations of probability distributions[R/OL].[2004—03—13].http:∥www.robots.ox.ac.uk/siju/work/Publications/letter-size/Unscented.zip.
[14]Sunsil Mathews.An efficient implemen-tation of a batch-oriented,multi-target,multidimensional assignment tracking algorithm with application to passive sonar[R].Island:Naval Undersea Warfare Center Division Newport,2011.
[15]Yang C,Kadar I,Blasch E.Comparison of information theoretic divergences for sensor managment[C]∥SPIE Defense,Security,and Sensing,International Society for Optics and Photonics,2011:80500C1-80500C10.
