基波相位补偿脉冲输出式流量计检定新方法
2015-04-01刘桂雄
杨 茹 刘桂雄 万 勇 黄 坚
(广州能源检测研究院1,广东 广州 510170;华南理工大学机械与汽车工程学院2,广东 广州 510640)
0 引言
脉冲输出式流量计输出信号简单、抗干扰性强、易于传输,在生产实际中得到广泛应用,一般采用测频法对其进行检定。测频法包括直接测频法、模拟内插法、游标法、脉冲衰减法、多周期同步法、全同步法等。其中,最常用的直接测频法测量结果含±1 个字的计数误差。模拟内插、游标法与脉冲衰减法也是高精度时间数字转换器常见的设计方法,但对于流量计100 μs ~100 ms 范围脉冲间隔时间的测量,这些方法存在电路规模大、动态范围有限及易受干扰脉冲影响等问题[1-4]。多周期同步法被测信号和闸门信号同步,消除了被测信号±1 个字计数误差,但基频信号仍存在±1 个字的计数误差[5]。全同步法实质是一种相位同步法,其消除了基频误差,但测量时间长,且无法进行多路测量[6-8]。为解决目前脉冲输出式流量计无法多路测量、检测精度低、测量结果受干扰脉冲影响及高精度频率测量需要基频信号发生装置等问题,文中研究了一种基于脉冲基波相位测量的多路不同步脉冲计数补偿新方法。
1 多路脉冲计数补偿原理
流量计输出脉冲频率f 与流过管道的体积流量q成正比,K=f/q 为仪表系数。考虑流量q 范围及各类流量计仪表系数K,流量计输出频率f 范围为10 ~10 kHz。按照国家计量检定规程,容积法、标准表法或称重法,检定装置均有最短检定时间tmin限制,即检定时间tm>tmin。图1 为多路脉冲与闸门信号波形图,各路信号与闸门信号不同步,因而均存在±1 个字的计数误差。集成检定多台流量计时,为保证检定效率,tm不能过大,因此脉冲输出频率低的流量计检定结果相对误差大。
各类能提高精度的方法,具体技术手段均是通过减小闸门信号与相邻脉冲上升沿时间差来减小计数误差。相位补偿原理与之近似,图2 为通过获取脉冲信号在闸门信号发生时刻相位φ 进行精度补偿的原理示意图。

图1 多路脉冲与闸门信号波形图Fig.1 Waveforms of multi-channel pulse and gate signal

图2 脉冲信号相位补偿原理图Fig.2 The principle of pulse signal phase compensation
设脉冲信号周期为T,脉冲信号在闸门信号发生时刻t1、t3的相位分别为φs、φe。根据图2,有φs=(t1-t0)/T、φe=(t3-t2)/T,则需补偿计数值Nc为:
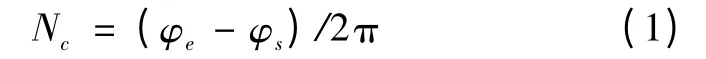
按上升沿跳变模式计数,设在测量时间内测得的脉冲个数值为Np,则经计数补偿后的精确计数值N 为:

多路脉冲补偿的原理是:对任意i 路脉冲信号进行测相处理,获取其在计数启停时刻的相位φsi、φei,并根据式(1)、(2)进行计数补偿。然而,流量计受现场机械振动及流场不稳定因素影响,其输出信号可能存在干扰脉冲。因而,通过直接测量t1-t0、t3-t2计算相位进行精度补偿方法可能会恶化测量结果。自适应陷波滤波器(adaptive notch filter,ANF)可自动使陷波频率跟随输入信号频率变化,抑制噪声,并可提取信号幅值、频率、相位,其在理论研究及工程应用上都受到广泛重视[9-14]。下面讨论自适应陷波器提取脉冲计数起止时刻基波信号相位的具体实现方法。
2 周期脉冲信号相位提取技术
ANF 虽然是理论研究及工程应用热点,但Regalia提出的ANF 受正弦信号幅值、频率相互高度耦合的影响,频率估计暂态响应速度受幅值大小影响[9]。Liu 在Regalia 基础上设计了一种收敛速度不受幅值影响的全局收敛归一化ANF,但仅能处理单正弦输入信号[10]。Mohsen 研究的固定自适应增益γ 的ANF[11]能很好地处理受谐波干扰的正弦输入信号,近年来获得广泛工程应用[12-14],但该ANF 不能很好地提取周期脉冲信号的基波且收敛速度受幅值影响[14]。ANF 不能很好地处理周期脉冲信号的关键在于谐波叠加干扰,如能利用Butterworth 滤波器滤除5 次谐波及以上分量,则能为ANF 提供更高信噪比的输入信号。脉冲信号相位提取流程框图如图3 所示。
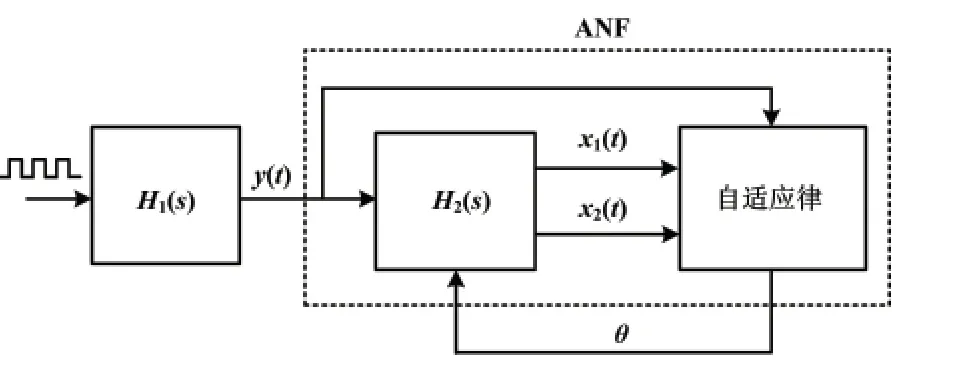
图3 脉冲信号相位提取流程框图Fig.3 The phase extraction process of pulse signal
2.1 数字Butterworth 滤波器设计
Butterworth 滤波器在线性相位、衰减斜率和加载特性三方面特性均衡。其频率归一化传递函数为:
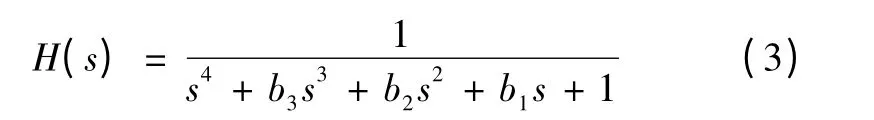
式中:b1=2.613 1;b2=3.414 2;b3=2.613 1。
设采样间隔时间为Ts,ωi为第i 路脉冲信号角频率,Butterworth 低通滤波器截止频率ωci为2ωi,则第i路信号Butterworth 低通滤波器非归一化传递函数为:

利用Z 变换对式(4)离散化,令u(k)、y(k)为k 时刻离散形式滤波器的输入、输出,则有:
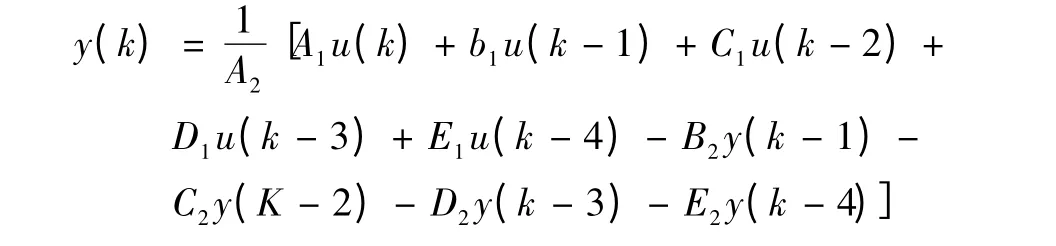
式 中:A1、A2、B1、B2、C1、C2、D1、D2、E1、E2为 与ωci、Ts、b1、b2、b3相关的常数。
2.2 自适应陷波器脉冲信号提取
令f 为输入信号,二阶系统状态变量为x1、x2,阻尼比为ξ,自适应增益为γ,角频率ω 瞬态估计值为θ,那么可设计ANF 为[11]:

若不考虑式(6)自适应率,式(6)传递函数为:
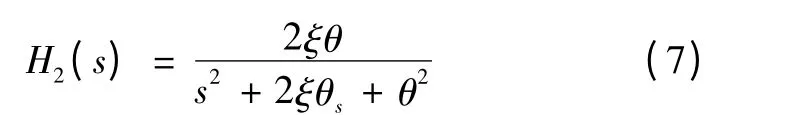
令Butterwoth 数字滤波器滤波后周期脉冲基波信号为y(k)=Asin(ωkts+φ),则离散化ANF 为:

对于第i 路周期输入信号,假设动态系统(5)、(6)在ts时刻进入其周期轨道,则∀n >[ts/Ts],动态系统(5)、(6)具有唯一周期轨道[11]:
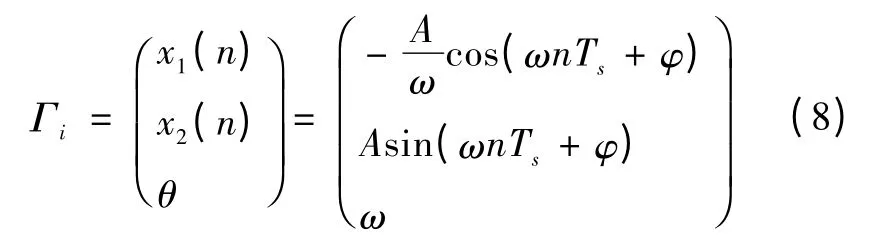
因而,根据周期轨道Γi,状态变量x2与输入信号y 完全一致,并可通过Γi求得脉冲信号在任意n 时刻的相位:
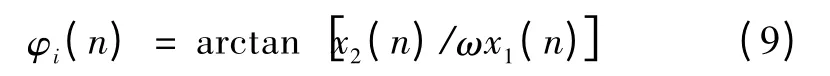
按式(9)求得闸门信号发生时刻t1、t3时脉冲信号的实时相位分别为φs、φe。由于式(1)为差分结构,并且流量计检定过程中有保持供水压力恒定的要求,因而利用式(1)求补偿计数值Nc时可不考虑低通滤波导致的相位损失。
3 仿真及试验
3.1 仿真试验
设关于时间轴对称的周期脉冲信号f(t)幅值为A,角频率为ω,那么其傅里叶级数展开式为:
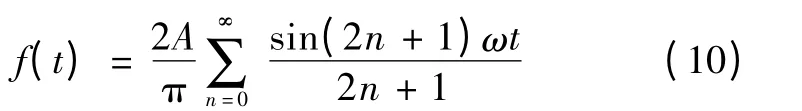

图4 周期脉冲信号相位仿真试验结果Fig.4 Results of periodic pulse signal phase simulation experiment
图4(a)为Butterworth 滤波曲线图,周期脉冲信号经过滤波,相位有一定滞后,并在正弦基波基础上叠加了3 次谐波。
图4(b)为ANF 频率收敛曲线,前置Butterworth滤波后,频率跟踪0.75 s 即可收敛至稳态,克服了谐波干扰对收敛的影响。
图4(c)为ANF 输入与状态变量x2的曲线图,表明ANF 在谐波干扰不严重前提下可有效提取周期基波信号。
图4(d)为ANF 状态变量x1、x2稳态曲线图,可看出对于周期脉冲信号输入,正弦度好、相位差90°,与预定周期轨道相符。因而,易根据x1、x2及式(9)求得输入信号y 在任意时刻的相位。
3.2 计数补偿效果试验
实验平台为DN10 -20 双台位流量计检定装置,在其上位机上配置转换精度16 位、最高采样频率250 kHz的阿尔泰PCI 8602 型数据采集卡。数据采集卡接入2 台流量计及2 台标准表输出脉冲信号(标准表频率分别为6 Hz、80.1 Hz)。利用上升沿检测手段检测4 路脉冲信号并对6 Hz 信号实现整周期截取,产生48 s标准时间信号,以满足tm>tmin检定时间要求。调节流量计脉冲当量,使其输出100 ~800 Hz 的信号。上位机对输入脉冲信号振幅做±1 处理,并乘π/4,即输入信号基波为y =sin(ωt +φ)。在算法开始运行前对流量计信号进行测周处理,并据此预设4 阶Butterworth 低通滤波器通带角频率ω0,ANF 角频率估计初值θ0。ANF 阻尼比ξ =0.15,自适应因子γ =5。表1 为4 组3 路输入脉冲信号进行计数补偿试验数据。从表1 可看出,上升沿检测法计算所得脉冲个数均存在±1 个字的计数误差,经补偿后计数误差均小于±0.06个。上位机通过写dat 文件保留现场运行数据。
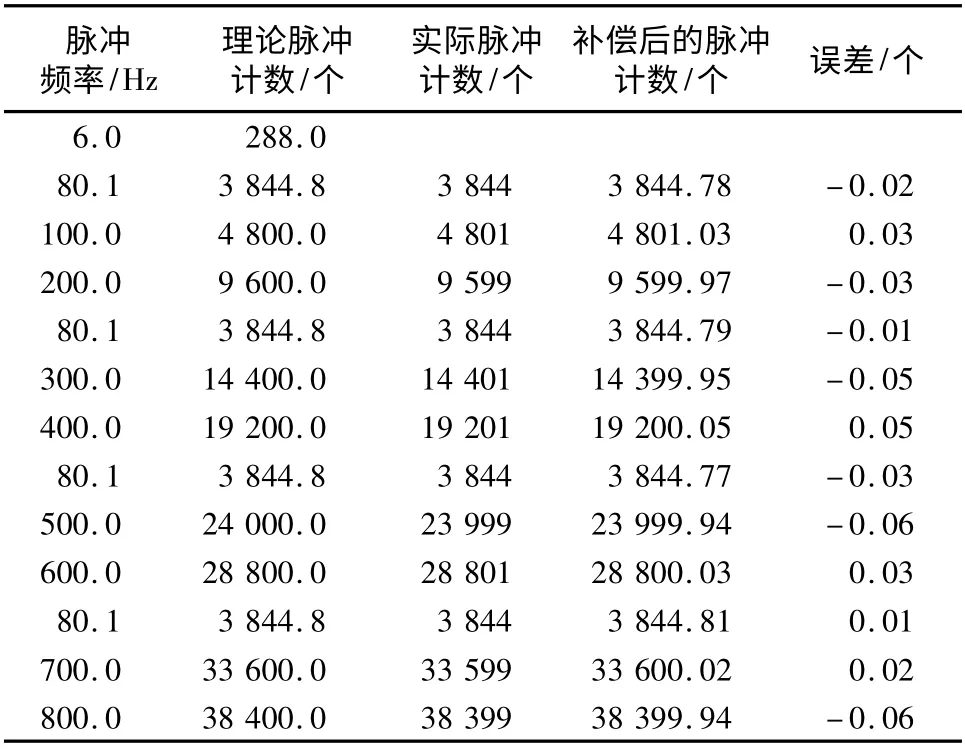
表1 计数精度补偿试验数据Tab.1 Experimental data of counting precision compensation
图5 为根据现场运行数据还原的输入响应曲线与角频率估计曲线。其中,图5(a)为状态变量x1、x2在200 Hz 脉冲输入时的响应曲线,图5(b)为频率估计值收敛曲线。
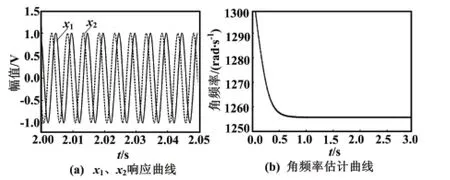
图5 输入响应与角频率估计曲线Fig.5 Input response and angular frequency estimation curves
4 结束语
为实现脉冲输出式流量计多台位高精度检定,提出并实现了一种基于基波相位补偿的新方法。理论仿真
与试验验证表明:①采用前置数字Butterworth 滤波器的方法提高抗谐波干扰能力,可很好地限制无限次奇次谐波叠加引起的干扰;②配合前置测周,预估角频率周期,角频率收敛速度快,自适应陷波器可在1 s内进入其周期轨道,获取准确基波相位时间短;③频率、相位估计准确性在多路脉冲计数补偿中得到验证,3 组不同步计数补偿试验说明计数误差小于±0.06 个。这种通过实时计算信号相位进行计数补偿方法能有效提高脉冲计数检定精度,提高多路并行检定的实用性。在检定装置流场稳定情况下补偿方法效果良好,对在流场不稳定的情形下实现多台位高精度检定还需进一步研究。
[1] Jansson J P,Mantyniemi A,Kostamovaara J. Synchronization in a multilevel CMOS time-to-digital converter[J].Circuits and Systems I:Regular Papers,IEEE Transactions on,2009,56 (8):1622 -1634.
[2] Markovic B,Tisa S,Villa F A,et al. A high-linearity,17 ps precision time-to-digital converter based on a single-stage Vernier delay loop fine interpolation[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2013,60(3):557 -569.
[3]Vercesi L,Liscidini A,Castello R.Two-dimensions vernier time-todigital converter[J].Solid-State Circuits,IEEE Journal of,2010,45(8):1504 -1512.
[4] Chen C C,Lin S H,Hwang C S.An area-efficient CMOS time-todigital converter based on a pulse-shrinking scheme[J]. IEEE Transactions on Circuits and Systems Ii-Express Briefs,2014,61(3):163 -167.
[5] 张志文,王承林,王伟,等. 新型多周期同步和倍频锁相的频率跟踪技术[J].电力系统及其自动化学报,2009(5):119 -123.
[6] Du Baoqiang ,Wang Yanfeng ,Zhou Wei ,et al. Ultra -resolution phase comparison method combining phase synchronous detection and common frequency source[J]. Measurement,2013,46(1):374 -377.
[7] 杜保强,左艳迪,周渭,等. 优于皮秒分辨率的特高频率测量方法[J].北京邮电大学学报,2013(6):84 -88.
[8] 杨茹,潘云飞,万勇,等. 双台位流量计检定装置脉冲计数精度补偿方法:中国,201410579278.9[P]. 2015.01.07.
[9] Regalia P A. An improved lattice-based adaptive IIR notch filter[J].Signal Processing,IEEE Transactions on,1991,39(9):2124-2128.
[10]Hsu L,Ortega R,Damm G. A globally convergent frequency estimator[J]. Automatic Control,IEEE Transactions on,1999,44(4):698 -713.
[11]Mojiri M,Bakhshai A R. An adaptive notch filter for frequency estimation of a periodic signal[J]. Automatic Control,IEEE Transactions on,2004,49(2):314 -318.
[12]Mojiri M,Karimi-Ghartemani M,Bakhshai A. Time-domain signal analysis using adaptive notch filter[J]. Signal Processing,IEEE Transactions on,2007,55(1):85 -93.
[13]刘桂雄,黄坚,江境宏.一种抗强谐波干扰的多台位流量计脉冲计数补偿方法:中国,201510358402.3[P].2015.09.09.
[14]Fedele G,Ferrise A.A frequency-locked-loop filter for biased multisinusoidal estimation[J]. Signal Processing,IEEE Transactions on,2014,62(5):1125 -1134.
