微反应器流道内单气泡逸出动力学模拟

季 炜，周 吉，吴太军

(1．重庆三峰环境产业集团有限公司 国家环境保护垃圾焚烧处理与资源化工程技术中心，重庆 400084;

2．哈尔滨工业大学 能源科学与工程学院，黑龙江 哈尔滨 150001)

液体通流槽道内的气泡运动现象广泛存在于各类连续流式反应器中，其中气泡的生长脱离和迁移特性对流道内的质量、动量和能量交换、两相流动流型和流动阻力特性均有重要的影响。随着反应器向微型化、模块化的发展，反应器内流道尺寸进一步减小。由于受到壁面的影响，微小尺寸流道的气液两相流型、相分布、两相流动阻力特性将呈现与大尺寸槽道不同的特征和规律［1-2］。

Lutz［3］等研究单个气泡在矩形截面上升的现象，发现通道深度、气泡大小、叠加速度等参数的相互影响规律。Shaodan 等［4］等对竖直矩形窄缝通道内过冷沸腾水中气泡滑移特性研究后获得了流速、入口过冷度和热流密度对气泡滑移速度和气泡直径的影响。Jacqueline 等［5］研究了矩形微槽道内FC -72 流动沸腾时气泡生长、脱离及排出特性，分析了微槽内压降周期性波动与气泡生长过程的关系。在数值建模预测气泡形成方面，已有格子玻尔兹曼方法［6］、毛细方程数值积分法［7］等，近年来，VOF(Volume of Fluid)已在两相流动数值模拟中成功应用。Akbar 等［8］利用VOF 对竖直毛细管内Taylor 气泡迁移特性研究结果与实验结果和经验值均符合很好。Chakraborty 等［9］采用CLS -VOF 方法模拟静止液相和同向流动液相中气泡生长及脱离过程，与静止液相相比，同向流动的液相中气泡脱离加快，且气泡聚并行为得到抑制。目前关于不同槽道高宽比对液体通流槽道内单逸出气泡动力学特性影响的研究仍少见相关报道。

1 模型及方法

1．1 VOF 方法简介

VOF 方法通过求解单独的动量方程和处理穿过区域的每一流体的体积分数来模拟两种或两种以上不相混合的流体流动。两相间的界面通过计算每个网格中第k 相所占的体积分数Ck来追踪

且在任意网格中存在Ck通过连续性方程来求解，即

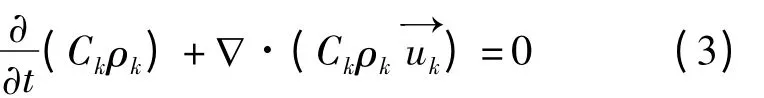
在微小槽道内的两相混合流动中，动量方程对各个流体相均适用，其速度场通过求解Navier -Stokes equation 获得

式中

p——静态压力;

u→——流体的速度场，u→=(u，v，w);

F→——动量源项，由表面张力产生;

ρ、μ——代表容积平均密度和动力粘度。

第一步:建立层次结构图。图1的指标体系图转化为层次分析中的层次结构图，将B2C电子商务企业成长能力分为目标层(A)、准则层(B)、因素层(C)和指标层。

式中下标g 和l 分别表示气相和液相。

动量源项的处理采用CSF(Continuum Surface Force)模型

计算区域内界面重构和界面推进采用分段线性重构方法，界面的位置由界面法向量n→和定义在网格中心的体积函数Ck确定，并采用Lagrangin 方法跟踪随流动传播的界面。界面曲率κk为

其中n→为

1．2 计算区域及网格划分

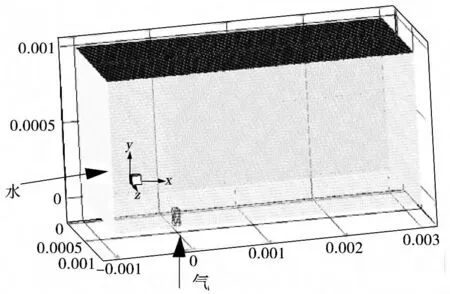
图1 计算区域的三维网格划分

本文构建了图1 所示三维矩形槽道模拟区域，采用ICEM 软件分块划分网格，利用O-grid 优化生成网格，实现区域间的平滑过渡。网格质量检测后显示所有模型的网格质量均达到0．4 之上，满足计算要求。网格进行无关性检验显示维持气、液流速不变，网格数目增大或减小50%时，计算结果(无论是槽道进出口压力，还是气泡的脱离体积)并无差异。由此认为此时的网格数是可行的。

1．3 边界条件及初始化

槽道左侧为液体入口，底部微孔(孔径:0．1 mm)为气体入口，两者均为质量流量入口边界条件。槽道右侧为出口，采用自由流出口边界条件。模拟中选取槽道长为4 mm，孔口位于底部中轴线上距离槽道入口1 mm 处。工质气相为空气，液相为水，两相温度均为300 K，表面张力系数为0．072 N/m。槽道内所有壁面接触角均为90°，所有壁面为无滑移边界。初始状态整个槽道内充满流动的不可压缩液体，液体流速维持0．1 m/s 不变，采用FLUENT6．3软件进行模拟，模拟工况如表1 所示。

表1 矩形微槽高宽比变化计算工况表

1．4 模型的验证

为了验证方法的正确性，利用本模型的计算结果与文献［10］的实验结果进行了对比，实验槽道尺寸为210 mm×2 mm×1．8 mm (长×宽×高)，液体流量恒定为10 mL/min，气体流量分别为0．1 mL/min，0．5 mL/min，1．0 mL/min，1．5 mL/min，气体逸出孔孔径为0．035 mm，4 种不同工况下数值计算获得的气泡脱离体积与实验获得的气泡脱离体积分别如图2 所示，二者的变化趋势均显示气泡脱离体积随着气体流量的增加逐渐增大，但趋势会减缓，对比结果显示气泡脱离体积的模拟值略小于实验值，但均在误差允许范围内。造成这一差异的可能原因之一是实验过程中入口气流的压力及质量流量不稳定，二是因为模拟中采用了不可压缩假设造成了数值计算误差，但总的看来对比结果显示本文中的数值模拟方法是可行的。

2 计算结果及分析

图2 模拟结果与实验结果对比

图3 显示了截面积1 mm2，不同高宽比时矩形槽道内气泡的生长和脱离现象。从图3(a)可知，当高宽比为4∶1 时，气泡从孔口冒出后会迅速向周围扩张，由于槽道宽度较小，气泡生长时会很快粘附上槽道一侧壁面(0．0072 s);随着气泡体积的进一步增加，与槽道两侧壁面均发生接触(0．0216 s)，并呈现出半圆柱形状，将槽道底部的一段连续面积完全覆盖;随着气体的不断注入，半圆柱形气泡的高度进一步增加，形成槽道内较为严重的气泡阻塞现象，而且由于底部及侧壁上表面张力的作用，气泡由孔口脱离后是贴着槽道底面向下游滑动。0．032 s 时气泡出现明显缩颈，其后在剪应力及曳力作用下导致缩颈断裂，脱离孔口。气泡在逐渐排出槽道过程中，孔口处有新的气泡形成。当高宽比为2:1 时图3(b)，气泡从孔口逸出(0．001 s)、生长及脱离过程(0．016 s ～0．056 s)呈现出与高宽比为4∶1 时类似的规律，但可明显看出气泡的脱离时间较长，脱离体积更大;气泡脱离及贴着底面向下游滑动时(0．056 s、0．086 s)占据槽道的截面积增加，阻塞流道现象更加严重。当高宽比为1∶1 时图3(c)，气泡从孔口逸出后也会迅速向四周扩张(0．015 s)，但生长过程中在流体曳力和剪应力作用下，转而向下游延展;由于槽道宽度增加，气泡生长过程中仅能粘附至某一侧壁面(0．025 s ～0．04288 s)，在表面张力、绕流曳力和剪应力等共同作用下，由孔口脱离后向下游滑动并排出计算区域。当高宽比为1∶2 时图3(d)，气泡的整个生长、脱离及排出过程均未与两侧壁面发生接触;而且气泡从孔口逸出后，三相接触线没有呈现向四周扩张现象，而是向下游延展(0．013 s、0．025 s);另外从图中可以看出，气泡生长的最大高度较前述情况有所减小，气泡的脱离时间及脱离体积也较前三种情况有所减小(0．03516 s、0．046 s)。高宽比进一步减小至1∶4 时图3(e)，同样气泡从孔口逸出后三相接触线只是向下游扩张(0．001 s ～0．027 s);由于高度较小，气泡生长至脱离之前已与上壁面接触(0．027 s);一旦气泡接触上壁面，三相接触线即在上壁面迅速铺展开，在浮力和表面张力共同作用下，气泡产生震荡，导致气泡与孔口连接的颈部提前断裂(0．02967 s)，但气泡由孔口脱离后并未被液体快速带走，只以缓慢的速度向下游滑动;此时孔口又产生新的气泡，并快速生长(0．041 s)，与原脱离的气泡相接触、碰撞，发生两气泡聚合现象，形成的新气泡呈圆柱状，在液体曳力和剪应力作用下向下游运动并排出计算区域。随后孔口处下个气泡出现并重复这一过程。

图3 不同高宽比时槽道内气泡的生长脱离过程

表2 为矩形微槽高宽比对气泡脱离时间、脱离体积和排出时间的影响，其中排出时间定义为气体刚从孔口逸出到一个完整气泡被排出整个计算区域所需的时间。由表2 可知，气泡的脱离体积、脱离时间均随着槽道高宽比的减小呈现先增大，后减小的趋势;H/W=2 时，气泡的脱离时间最长，因此气泡的脱离体积也最大，排出时间也最长，说明处于该高宽比的矩形微槽内最不利于壁面逸出气泡的排除。H/W=0．25 时，气泡的脱离时间和脱离体积均小于H/W=0．5 时的情况，但气泡的排出时间却有所增加，主要原因是H/W=0．25 时，槽道高度较小，气泡生长至脱离之前已与上壁面接触，浮力的作用使气泡在上壁面的附着力加强，阻碍了气泡的排出，因此过小的高宽比反而不易于气泡的排除。

表2 矩形槽道高宽比对气泡脱离时间、脱离体积和排出时间的影响

图4 为高宽比对槽道底面气体覆盖率的影响。图中Ag为底面气体覆盖率，定义为底面气体三相接触线所围成的面积与槽道底面积之比;τ为量纲1 时间，是把气泡顶部从孔口刚刚冒出到脱离气泡移动到恰好要排出槽道的临界时间标准归一化而获得。由图中可知，H/W =4 和H/W =2 时的底面气体覆盖率基本一致，要大于H/W=1、0．5、0．25 时的气体覆盖率。这主要是因为在H/W=2 和H/W=4 这两种情况下气泡粘附了槽道两侧壁面，在槽道内以稳定半圆柱的形状存在，气泡绝大多数不发生或者仅仅发生少量形变，进而维持了较大的底面气体覆盖率。除此之外，由图还能看出随着高宽比的减小，底面气体覆盖率呈现出减小的趋势，其原因一是因为气泡的脱离体积减小，另一原因是由于槽道底面积的增大。

图4 高宽比对槽道底面气体覆盖率的影响

图5 中显示了高宽比对槽道内容积含气率的影响。图中Sg表示容积含气率，其定义为槽道内气体体积与整个槽道空间体积之比。由图中可以看出，H/W=2 时的容积含气率最大，其次为H/W =4 和H/W=1 时，然后是H/W =0．25 时，最后是H/W =0．5。这与表3 中矩形槽道高宽比对气泡排出时间的影响规律一致，导致该现象的原因也是类似的。

图6 显示了槽道高宽比对归一化流动阻力因子的影响。定义归一化流动阻力因子为f/fl，f 为气泡生长及脱离过程槽道内流体的流动阻力系数，反映

图5 高宽比对槽道容积含气率的影响

图6 槽道高宽比对归一化流动阻力因子的影响

由于气泡生长引起的流动阻力的变化，定义如下

式中

Δp——槽道进出口的压降大小;

ul、ρ——液体进口速度和液体密度;

L、DH——槽道的长度和当量直径;

fl——当槽道内没有气相仅有液相通过时的流动阻力系数。

由图可知，对所有测试工况，阻力系数f 均随气泡的生长和气体阻塞情况的愈加严重而增加，随气泡逐渐排出槽道而下降，气泡的存在导致流动阻力系数约增加1．4 ～2．1 倍。当H/W=1 时，阻力系数f 的变化最小，这是由于气泡此时只是粘附到槽道一侧壁面，对整个流道流通截面的阻塞并不严重，液体流动中所受局部阻力损失较小，因此归一化流动阻力因子在整个周期内变化较小。当H/W =2 时，归一化流动阻力因子的值最大，整个周期内的变化幅度也最大，主要原因是此时气泡的脱离时间和脱离体积较大，且粘附于两侧壁面，流道阻塞较严重。此外H/W =0．25 时在气泡生长脱离直至排出流道的一个周期内归一化流动阻力因子的变化幅度也较大，主要是气泡粘附了槽道顶部，使得难于排除，流道阻塞加剧所导致的。

3 结论

本文通过建立三维CFD 模型，结合VOF 方法，对不同流道结构下液体通流微小通道内壁面逸出气泡的形成、生长及脱离运动进行了数值模拟，讨论了槽道高宽比及槽道截面形状对气泡动力学行为的影响。主要结论如下:

(1)流道横截面积相同而高宽比不同时，气泡的脱离体积和脱离时间均随着槽道高宽比的减小呈现先增大，后减小的趋势。当高宽比为2 时，气泡的脱离体积、脱离时间、排除时间、槽道容积含气率和流动阻力因子均达到最大值。过小的高宽比(H/W=0．25 时)将导致气泡排出缓慢，流道内容积含气率和阻力系数反而增加。

(2)气泡的存在导致流动阻力系数约增加1．4 ～2．1 倍。

［1］Tadrist L． Review on two - phase flow instabilities in narrow spaces［J］．International Journal of Heat and Fluid Flow，2007，(28):54 -62．

［2］ 宗露香，徐进良，王晓东，等． 高热流作用下微通道内种子气泡热控沸腾传热数值模拟［J］． 机械工程学报，2013，49(14):125 -132．

［3］ Lutz Böhm，Tokihiro Kurita，et al． Rising behaviour of single bubbles in narrow rectangular channels in Newtonian and non-Newtonian liquids［J］． International Journal of Multiphase Flow． 2014(65):11 -23．

［4］ Shaodan Li，Sichao Tan，Chao Xu，et al． An experimental study of bubble sliding characteristics in narrow channel［J］． International Journal of Heat and Mass Transfer，2013(57):89 -99．

［5］ Jacqueline Barber，David Brutin，Khellil Sefiane，et al． Bubble confinement in flow boiling of FC-72 in a“rectangular”microchannel of high aspect ratio［J］． Experimental Thermal and Fluid Science，2010(34):1375 -1388．

［6］ Yang Z L，Dinh T N，Nourgaliev R R，et al． Numerical investigation of bubble growth and detachment by the Lattice - Boltzmann method［J］． International Journal of Heat and Mass Transfer，2001(44):195 -206．

［7］ Vafaei S，Angeli P，Wen D． Bubble growth rate from stainless steel substrate and needle nozzles［J］． Colloids and Surfaces A:Physiochemical and Engineering Aspects，2011(384):240 -247．

［8］ Akbar MK，Ghiaasiaan SM． Simulation of Taylor flow in capillaries based on the volume - of - fluid technique［J］． Industrial and Engineering Chemistry Research，2006，45(15):5396 -5403．

［9］ Chakraborty I，Biswas G，Ghoshdastidar P S． Bubble generation in quiescent and co-flowing liquids［J］． International Journal of Heat and Mass Transfer，2011(54):4673 -4688．

［10］ 谢建． 微小槽道内微孔壁面逸出气泡动力学行为及特性［D］．重庆:重庆大学，2013．