基于Kalman 滤波的ECT 图像重建算法*

李 佳，张立峰，田 沛

(华北电力大学 自动化系，河北 保定071003)

0 引 言

两相流或多相流广泛存在于化工、石油、电力等行业，精确检测出两相流或多相流的各相分布信息对生产过程的安全、经济、高效地运行具有重要意义。

电容层析成像(electrical capacitance tomography，ECT)技术基于电磁场敏感机理，利用重建算法实现对管道内部介质分布的二维或三维成像，在两相流或多相流的测量领域有一定应用［1～3］。使用ECT 技术在现场进行测量时，测量数据往往会携带噪声，降低了成像精度。本文对Kalman滤波的去噪效果进行研究，对三种流型在不同程度噪声下进行仿真，同时进行静态实验。

1 ECT 测量原理

ECT 利用管内不同相介质通常具有不同的介电常数，通过阵列电极的电容变化，反映管内相分布的变化，使用重建算法构造管道中的相分布图像。ECT 系统如图1 所示，主要由三部分构成:阵列电容传感器、数据采集系统和成像计算机。

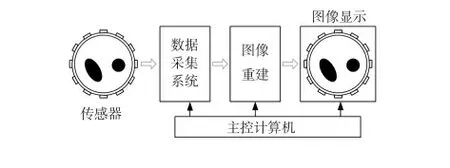
图1 12 电极ECT 系统结构图Fig 1 Structure chart of 12 electrodes-ECT system

ECT 系统通过均匀安装在绝缘管壁外的阵列电容传感器获得管内的物场信息，数据采集系统接收传感器的测量数据并传递给计算机，通过重建算法进行图像重建和显示。

由于ECT 为静电场模型，场域中不存在自由电荷，可以用麦克斯韦方程来表示［4］

式中 ε(x，y)为被测截面介电常数分布，E(x，y)为电场强度分布。将式(1)简化，并进行线性化可得到离散模型

式中 λ 为归一化后的电容值向量;G 为图像灰度值矩阵;S 为灵敏度矩阵;M 为独立测量数;N 为场域内剖分网格单元数。

2 基于Kalman 滤波的ECT 图像重建

Kalman 滤波是一种最优估计方法，以最小均方误差为估计准则，建立信号与噪声的状态空间模型，通过前一时刻的状态预测值和当前时刻的测量值来实现对当前时刻状态值的估计。为将Kalman 滤波应用到ECT 中，需要建立ECT 的状态空间模型。假设在测量电容值期间管内相分布不发生变化，即在图像重建过程中不考虑系统噪声，前一时刻的图像灰度等于当前时刻的图像灰度，则ECT 的状态方程为

式中 gk为k 时刻图像灰度，gk－1为k－1 时刻图像灰度。

由式(2)中图像灰度与电容值的关系建立测量方程为

式中 zk为k 时刻的归一化电容，S 为灵敏度矩阵，vk为k时刻的测量噪声，且噪声的协方差阵在实验中通常保持不变Rk=R，则ECT 系统的Kalman 滤波方程为［5～7］

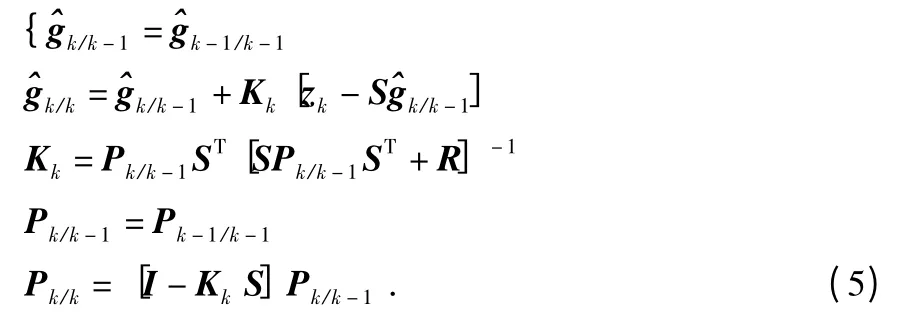
基于Kalman 滤波的ECT 图像重建有两个过程:预测和校正。预测过程估计当前图像灰度值和误差方差矩阵，作为下一时刻的先验估计信息;校正过程在先验估计的基础上，结合当前时刻电容值对先验估计值进行校正，得到最优图像灰度估计值，工作原理见图2。

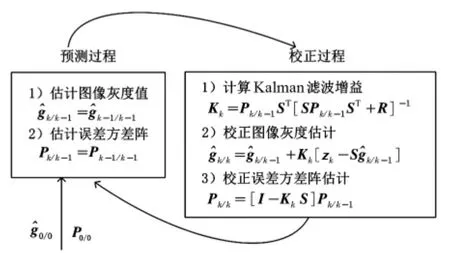
图2 基于Kalman 滤波的ECT 图像重建原理图Fig 2 ECT image reconstruction principle diagram based on Kalman filtering

3 仿真与实验结果

3.1 仿真结果

仿真环境:酷睿i5 1.7 GHz CPU，4 G 内存笔记本电脑。采用有限元方法求解ECT 正问题，并分别使用Kalman 滤波和Landweber 迭代进行图像重建，在Matlab 中编写软件包实现这些功能。采用的ECT 系统为12 电极，独立测量数66 个，管内剖分有限元网格768 个。

本文实验中得到的测量噪声协方差矩阵为R(方差数量级为－5)。为观察去噪效果，选取三种流型，分别向归一化电容值中加入均值为0，协方差矩阵为R，10R，100R的随机噪声，采用Kalman 滤波和Landweber 迭代进行图像重建。Kalman 滤波的灰度初始值取0，误差协方差矩阵初值取5×10kI66×66，其中，k 取对应噪声协方差矩阵数量级高2 个数量级，取迭代10 次时重建图像。Landweber 迭代灰度初始值取线性反投影(LBP)结果，迭代因子取1.5，取迭代100 次时重建图像，重建结果如图3 ～图5 所示。为定量比较重建图像的质量，采用图像相对误差(RE)作为评价参数［8］，且将计算得到的图像相对误差一并标注在图中。

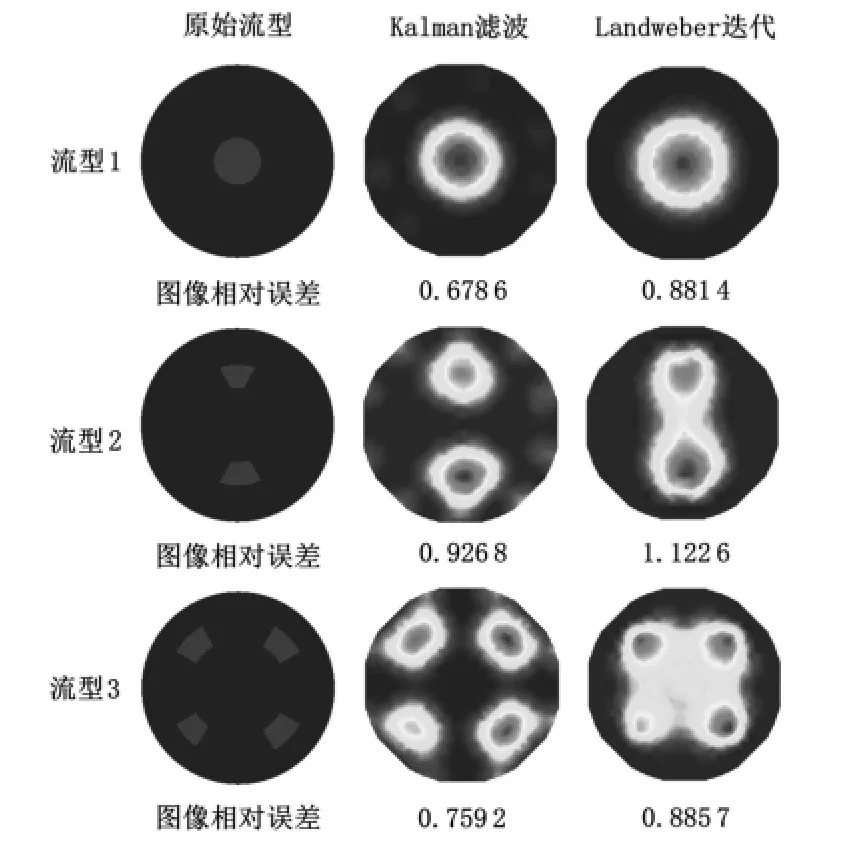
图3 测量噪声协方差矩阵为R 时重建图像Fig 3 Image reconstruction when the measurement noise covariance matrix is R

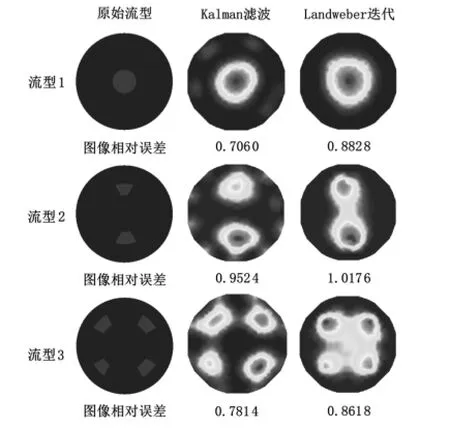
图4 测量噪声协方差矩阵为10R 时重建图像Fig 4 Reconstructed images when measurement noise covariance matrix is 10R

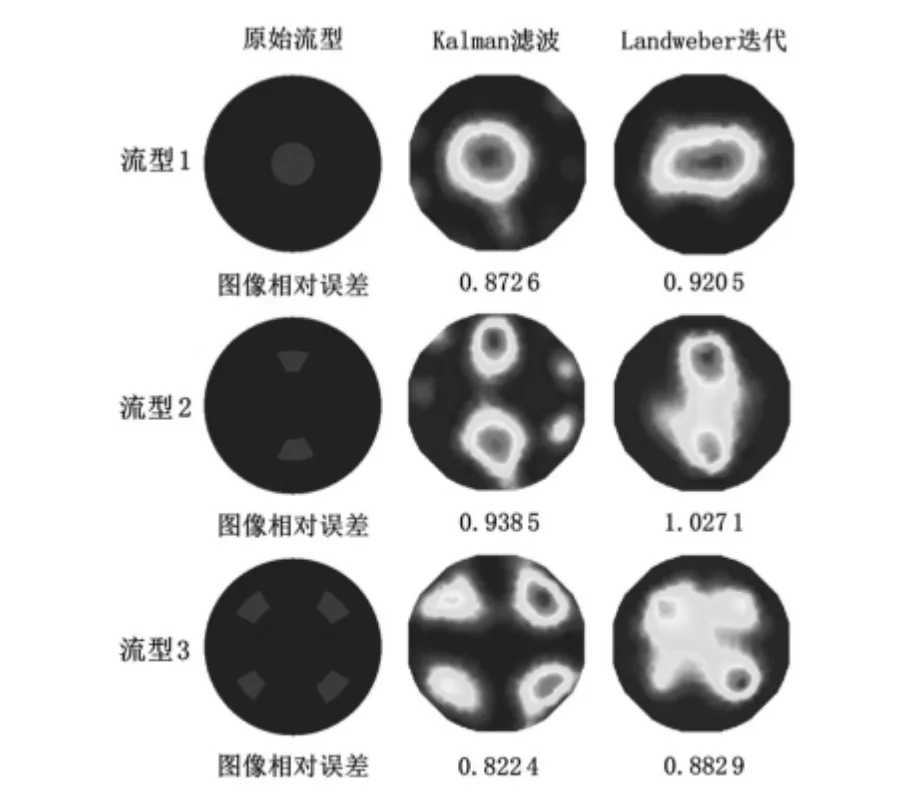
图5 测量噪声协方差矩阵为100R 时重建图像Fig 5 Reconstructed image when measurement noise covariance matrix is 100R

由图3 ～图5 可看出:在归一化电容值中添加噪声后，三种流型均为Kalman 滤波成像效果更好，相对应的图像相对误差更小。尤其当噪声协方差矩阵增加到100R 后，Landweber迭代算法重建结果中流型1 和流型3 出现严重失真，而Kalman 滤波仍可以重建出与原型较为接近的图像。

3.2 静态实验

静态实验采用天津大学研制的基于FPGA 的双模态(电容/电阻)成像系统，相关指标见文献［9］。Kalman 滤波初始灰度值取0，误差方差矩阵初值取5×10－3I66×66，取迭代10 次时重建图像，Landweber 算法初始灰度值取LBP结果，迭代因子取1.5，取迭代100 次时重建图像，如图6 所示。

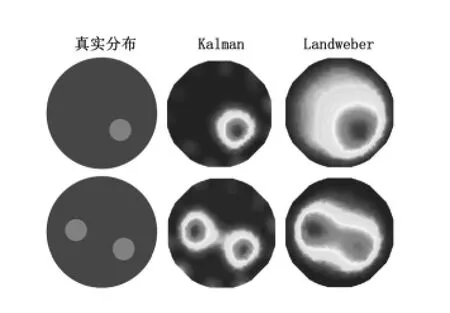
图6 静态实验结果Fig 6 Results of static experiment

第一种分布，一根有机玻璃棒靠近管壁，Landweber 算法成像伪影较大，Kalman滤波的重建图像边界清晰，圆度较好，大小更接近玻璃棒原型;第二种分布，两根有机玻璃棒都位于管壁与中心之间，Landweber 算法不能明显区分两棒，Kalman 滤波成像轮廓清晰，两棒之间有明显分割。

4 结 论

本文采用Kalman 滤波对ECT 进行图像重建，研究了Kalman 滤波算法的去噪效果。仿真与静态实验表明:与Landweber 算法相比，Kalman 滤波算法能够有效地降低噪声对测量值的影响，当噪声较小时，重建图像质量更高，相对误差更小;当噪声较大时，Kalman 滤波仍可以重建出与原型相近的图像，失真更小。

［1］ 郝魁红，范文茹，马 敏，等.平面式电容传感器阵列测量复合材料技术研究［J］.传感器与微系统，2014，33(2):35－38.

［2］ 马 敏，周苗苗，李新建.基于ECT 技术的航空发动机尾气监测系统设计［J］.传感器与微系统，2015，34(5):88－91.

［3］ 姜 凡，刘 靖，刘 石，等.电容层析成像技术应用于冰水两相测试研究［J］.中国电机工程学报，2010，30(5):49－53.

［4］ 王化祥.电学层析成像［M］.北京:科学出版社，2013.

［5］ Vauhkonen M，Karjalainen P A.A Kalman filter approach to track fast impedance changes in electrical impedance tomography［J］.IEEE Transactions on Bio-medical Engineering，1998，45(4):486－493.

［6］ Kim K Y，Kim B S，Kim M C，et al.Image reconstruction in time-varying electrical impedance tomography based on the extended Kalman filter［J］.Measurement Science＆Technology，2001，12(8):1032－1039.

［7］ 裴 珂，彭黎辉，张宝芬.基于Kalman 滤波的电容成像图像重建算法［J］.清华大学学报:自然科学版，2005，45(10):1332－1334，1351.

［8］ Yang W Q，Peng L H.Image reconstruction algorithms for electrical capacitance tomography［J］.Measurement Science ＆Technology，2003，14(1):R1－R13.

［9］ Zhang L F，Wang H X.Identification of oil-gas two-phase flow pattern based on SVM and electrical capacitance tomography technique［J］.Flow Measurement ＆ Instrumentation，2010，21(1):20－24.