基于齿侧间隙的非线性系统动力学建模及仿真

汪 雷，杨家军，胡 伟，邓家辉，黄 圣

(1 华中科技大学机械科学与工程学院，湖北 武汉 430074； 2 荆门楚大机电有限公司，湖北 荆门 448000)

仿真分析

基于齿侧间隙的非线性系统动力学建模及仿真

汪 雷1，杨家军1，胡 伟1，邓家辉2，黄 圣2

(1 华中科技大学机械科学与工程学院，湖北 武汉 430074； 2 荆门楚大机电有限公司，湖北 荆门 448000)

对单级斜齿轮传动机构进行了系统动力学建模与数值分析求解，针对齿侧间隙非线性问题采用连续的双曲正切函数来代替，把难于处理的非线性问题转换成线性问题。新的求解方法提高了数值稳定性，通过比较齿侧间隙对齿轮传动啮合力的影响，分析齿轮传动过程中外载下的位移响应曲线，为提高齿轮传动精度提供依据。

斜齿轮； 数值分析； 间隙非线性

斜齿轮作为机械传动中的一种常用减速机构，广泛应用于机械产品中。由于传动过程中啮合间隙的存在往往会产生振动噪声，影响传动精度，以往对间隙问题采用非线性分段函数表示，虽然可以表达间隙非线性问题，但是在数值求解过程中只有采用较小的步长来提高求解精度，不利于数值稳定性，对于复杂的问题增加了求解时间，而采用双曲正切函数来代替原分段间隙函数，能很好地解决上述的问题。本文最后给出了二级斜齿轮在给定齿侧间隙情况下的响应曲线，并比较了齿侧间隙对啮合力波动造成的影响。

1 齿侧间隙模型

齿轮的齿侧间隙是指相互啮合的齿轮齿面接触时，在非工作齿面之间形成的间隙。为补偿安装误差以及热变形，并保证齿轮的充分润滑，所有相互啮合的齿轮齿间必定存在空隙，。在齿轮的啮合过程中存在三种不同的啮合状态，分别为无冲击啮合、单边冲击啮合和双边冲击啮合[1]。

高速轴横向与轴向的啮合力

式中：βA为表示高速轴的啮合角；bA为高速轴啮合的齿侧间隙；f(z)，f(y)为表示横向与轴向的啮合力；同理可得低速轴的啮合力，只要把齿侧间隙换成相应的低速轴即可。

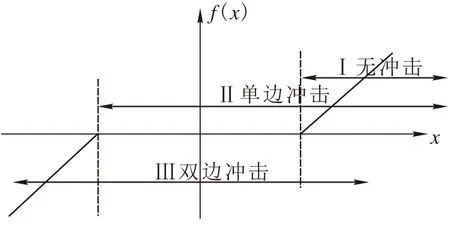
图 1 齿侧间隙模型

对于此类问题的处理，可以直接利用分段函数来代替齿轮的啮合间隙，但在数值仿真过程中会带来数值稳定性的问题，所以必须采用较小的步长来代替，但同时会增加问题求解的时间。为了解决这类问题，文献[2]提出利用多尺度法利用三次多项式来对间隙函数拟合。

为提高求解的精度，可将间隙拟合为七次多项式[2]。利用多项式对间隙函数进行啮合可以代替原来的分段函数，理论上多项式的阶次越高，拟合的精度就越高，但分析问题也会越来越困难，同时会带来多项式摆动问题。

因分段函数f是造成齿轮强非线性的主要因素之一，在求解过程中可以近似用一个连续函数代替，为了简化计算

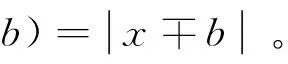
1)双曲正切函数[3]

g1(x)=xh(σx)；

(1)

2)反正切函数

(2)

式(1),(2)的逼近精度与正则化因子σ的选择有关：当σ取较小数值时，可以减少计算时间，提高结果的收敛性；相反，σ取的数值较大时，可与逼近的目标函数更好逼近；当σ取值非常大时候(如106)，逼近结果会非常好，但会影响数值的不稳定，尤其对于本文中的间隙非线性函数而言。当σ=200时，拟合精度达到计算的要求[3]。图2对间隙b取得0.1mm，对比以上2个函数与真实函数的啮合。

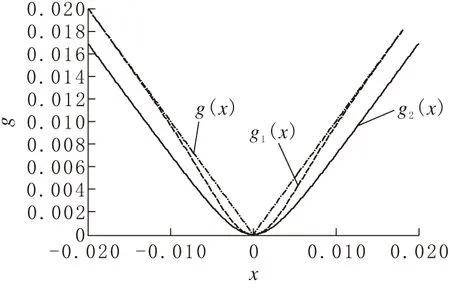
图 2 分段线性函数的近似平滑曲线

2 系统的动力学方程

不同于直齿轮，斜齿轮因啮合角的存在而会产生轴向力的分量。基于此，斜齿轮的振动产生不同于直齿轮的振动形态，即弯曲—扭转—摆动的耦合振动。而本文考虑高速级与低速级中间轴的扭转刚度与轴向刚度的影响，从而高速级与低速级又同时相互耦合，在此基础上建立了二级斜齿轮减速器的完全耦合模型。单级分析时忽略摩擦力等一些因素的影响，仅考虑轴承的支撑刚度与轴承阻尼的影响，以及传动轴的扭转变形、啮合阻尼、齿侧的间隙等影响。

每个齿轮在空间中有4个自由度，且沿着轴向的弯曲振动、扭转振动，沿着水平方向的扭摆振动、轴向振动(图3)。本文采用集中参数法对单级斜齿轮动力学建模，采用三维空间的动力学模型[4]，整体的自由度数为8个。

上式中的下标“1”、“2’分别代表齿轮1与齿轮2；字母“y”、“z”分别代表y，z轴的方向；ki(i=y,z)代表y，z方向的啮合刚度；ci(i=y,z)代表y，z方向的啮合阻尼；ci,j(i=1,2j=y,z)代表各轴承在y，z方向的支撑阻尼；ki,j(i=1,2j=y,z)代表轴承在y，z方向上的支撑刚度；mi,j(i=1,2j=y,z)为齿轮1，2沿着坐标轴方向上的平移质量；Ii,j(i=1,2j=y,z)为齿轮1、2在y，z方向上的转动惯量。T1d为输入轴的转矩。

yA(t)=y1+θ1zR-(y2+θ2zR2)

zA(t)=z1-(y1+θ1zR1)tanβ-z2

+(y2-θ2zR2)tanβ

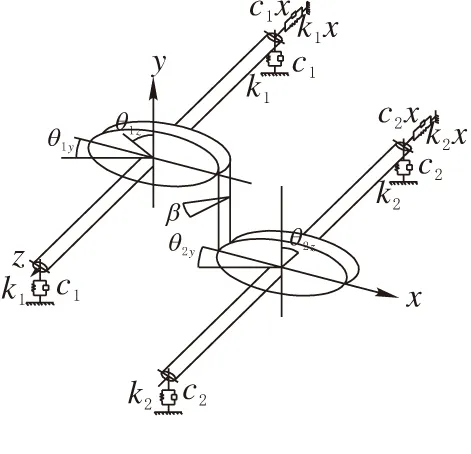
图 3 单级齿轮传动的原理图

2 仿真参数

2.1 驱动力矩与阻力矩

齿轮系统的名义功率为8kW；输入转矩为Td1(单位为N·m)，在正常状态下基本是恒定的，且

式中，n为高速级转速，1000r/min。阻力矩

z1,z2为主从动轮的齿数，分别为75，20。

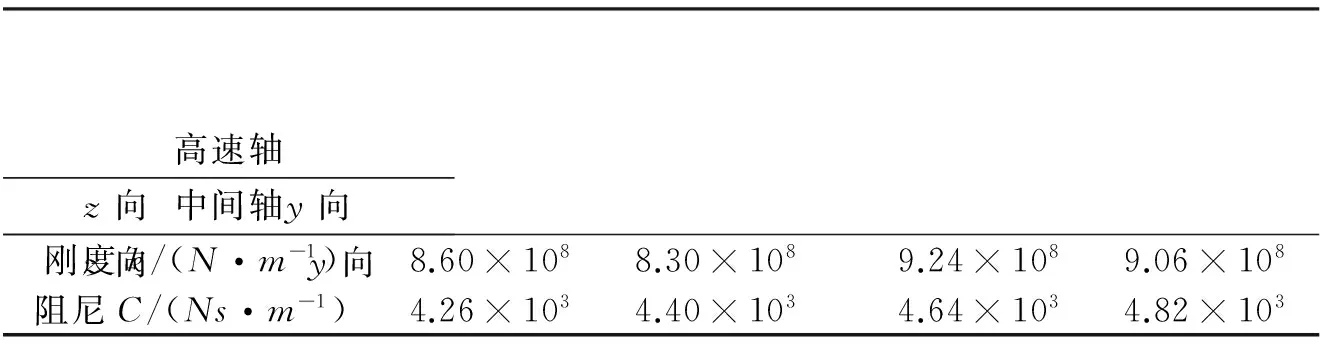
表1 轴系支撑轴承的刚度与阻尼值

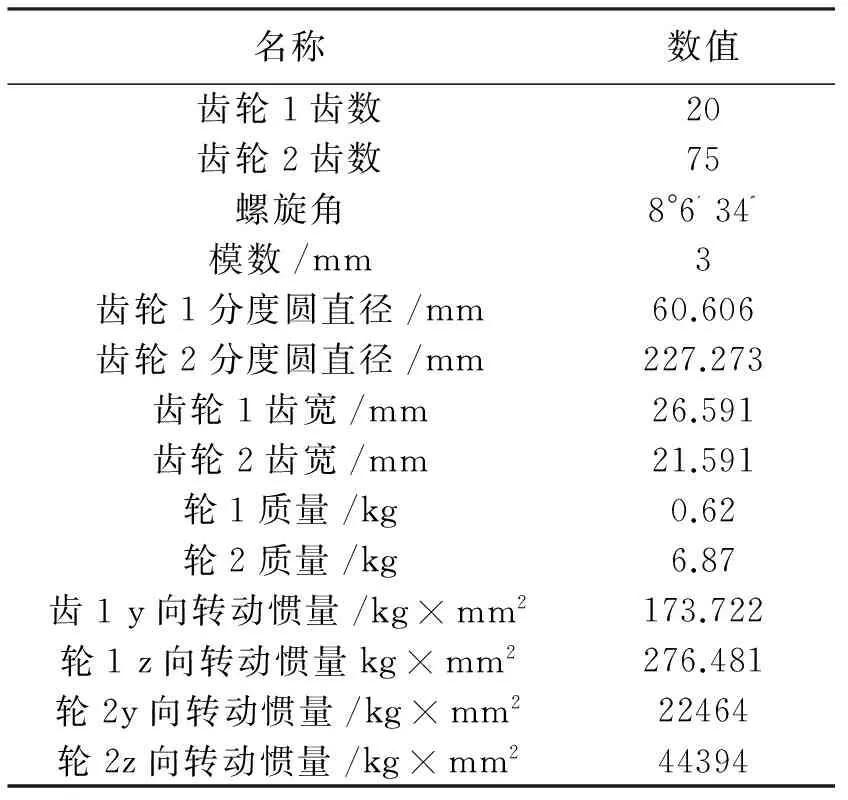
表 2 齿轮传动的尺寸参数

表3 啮合刚度与啮合阻尼

图 4 高速级齿轮1的y向振动位移曲线

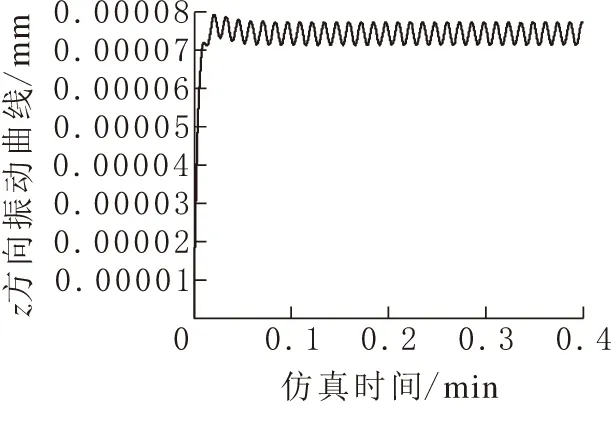
图 5 高速级齿轮1的z向振动曲线

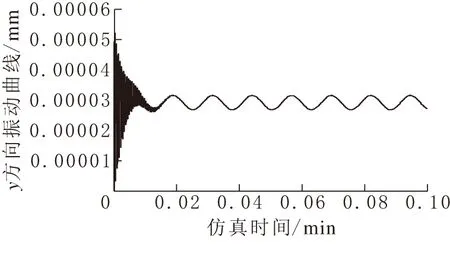
图 6 高速级齿轮2的y向振动位移曲线

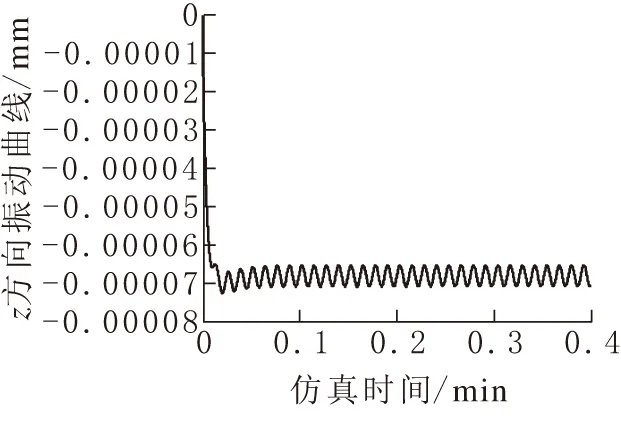
图 7 高速级齿轮2的z向振动曲线

上面的图形为对系统动力学方程利用simulink[5-6]进行了仿真分析的随着时间变化的仿真曲线，分别得到齿轮1,2沿着y,z方向振动的随时间变化的响应曲线，初始速度，初始位移全部选择为0，表示齿轮从启动到瞬态的情况，可以得到系统的瞬态响应。从仿真的结果可以看出来在仿真的开始出现较大的波动，之后得到一个规律波动的“稳态值”。此现象是由于系统的弹性支撑以及齿轮啮合的弹性变形引起的。

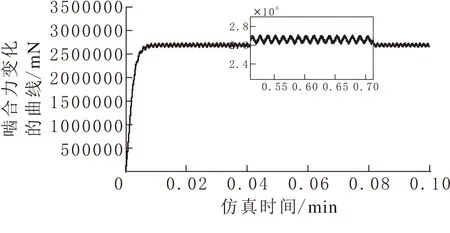
图 8 齿侧间隙影响下啮合力的变化曲线

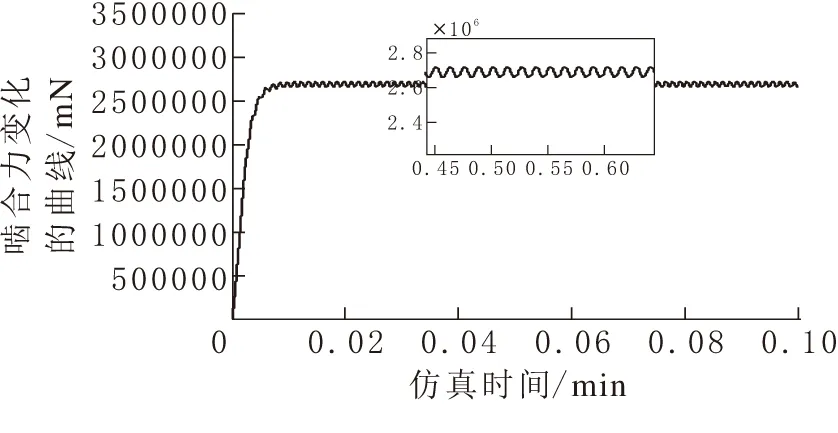
图 9 齿侧间隙为0时啮合力变化曲线

图8与图9对比了不考虑齿侧间隙情况下与齿侧间隙为2μm情况时的y向啮合力分量的变化曲线，从上面的曲线可以得出由于齿侧间隙的存在，在啮合过程中产生的冲击现象会带来啮合力的“毛刺”现象，会影响齿轮传动精度，这种情况在实际工作中可以通过提高齿轮制造精度与安装精度来避免。

4 结束语

本文采用simulink对单级斜齿轮传动系统进行数值仿真求解，对不容易处理的间隙非线性函数利用连续的双曲正切函数来代替，这样数值仿真上更加容易处理。虽然本文只是针对简单的单级间隙非线性传动系统的处理，这种方法同样适用于谐波齿轮传动，二级斜齿轮等传动系统，为齿侧间隙分析提供了一种有效方法。

[1] 王建军,李润方. 齿轮系统动力学：振动、冲击、噪声[M].第一版.北京: 科学出版社,1997.

[2] 李文良. 计及齿面摩擦的斜齿轮传动动态特性研究[D].哈尔滨： 哈尔滨工业大学，2013.

[3]KimTC,RookTE,SinghR.Effectofsmootheningfunctionsonthefrequencyresponseofanoscillatorwithclearancenon-linearity[J].JournalofSoundandVibration, 2003, 263(03): 665-678.

[4] 王 庆. 齿轮系统的动态设计[M].北京：气象出版社, 2014.

[5]KarrisST.Introductiontosimulinkwithengineeringapplication[M].OrchardPublications,2010.

[6] 张志涌. 精通matlabR2011a[M].第二版. 北京：北京航空航天大学出版社,2011.

[责任编校： 张 众]

Modeling and Simulation of Gear System based on the Nonlinear Clearance

WANG Lei1,YANG Jiajun1, HU Wei1, DENG Jiahui2, HUANG Sheng2

(SchoolofMechanicalSci.andEngin.,HuazhongUniv.ofSci.andTech.,Wuhan430074,China)

This article carried out the system dynamics modeling and numerical solution for single-stage helical gear transmission mechanism. Continuous hyperbolic tangent function was used for the backlash nonlinear problem; the difficulty of nonlinear problem was transformed into a linear problem. This new method improves the numerical stability, through comparing the influence of the backlash on the gear meshing force and analyzing the displacement response curve so as to provide the basis for improving the accuracy of gear transmission.

helical gear; numerical analysis; clearance of nonlinear

2015-04-20

汪 雷(1987-)，男，吉林四平人，华中科技大学硕士研究生，研究方向为机械振动，机械结构的动态设计与

1003-4684(2015)04-0061-04

TH132.413

A