基于子模型算法的某螺旋桨遥测盘局部强度计算与分析

，，，

(1.中国飞行试验研究院，陕西 西安 710089；2.中航工业惠阳航空螺旋桨有限责任公司，河北 保定 071000)

0 引言

在有限元计算中，经常会由于模型复杂、网格数量巨大，导致计算不收敛、精度低等问题。尤其对应力集中部位的计算结果有严重影响[1,2]。而这些部位往往是危险点，对结构的强度评价起关键作用[3]。针对这类问题，有限元理论中提出了一种高级分析方法——子模型算法(Submodeling)，尤其适用于小曲率圆角、圆孔方孔、复杂过渡截面等细节的计算分析[4]。子模型算法具有计算耗时短、网格质量高、应力梯度小等特点。本文以某螺旋桨遥测盘为研究对象，通过子模型算法对遥测盘的局部强度进行数值模拟，考核遥测盘的局部强度，并对计算方法进行总结。

1 子模型算法简介

子模型算法的基本术语有：全局模型、子模型、子模型边界及驱动变量。全局模型即为分析结构的全局模型。对全局模型中所关心的部分进行切割所建立的模型为子模型。切割的边界成为子模型边界，是子模型与全局模型的交界面或曲线。驱动变量是子模型从全局模型中继承的结果变量[5]。

子模型算法的思路是在全局模型计算结果的基础上，截取全局模型的一部分建立子模型。子模型通常更接近真实几何结构，具有更高的网格质量，并与全局模型具有相同的材料属性，单元类型可以不同。结构静力分析中的驱动变量一般是位移，通过形函数插值，可以将全局模型的位移结果传递给子模型，作为初始位移边界条件。对子模型进行分析，可以得到关注区域的更高精度解。

子模型算法的理论基础是圣维南原理，即当作用在弹性体上的一个力被另一个静力等效的力所替代时，只有在力的作用区域附近，才会引起应力分布的变化，在远离作用区域的地方，应力的分布没有变化。子模型算法的精髓在于将除了子模型之外的全局模型用静力等效的边界位移场来代替，极大地缩减了计算模型的规模。计算结果对于子模型边界的选取有一定的敏感性，因此应使边界远离应力集中和高应力梯度区域，才能使子模型对集中区域的表征不受边界截取方式的影响。

2 全局模型分析

航空动力装置上的大型旋转部件通常为循环对称构型，结构复杂，工作在高转速和恶劣的振动环境下。某螺旋桨遥测盘主要功能是实现螺旋桨应力的非接触测量，遥测盘为3扇区周向循环对称结构，每个扇区上设计有发射机、航空插头和电池安装座，在盘外缘安装有桨帽，遥测盘和桨帽材料参数见表1。取遥测盘和桨帽的1/3模型导入有限元软件ANSYS，划分扇区时尽量保证不切割遥测盘上的电池、模块安装座等复杂截面。选用二阶四面体单元SOLID92进行网格自动划分，对遥测盘和桨帽接触部分采用共节点处理以实现边界的力传递。网格模型如图1所示，包含181560个网格，346744个节点。

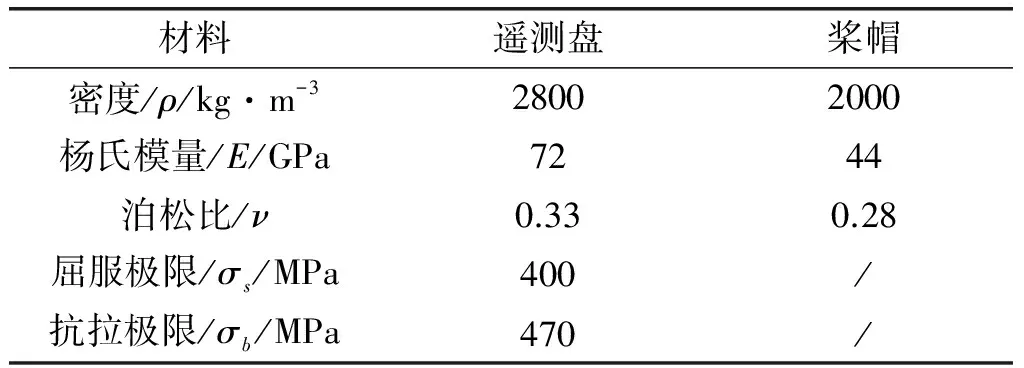
表1 遥测盘材料参数

根据遥测盘的安装和工作情况，需要考虑以下边界条件：

1)对于1/3扇区需施加循环对称边界条件；

2)遥测盘通过内侧12个孔安装在桨轴上，在安装孔处施加位移约束；

3)遥测盘工作时承受自身离心载荷作用，施加全局角速度；

4)在遥测盘内安装的发射机模块和电池对盘产生离心力，通过压力施加在作用面；

5)在盘外缘安装有电源开关，产生的离心力通过集中力施加在作用点。

遥测盘上的边界条件见图2。

在100%转速下对全模型进行了求解，应力分布如图3所示。最大Von-Mises等效应力为65.74 MPa，出现在电池安装座的底部。该区域存在明显的应力集中，在网格较粗的情况下，得到的结果存在应力平均效应，应重点考虑这一区域。另外，图中右侧外缘处的应力也较大，此处安装了电源开关，开关的模型细节较为复杂，全局模型边界条件5)将开关对盘的作用简化为集中力并不准确，因此开关部分也需要进一步计算。

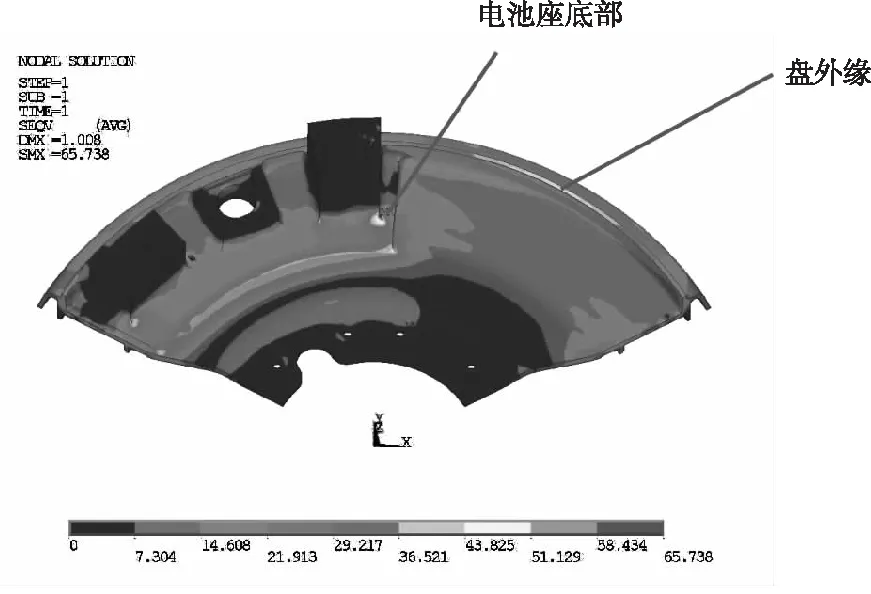
图3 100%转速遥测盘应力云图

3 子模型分析与验证

图4 子模型边界划分

根据第3节的应力分析结果，分别建立电池安装座和电源开关部分的子模型，如图4所示。其中电源开关子模型在开关区域进行了进一步的网格细化。

从全局模型结果文件中提取子模型边界部分的位移场，并进行线性插值。对于10节点四面体单元SOLID92，传递函数为：

u=Niui+Njuj+Nkuk+Nlul+Nmum+Nnun+Nouo+Npup+Nquq+Nrur

v=Nivi+Njvj+Nkvk+Nlvl+Nmvm+Nnvn+Novo+Npvp+Nqvq+Nrvr

w=Niwi+Njwj+Nkwk+Nlwl+Nmwm+Nnwn+Nowo+Npwp+Nqwq+Nrwr

(1)

其中u，v，w为子模型节点初始位移，us，vs，ws(s=i，j，…r)为该节点所处的全局模型单元10个节点的位移，Ns(s=i，j，…r)为单元形函数。

子模型除了位移继承于全局模型之外，其他边界条件如压力、体积力等与全局模型保持一致。分别对上述两个子模型施加边界条件，进入求解器求解，提取Von-Mises等效应力结果绘制云图，见图5。可见子模型的应力分布趋势与全局模型相同。在图5(a)中，最大应力仍出现在安装座底部，但数值从65.74 MPa变为77.21 MPa，增长了17.4%。在图5(b)中，最大应力出现在盘外缘根部的凸台处，主要是由于开关的离心效应，对这一区域产生了弯矩。最大应力为46.50 MPa。

图5 子模型Von-Mises等效应力分布

在对子模型进行计算之后，首先要验证子模型对全局模型结果的继承性，保证子模型的位移边界是准确可靠的。在遥测盘直径466 mm位置取一条环形路径，分别提取全局模型和上述两个子模型沿路径的位移，如图6所示，图中虚线为全局模型，实线为子模型，横轴为路径距离。

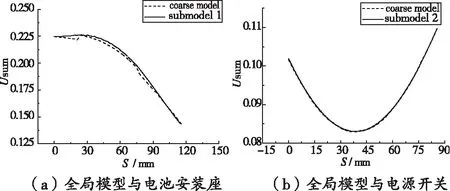
图6 路径位移对比

在路径起始和结束位置子模型与全局模型位移数据完全重合，在其他位置也具有相同变化趋势，跟随度较好。并且子模型位移曲线更为平滑，这是由于子模型网格致密，位移场的连续性更好。因此认为子模型对全局模型继承性良好，计算结果准确。

4 强度校核

引入设计安全系数和许用安全系数对盘的旋转强度进行评价。用材料允许的极限应力除以机械零部件中的实际最大应力，得到的系数为设计安全系数[6]。此处遥测盘材料的屈服极限σs=400 MPa作为极限应力，即：

ns=σs/σmax

(2)

根据螺旋桨部件的设计要求，遥测盘的许用安全系数[n]应在2以上，得到遥测盘的强度判据为：

ns≥[n]=2

(3)

强度校核结果见表2，在100%转速下，盘上的最大应力为电池安装座底部的77.21 MPa，最小设计安全系数为5.18，表明遥测盘的强度满足要求，强度设计具有较高的裕度。

表2 强度校核结果

5 结论

本文介绍了有限元子模型算法的基本原理，对某螺旋桨遥测盘进行了局部应力计算，并进行了强度校核，得到如下结论：

1)遥测盘各危险部位的强度设计满足要求；

2)当三维模型所关心部位的细节较为复杂时，有限元建模应尽量少作简化，使用子模型算法分析细节部位可以达到可靠的精度；

3)循环对称扇区划分应尽量使高应力区远离循环对称边界，避免在后续分析中跨循环对称边界建立子模型，造成子模型的不连续性。

[1] A.E. Bogdanovich;I.Kizhakkethara. Three-dimensional finite element analysis of double-lap composite adhesive bonded joint using submodeling approach[J].Composites. B, Engineering, 1999(6)537-551

[2] Hao Wang, Aiqun Li, Ruomei Hu, Jian Li. Accurate stress analysis on steel box girder of long span suspension bridges based on multi-scale submodeling method[J]. Advances in structural engineering,2010(4)727-740

[3] Mitsuru Kitamura, Hideomi Ohtsubo, Akira Akiyama, Hiroki Bandoh. Submodeling analysis of Ship structure with superconvergent patch recovery method[J]. International Journal of Offshore and Polar Engineers, 2003(3)216-223

[4] 张朝晖.ANSYS11.0结构分析工程应用实例解析[M].北京：机械工业出版社，2007

[5] 刘保林. 基于有限元子模型的曲轴强度及耐久性分析[J]. 柴油机设计与制造, 2011, 17(3):17-20

[6] 秦大同,谢里阳.机械设计手册[M].北京：化学工业出版社，2011