基于正定矩阵等价性的判定方法

张二喜，杨 浩，刘高杰

(成都理工大学管理科学学院，四川 成都 610059)

基于正定矩阵等价性的判定方法

张二喜，杨 浩，刘高杰

(成都理工大学管理科学学院，四川 成都 610059)

运用高等代数中一系列矩阵理论的相关知识，讨论了正定矩阵的等价条件，通过这些等价条件得到了正定矩阵的若干判定方法，如定义法、顺序主子式法、合同关系法、特征值法以及半正定法，并对每一种方法做了实例说明.

正定矩阵;等价条件;判定;顺序主子式;合同;特征值;半正定

0 引言

随着数学本身及应用矩阵的其它学科或领域的发展，正定矩阵引起了国内外学者的广泛关注［1－4］.对正定矩阵判定的研究也取得了巨大进展［5－8］.二次齐次多项式在实际工作和理论研究中是一种重要的多项式，它不仅在数学的许多分支中要用到，而且在物理学中也会经常遇到.实二次型的正定二次型具有特殊的位置，正定二次型的系数矩阵就是正定矩阵.因此，对正定矩阵的讨论研究无论在矩阵理论方面，还是实际应用方面都有重要的意义.本研究在前人的基础上对正定矩阵的性质、判定做了进一步的讨论研究，获得了相应的一些结论.

1 正定矩阵的等价条件

1.1 正定矩阵的定义

定义1［1］n阶实对称矩阵A称为正定矩阵，如果对于任意的n维实非零实列向量X，都有XTAX＞0.正定的实对称矩阵A简称为正定矩阵，记作A＞0.单位矩阵E就是正定矩阵.

1.2 正定矩阵的等价条件

定理1 设A为n阶实对称矩阵，则以下条件等价［2－3］:

1)A为正定矩阵;

2)对于任意一组不全为零的数 c1，c2，…，cn，有，

3)任意 α ∈Rn，α ≠0，有，α'Aα ＞ 0;

4)任意n阶可逆阵C，C'AC正定;

6)存在正交阵P，使P'AP=In;

7)A的特征值全大于0;

8)A的顺序主子式全大于0.

2 正定矩阵的判定方法

2.1 定义法

运用正定矩阵的定义来判定正定矩阵有时很简便.

例1 如果A，B都是n阶正定矩阵，证明，A+B也是正定矩阵.

证明 因为 A，B为正定矩阵，所以 X'AX，X'BX为正定二次型，且

因此，

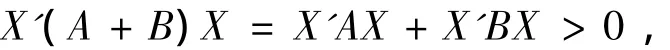
于是，X'(A+B)X必为正定二次型，从而A+B为正定矩阵.

2.2 顺序主子式法

在上述等价条件中，条件1)与8)是等价的，因此可借助顺序主子式来判定正定矩阵，即n阶实对称矩阵A的一切顺序主子式都大于0，则A为正定矩阵［4］.

解 二次型f的矩阵为三角矩阵，

A的任意的k阶顺序主子式，

所以，矩阵A为正定矩阵，原二次型为正定二次型.

2.3 合同关系法

例3 A合同于n阶单位矩阵E，则A为正定矩阵.

证明 若A合同于E，则存在可逆矩阵B，使得，

任取，X≠0，BX=Y=(y1，y2，…，yn)T，则Y≠0.

于是，

故A为正定矩阵.

2.4 特征值法

在等价条件的讨论中，条件1)等价于7)，因此可借助特征值来判定正定矩阵，即n阶实对称矩阵A的所有特征值都大于0，则A为正定矩阵［8］.

例4 试证二次型，

为正定二次型.

证明 设f对应的矩阵为A，则，

计算可得，

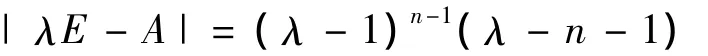
所以，A 的特征值为，λ1= … = λn－1=1，λn=n+1，由于A的特征值全为正，所以A为正定阵，从而f为正定二次型.

2.5 半正定法

例5 设A是n阶正定矩阵，B是n阶半正定矩阵，求证，

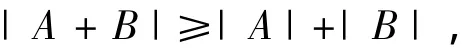
当且仅当B=0或n=1时等号成立.

证明 由A＞0知，存在n阶可逆矩阵P，使得PTBP=En，有，

又因为PTBP显然是半正定的，设，

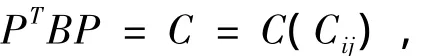
则有，

其中，ci是 C 的所有 i阶主子式之和，i=1，2，…，n.因为，C=PTBP≥0，它的主子式都非负，因此，

所以，

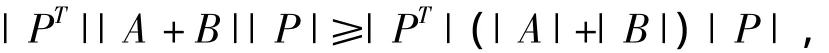
由此得，

当B=0或n=1时，显然，

成立.

当 B≠0且n ＞1时易知PTBP=C≠0n×n，于是至少有一个cij≠0，此时C的一阶主子式cii，cjj不能为零，否则，这与C半正定矛盾.于是c1＞0，进一步有，

从而，

成立.

［1］王萼芳，石生明.高等代数［M］.北京:高等教育出版社，1996.

［2］张奎，杨侠.正定矩阵的若干等价条件［J］.阜阳师范学院学报(自然科学版)，2005，22(1):19 －20.

［3］王平.广义Fuzzy正交矩阵［J］.四川师范大学学报(自然科学版)，2003，26(4):366 －369.

［4］司凤娟.实正交矩阵的性质及判定［J］.科技视界，2013，3(17):85.

［5］姜国.正定矩阵的判定与性质［J］.湖北师范学院学报，2006，26(1):15 －16.

［6］倪凌炜.实正定矩阵的若干判定方法［J］.湖州师范学院学报，2004，26(2):12 －14.

［7］胡跃进，骈俊生.广义正定矩阵的一个不等式［J］.阜阳师范学院学报，2001，18(1):10 －11.

［8］陈惠汝，刘红超.关于正规矩阵的判定［J］.高师理科学刊，2009，29(5):87 －89.

Determination Method Based on Equivalence of Positive Definite Matrix

ZHANG Erxi，YANG Hao，LIU Gaojie
(College of Management Science，Chengdu University of Technology，Chengdu 610059，China)

This paper uses a series of advanced algebra matrix theories to discuss the equivalence conditions of positive definite matrix.By these conditions，we obtain several determination methods for positive definite matrix，including the definition method，the order principal minors method，the contractual relationship method，the eigenvalue method and the positive semi-definite method.This paper gives one example for each method.

positive definite matrix;equivalence condition;determination;order principal minors;contract;eigenvalue;positive semi-definite

O151.21

A

1004－5422(2015)01－0032－03

2015－02－04.

张二喜(1990—)，男，硕士研究生，从事概率论与拓扑学研究.

book=218,ebook=218