红外热波无损检测图像噪声分析与抑制

王冬冬，田 干，杨正伟，陶胜杰，张 炜

(第二炮兵工程大学，陕西 西安710025)

1 引言

红外热波无损检测是一种新型的无损检测技术，该方法通过对被检测对象施加主动的热激励(如高能脉冲闪光灯激励、超声热激励等)，然后通过红外热像仪采集试件表面的温度变化信息，将结构中的损伤或缺陷信息通过热图序列的形式表现出来。该方法因其速度快、非接触、直观显示、能够在线在役检测等优点，获得了广泛的应用。然而从试验中获取的原始热图序列，因为试件表面不均匀、红外热像仪的成像探测器及环境等因素的影响使得原始热图中存在强烈的噪声，降低了热波图像的质量［1］，严重影响后续对结构中损伤或缺陷的定量分析。因此，对红外热波检测图像中噪声的分析和处理，以增强图像对比度就成了红外热波检测技术的重要研究内容。

目前，对红外热波图像的去噪增强处理已有大量的研究［1－6］。除将传统机器视觉中的相关方法引入到热波图像处理中，还针对热波图像的特点发展了相应的去噪增强算法。本文针对获取的红外热波原始图像中存在的高噪声、低对比度等问题，为了改善热波图像的噪声抑制效果，在分析热波图像中噪声的基础上，将偏微分方程方法引入到热波图像的去噪处理中。偏微分方程方法因具有高度的灵活性及较强的局部自适应性［7］，能够在去除图像噪声的同时，有效地保持图像中非噪声信号的细节［8］，显著提高图像中目标与背景的对比度。相应的试验结果表明:无论是从视觉效果还是客观的评价指标，本文所提出的算法均具有较好的噪声抑制效果。

2 热波检测图像噪声分析

热波检测技术获得的图像代表了被检测对象表面温度分布信息，这为后续对被测对象进行损伤识别与评估提供了重要的信息。但是热波成像的机理决定了热波图像的信噪比、灰度及纹理等信息，使得获取的热波图像质量受到一定的影响。如果在原始热图上对结构中的损伤进行提取和识别，将严重影响识别的精度和准确性，对损伤的预测和评估产生严重的干扰。因此，在对后续研究进行之前必须对获得的热图中的噪声进行分析和处理，以保证后续研究内容的精度和准确性。热波检测技术的原理如图1所示。

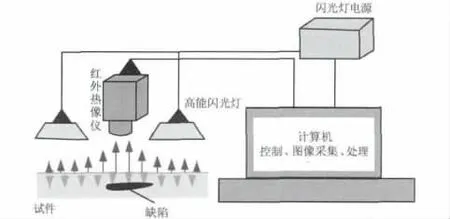
图1 热波检测技术的基本原理Fig.1 Fundamental principle of infrared thermography

从上述热波检测技术获取热图的过程中可知，热图中的噪声主要来源于被测结构表面情况的干扰、环境干扰及热像仪获取图像的过程中。红外热波图像反映的是被测对象中损伤区域与完好区域向外界发射红外辐射能量之间的差异。因此，被检测对象表面的特性(包括表面的光洁度及颜色等)将引起被测对象在主动加热过程中对热量的吸收不等，从而导致物体向外的红外辐射能力不同，造成获取的热波图像中存在一定的噪声干扰;在试验过程中，环境温湿度、操作人员的相关操作动作等都将引起一定的干扰量，从而导致采集到的热波图像中存在相应的干扰量，引起图像质量的下降;试验过程中采用的红外热像仪与普通的可见光成像设备不同，红外成像元件存在光敏响应非均匀的特点［9］，特别是个别的光敏元件还存在哑元的可能，因此，红外热像仪采集到的热波图像存在多种复杂的噪声干扰。

从上述的分析可以看出，热图序列中的噪声在图像采集的过程中是不可避免的，噪声的存在严重降低了热图像的可视性和质量，因此，必须对获取的热图像进行去噪增强处理，以提高图像中损伤区域与背景区域的对比度，为损伤的提取和识别奠定基础。

3 偏微分方程用于图像去噪的理论基础

偏微分方程方法用于图像处理的研究是从高斯滤波器引入的［10］。相关的研究表明多数的局部滤波器在使用时均可以转换为相应的微分算子进行运算，对于微分方程在图像处理中的应用来说，应用最为广泛的是热扩散方程。其相应的物理模型为:一个局部被加热的物体，随着加热过程的持续，物体本身吸收到的热量会慢慢扩散，直至整个物体的温度达到一致。将该模型应用到图像去噪过程中，就好比将图像中的噪声进行扩散使整个图像的灰度达到一致［11］，从而使图像中的噪声得以消除。

利用I(x，y)表示待处理的原始图像，I(x，y，t)表示时间t时刻的扩散图像，忽略计算过程中无关紧要的常数，可得图像的线性扩散偏微分方程为［7］:

Gtx，( )y表示中心在坐标原点的二维高斯函数。从上述的分析可见，对图像进行扩散即为计算原始图像与高斯函数的卷积，实际上就是采用传统的高斯滤波器对图像进行滤波处理。

4 基于改进的非线性扩散偏微分方程的热波检测图像去噪增强

在使用热扩散偏微分方程对图像进行处理时，是沿着图像中所有的方向进行滤波的，因此在平滑图像的同时，也破坏了图像中边缘等细节信息［12］。为了同时达到去除噪声并保护边缘等细节信息的目的，应该根据图像的内容在扩散过程中采用不同的“热扩散系数”，具体来说，就是将平滑的强度在边缘的位置减弱，在非边缘区域增强;在平行于边缘的方向进行平滑而在垂直于边缘的方向不进行平滑，从而实现在去除噪声的同时较好的保持图像中的边缘的细节信息［13］。为了实现上述目标，Perona和Malik于1990年对热扩散方程进行了改进，引入一个具有单调递减的非负函数g(r)，将由热扩散方程推导得到的线性扩散偏微分方程(1)修改为:

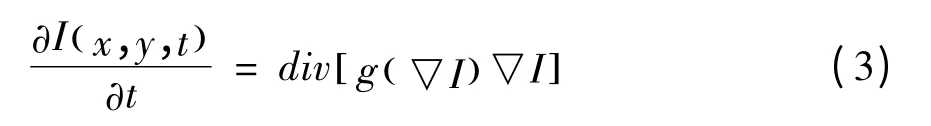
公式(3)通常被称为P－M方程，其中g(r)称为边缘停止函数，简称为边缘函数。公式(3)中的“热扩散系数”依赖于演化过程中的图像I(x，y，t)，因此P－M方程属于非线性扩散偏微分方程［14］。

在实际图像去噪增强的应用中，图像的边缘信息无法预先得到，因此就需要构造出一个边缘函数作为边缘点的估计，常用的边缘函数为:

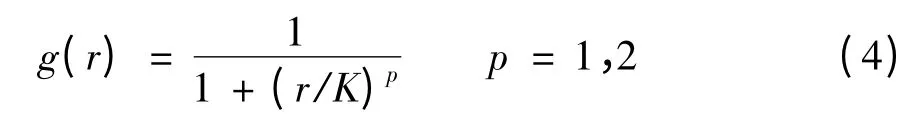
式中，K是常数，它可控制边缘函数的下降速率。

在P－M方程中，常用的两种边缘函数为:

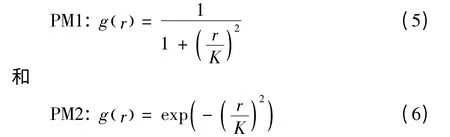
在上述方程中，边缘函数的值越大扩散性越强，合适的K值能够起到增强图像边缘的效果。公式(5)和公式(6)的取值范围为［0，1］。在P－M方程中的两种边缘函数均是图像梯度的函数，随着图像梯度的增加而单调下降。该方程虽然在抑制图像噪声和增强图像边缘方面有了一定的改进，但当被处理图像中的噪声程度较为强烈或图像的对比度较低时，图像的梯度震荡较大，导致对图像的去噪增强效果较差。为了解决这一问题，必须重新构造新的边缘函数。

［14］的基础上，对非线性扩散偏微分方程的边缘函数进行如下改进:

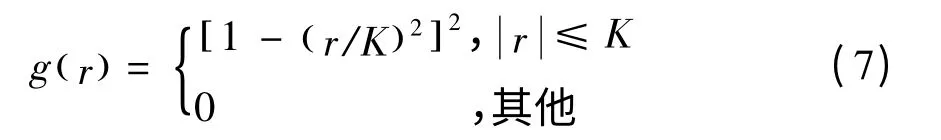
根据公式(7)，针对不同的K值(分别取值为K=10，20，50)画出边缘函数与图像梯度的关系如图2所示。

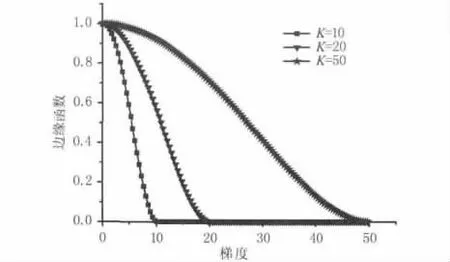
图2 边缘函数与图像梯度之间的关系Fig.2 The relationship between edge function and image gradient

从图2边缘函数与图像梯度的关系可知，当梯度值较小时，图像的扩散幅度较大，可以快速地滤除图像中的噪声;随着梯度值的增加，扩散幅度逐渐减小，知道边缘函数取值为0，这种趋势能够很好地保留图像中的边缘等细节信息。为了改善本方法在图像去噪增强中的实际应用效果，可以根据具体的被处理对象，选用合适的常数K来控制边缘函数的下降速率，从而取得较好的图像去噪效果。

从上述的理论分析，可得改进后方法在图像去噪处理中应用流程如图3所示。

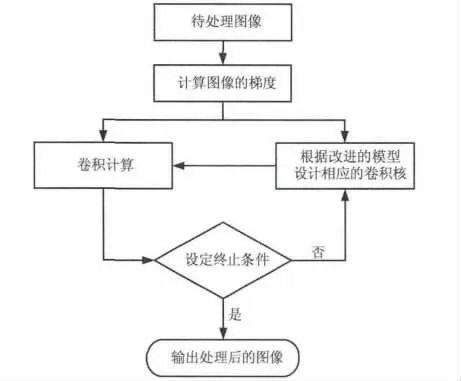
图3 文中方法在图像去噪应用中的流程图Fig.3 The flow chart of this method in image denoising

5 试验及结果分析

5.1 试验概述

针对复合材料脱粘损伤试件(如图4所示)，采用课题组自主研发的脉冲红外热波检测系统对试件进行检测研究。检测系统中脉冲红外热像仪采用德国InfraTec公司生产的Vhr 680非制冷性红外热像仪，其光谱响应范围为7.4～14μm，可提供640×480像素的热图像，热灵敏度为0.04℃(30℃);脉冲激励装置由两个高能氙灯提供，每个灯的最大激励能量为4.8 kJ，激励脉冲宽度为0.2 ms。通过实验得到的原始热图如图5所示。

图4 试件图Fig.4 Test specimen photo

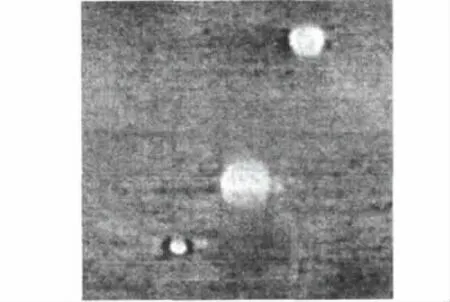
图5 热波检测原始热图Fig.5 Original thermal image of thermal wave testing

试件厚度为5 mm，其中预埋了三个利用聚四氟乙烯模拟的脱粘缺陷，从得到的热图中可以观察到三个亮斑，其分别对应预埋的三个缺陷。但是原始热图中存在的噪声等干扰，降低了热图的对比度。

5.2 结果处理分析

对试验中获取的原始热图采用上述提出的改进算法进行去噪增强处理，并将处理结果与低通滤波及传统的两种P－M边缘函数的处理结果进行对比，得到的三种偏微分方程方法的边缘函数曲线如图6所示，相关热图的去噪处理结果如图7所示。

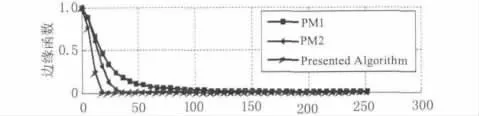
图6 边缘函数与图像梯度的关系(K=16)Fig.6 The relationship between edge function and image gradient(K=16)

从图7的处理结果中可以看出，经过改进的非线性偏微分方程方法对热图的处理效果要优于低通滤波及传统的两种P－M边缘函数的处理结果，为了更好地说明方法的优劣性，采用如下定义的信噪比(SNR)对方法的处理结果进行客观评价。

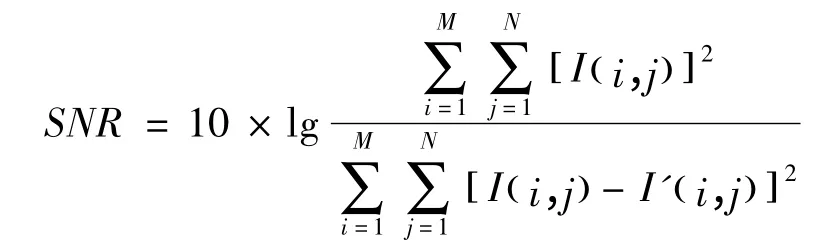
式中，I表示待处理的原始热图;I'表示去噪处理后的热图;M和N分别表示图像像素的长度和宽度。信噪比越大，表明算法处理的效果越好。上述四种方法处理后图像的信噪比如表1所示。

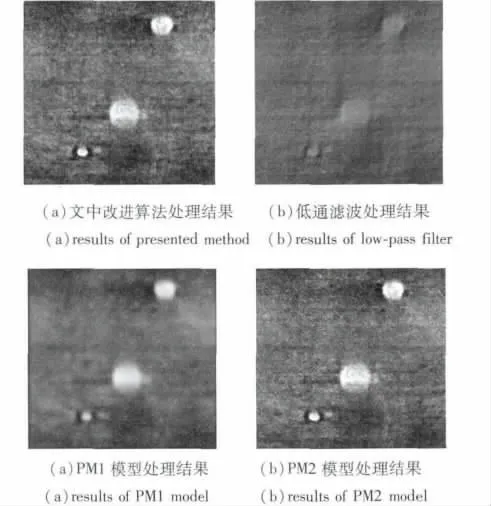
图7 原始热图去噪增强结果Fig.7 Denoising and enhancement of original thermal image

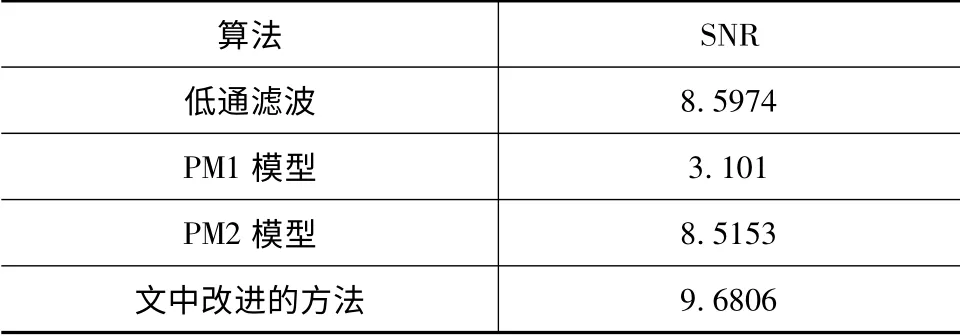
表1 图像处理结果的信噪比Tab.1 SNR of image processing

从表1中的结果可知，改进后偏微分算法的SNR要优于其他三种方法，这也证明了文中改进算法在热图去噪处理中的有效性。

6 结论

文中对红外热波检测图像的噪声进行了分析研究，为了解决热波检测图像高噪声、低对比度等问题，提出了一种改进的非线性偏微分方程方法。研究了偏微分方程在图像处理应用中的数学基础，针对热波图像本身的噪声特点，对现有的非线性偏微分方程模型进行了改进，并将处理结果与传统PM方程的结果进行对比，试验结果表明:文中提出的改进算法能够明显去除原始热图中的噪声，改善图像的质量。

参考文献:

［1］ Xiangzhi Bai，Fugen Zhou，Bindang Xue．Infrared image enhancement through contrast enhancement by using multiscale new top-hat transform［J］．Infrared Physics＆Technology，2011，54(2):61－69．

［2］ Francisco J．Madruga，Clemente Ibarra-Castanedo，Olga M Conde，et al．Infrared thermography processing based on higher-order statistics［J］．NDT＆E International，2010，43(8):661－666．

［3］ W L Gong，Y X Gong，A F Long．Multi-filter analysis of infrared images from the excavation experiment in horizontally stratified rocks［J］．Infrared Physics＆Technology，2013，56:57－68．

［4］ LIU Tao，ZHANG Wei，HE Fujun，et al．Research on image enhancement in infrared thermal waves NDT［J］．Infrared and Laser Engineering，2012，41(7):1922－1927．(in Chinese)刘涛，张炜，何付军，等．红外热波检测方法图像增强环节研究［J］．红外与激光工程，2012，41(7):1922－1927．

［5］ LIU Tao，XU Weichang，TANG Tao，et al．Application of wavelet transform to images enhancement in thermal wave NDT［J］．Laser＆Infrared，2012，42(6):709－712．(in Chinese)刘涛，徐卫昌，唐涛，等．小波变换在热波检测图像增强中的应用［J］．激光与红外，2012，42(6):709－712．

［6］ XU Weichang，HUANG Wei，LI Yongfeng，et al．Application of low-pass filtering and gray adjusting to image enhancement［J］．Laser＆Infrared，2012，42(4):458－462．(in Chinese)徐卫昌，黄威，李永峰，等．低通滤波与灰度值调整在图像增强中的应用［J］．激光与红外，2012，42(4):458－462．

［7］ WANG Dakai，HOU Yuqing，PENG Jinye．Partial differential equation in image processing［M］．Beijing:Science Press，2008．(in Chinese)王大凯，侯榆青，彭进业．图像处理的偏微分方程方法［M］．北京:科学出版社，2008．

［8］ ZHANG Tong，ZHU Hong，ZHANG Ran，et al．Based on the dual-tree complex wavelet with 6 directional Wiener filter combine partial differential equation in image denoising［J］．Journal of Image and Graphics，2009，14(5):848－852．(in Chinese)张瞳，朱虹，张然，等．复小波域维纳滤波与偏微分扩散相结合的图像去噪方法［J］．中国图象图形学报，2009，14(5):848－852．

［9］ WANYAN Dandan．Study of infrared image contrast enhancement algorithm［D］．Luoyang:Henan University of Science and Technology，2012．(in Chinese)完颜丹丹．红外图像对比度增强算法研究［D］．洛阳:河南科技大学，2012．

［10］Perona P，Malik J．Scale-space and edge detection using anisotropic diffusion［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12(7):629－639．

［11］WU Wei，WANG Hongzhi，SONG Yu．Image denoising algorithm based on partial differential equation［J］．Journal of Changchun University of Technology:Natural Science Edition，2011，32(6):554－557．(in Chinese)武伟，王宏志，宋宇．基于偏微分方程的图像去噪算法［J］．长春工业大学学报:自然科学版，2011，32(6):554－557．

［12］WANG Yu，ZHANG Huiyan．Fluorescence microscopic image denoising based on forth-order PDEs and contrast enhancement［J］．Journal of University of Electronic Science and Technology of China，2012，41(4):564－567．(in Chinese)王瑜，张慧妍．基于四阶PDEs和对比度增强的荧光显微图像去噪［J］．电子科技大学学报，2012，41(4):564－567．

［13］WANG Lisheng，XU Zongben．Review on PDE-based image processing techniques and their applications in biomedical images analysis［J］．Chinese Journal of Engineering Mathematics，2004，21(4):475－490．(in Chinese)王利生，徐宗本．偏微分方程在生物医学图像分析中的应用［J］．工程数学学报，2004，21(4):475－490．

［14］Guillermo Sapiro．Geometric partial differential equations and image analysis［M］．New York:Cambridge University Press，2001．