单幅干涉条纹图相位提取新算法

郭 媛，陈小天，毛 琦，赵丽娜

(齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔161006)

1 引言

电子散斑干涉测量技术具有非接触、全场测量、精度高和隔震要求低的特点［1－3］，已成为动态和静态物体变形测量的一种重要方法。散斑测量得到干涉条纹图，需要从变形的条纹图中提取相位信息，从而获得所测的物理量。应用于相位解调的方法主要有相移法［4－5］和傅里叶变换法［6－7］。相移法不仅过程复杂，而且得到的是包裹相位，需要进行解包裹运算。傅里叶变换法虽然简单，但得到的也是包裹相位，同样需要再进行相位解包裹［6－7］。

相移法中常用的相位解包裹有路径跟踪法、最优估计法和最小范数法［8－10］。其中用到最多的是最小范数法中的最小二乘相位解包裹方法。最小二乘相位解包裹方法的原理是得到一个泊松方程，通过求解泊松方程就可以得到相移法所求的相位［11－12］。本文融合最小二乘相位解包裹得到泊松方程求解相位的方法和从单幅干涉条纹图中恢复相位的方法，提出新的单幅干涉条纹图恢复相位的新方法。通过对单幅干涉条纹图进行两次希尔伯特变换提取干涉条纹图中的余弦分量和正弦分量，由正弦分量和余弦分量求取相位的正切值，即相位的梯度［13］。从相位梯度得到泊松方程，从而变成了求解泊松方程。这种方法不仅能够从单幅干涉条纹图中恢复真实相位，并且由希尔伯特变换可以滤除干涉条纹图中的直流分量的噪声，达到滤波的效果，而且减小了相移法的复杂性。实验验证了该方法的可行性和正确性。

2 单幅干涉条纹图提取相位基本理论

2．1 希尔伯特变换

希尔伯特变换Hilbert transform(HT)是在时域中进行的一种特殊正交变换。在一维实空间中，信号f(x)的希尔伯特变换是f(x)和1/πx的卷积。定义信号f(x)的希尔伯特变换为［14－15］:

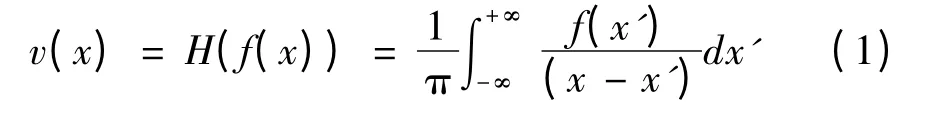
在频域中，希尔伯特变换的结果来自sign函数的简单乘积，即:

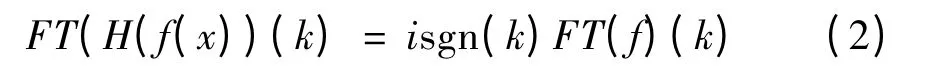
其中，FT为傅里叶变换;k为角频率，并且:

希尔伯特变换等同于一个滤波器，一个信号经过希尔伯特变化后，只是把它在频域相移π/2。在频域内，希尔特变换的关系可表示为

式中，V(f)是函数v(x)的傅里叶变换;U(f)是函数f(x)的傅里叶变换;j是虚数单位。由希尔伯特变换的性质可知信号cos的希尔伯特变换就是sin，并且能够滤除原信号的直流分量，即可以有效地滤除原信号所携带的噪声。

2．2 基于离散余弦单幅图相位提取

通常，从动态散斑术中获得的散斑干涉图可以用式(5)表示:

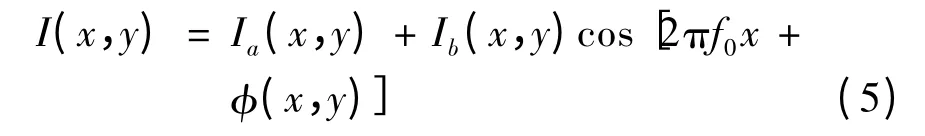
式中，Ia(x，y)为背景光强;Ib(x，y)为条纹幅值;f0为 载波的角频率;(x，y)为调制相位。Ia(x，y)和Ib(x，y)是缓变函数，可以视为常数。对于散斑条纹图进行希尔伯特变换得到正弦分量:

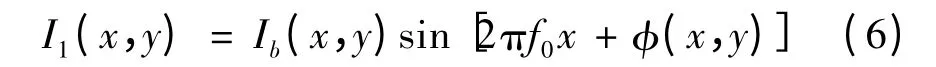
可看到希尔伯特变换很好地滤除了散斑干涉图中的直流分量，达到滤除噪声的效果。再次对I1(x，y)进行希尔伯特变换得到余弦分量:

令 (x，y)=2πf0x+(x，y)，则可以得到相位在x方向上的梯度［13，16］:

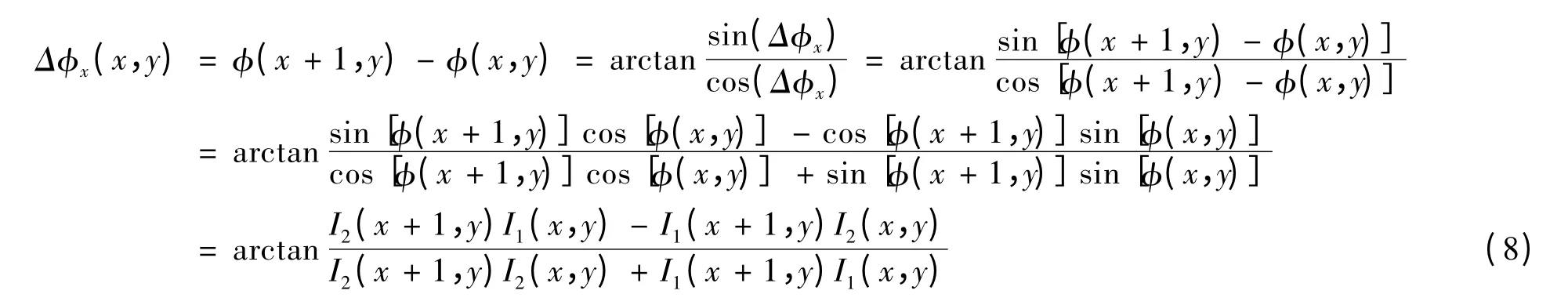
同理，相位在y方向上的梯度为:

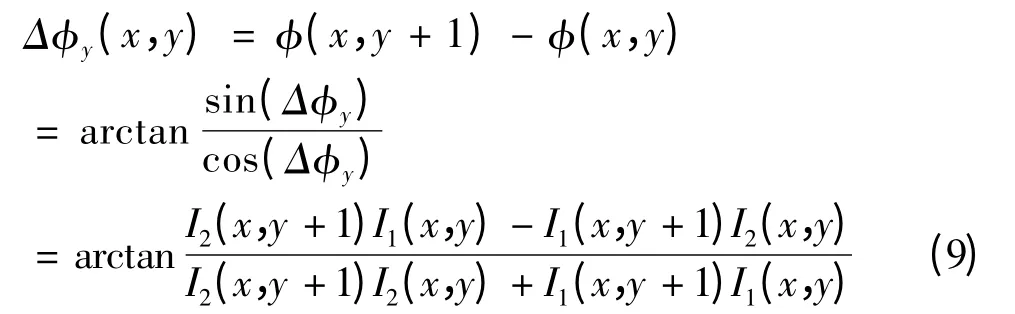
由式(8)和式(9)可以得到:

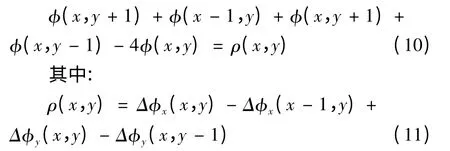
显然式(10)是M×N矩阵网格上的离散泊松方程，即:

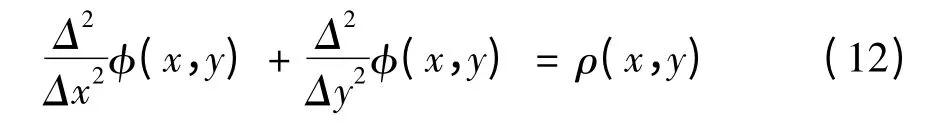
因此，计算相位在数学上等于求解离散泊松方程，用离散余弦变换(DCT)即可求出(x，y)，也就可得到本文中所求的真实相位。

在最小二乘相位解包裹［11］中常用DCT解泊松方程，但当残差点较多时DCT非加权最小二乘相位解包裹算法的计算结果比较平滑，从而有学者引入权重，抑制误差的传播，称为加权离散余弦变换(WDCT)［17］。为补偿其平滑作用，采用加权处理。权重定义为:

式(13)中，unit(·)为归一化处理;filt［·］为均值滤波。求出权重ui，j后，用ui，j对ρi，j进行加权处理:

其中，ρ*(x，y)是ρ(x，y)加权处理的结果，然后利用对泊松方程的求解即可求出真实相位。鉴于WDCT算法的优势，实验采用WDCT算法解泊松方程。

3 实验与结果分析

相移法提取散斑干涉条纹图首先需要经过相移(如四步相移法)提取包裹相位，再通过相位解包裹运算才能够解开包裹相位得到真实相位。而本文提出的基于离散余弦的的方法能够简便的完成相移法的过程，从散斑干涉条纹图中直接得到真实相位。相移法和本文提出的方法基本流程对比图如图1所示。

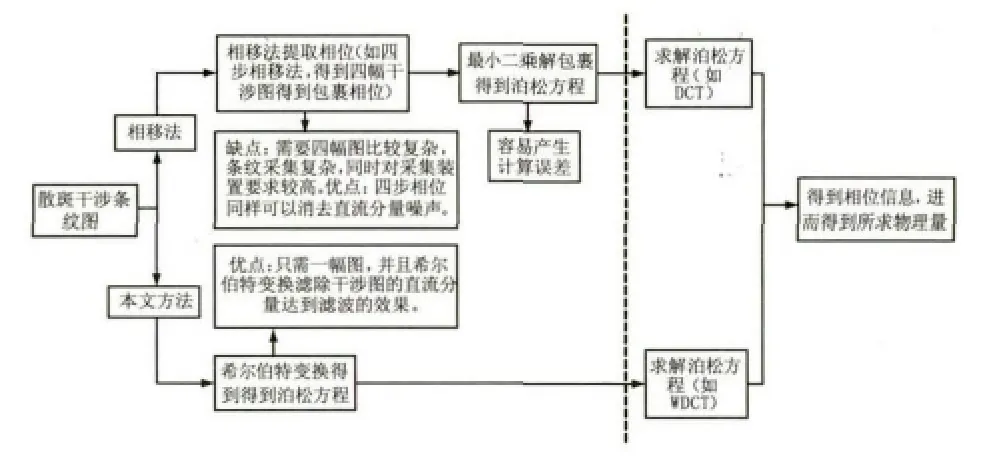
图1 相移法和本文提出的方法从干涉条纹图提取相位对比流程图Fig．1 The flow chart of phase-shift and the proposed method extracted phase from interference fringe patterns

用MATLAB生成400×400的散斑干涉条纹图，条纹图的强度分布为:

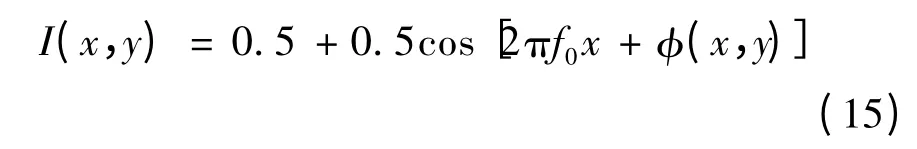
其中，f0为载波频率，大小取0．125，(x，y)=2peaks(400)。相移法是对干涉条纹图提取相位最常用的方法，用相移法提取干涉条纹相位如图2所示，首先模拟四幅光栅干涉条纹图，用四步相移法从中提取包裹相位，四步相移法提取包裹相位方法见参考文献［4］。再用最小二乘方法得到泊松方程［11－12］，最后用WDCT方法求解泊松方程得到真实相位。

图2 用4步相移法从4幅干涉条纹图中提取相位的结果Fig．2 Results of the phase extracted from 4 interference fringe patterns by phase-shift method

用本文提出的基于离散余弦的方法从干涉条纹提取相位结果如图3所示，从图3中可以看出本文提出的方法同样能够很好地干涉条纹图中提取真实相位。图3(d)中最小二乘求解相位(LSDCT)曲线是经过四步相移提取包裹相位，再经过最小二乘法解包裹提取的真实相位，与本文提出的基于离散余弦提取相位的曲线是重合的，图中小坐标是x等于150处的局部放大图。尽管相移法提取相位和本文提出的方法提取相位的误差是一样的，但是本文提出的算法只需要一幅干涉条纹图，就能够发到相移法所能够达到的结果。大大降低了从干涉条纹图提取相位的现实要求，降低了相位提取的繁琐程度，而且缩短了相位提取的时间，相移法提取真实相位时间为6．8 s，而本文提出的方法提取真实相位时间为2．8 s。同时，现实中相移法受环境因素会更大，故本文提出的算法更适合应用于实际干涉条纹相位提取。

对于现实含有噪声的干涉条纹图提取相位如图4所示，如图4(a)所示的含有噪声的干涉条纹图，用相移法提取的相位如图4(b)所示，用本文提出的方法提取的相位如图4(c)所示。

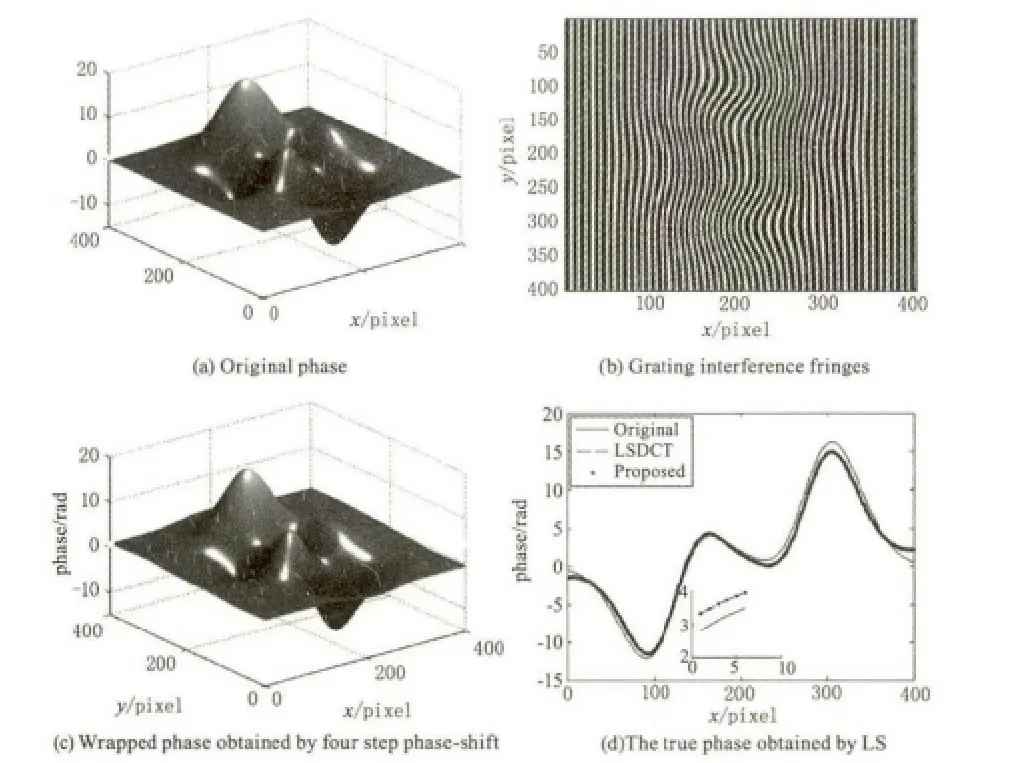
图3 用本文从单幅干涉条纹图中提取相位的结果Fig．3 Results of the phase extracted from a single interference fringe pattern by the proposed method

图4 用两种方法对含有噪声的相位提取Fig．4 Comparing of phase extracted with noise by two method

从图4中可以看出本文提出的基于离散余弦的方法同样能够很好地从单幅图中提取真实相位，并没有因为该方法过程简单而导致误差增多。相反，在现实情况中相移法，需要多幅条纹图，导致每幅图含有不一的噪声，从而导致更多的误差。

4 结论

通过上面一系列的实验可以看出本文提出的方法能够很好地从单幅干涉条纹图中提取真实相位，与之相比，相移法需要4幅干涉条纹图，过程复杂，对光学采集系统的要求较高，提取的4幅干涉条纹图进行计算得到包裹相位，还需相位解包裹才能得到真实相位。而本文提出的算法只需要1幅干涉条纹图就能够解出真实相位，环境因素的影响比相移法小。同时相位提取的误差在理想的情况下是相同的，但由于各种因素的影响，现实情况下本文提出的算法得到的结果会更好。

［1］ ZHOU Jie，XU Manping．Application of electronic speckle measurement of the refractive index of phase objects［J］．Laser＆Infrared，2010，40(2):192－194．(in Chinese)周杰，徐满平．应用电子散斑测量位相物体的折射率［J］．激光与红外，2010，40(2):192－194．

［2］ MI Honglin．Speckle pattern interferometry technique based on laser and Its application in measured displacement［J］．Laser Journal，2013，34(5):23－24．(in Chinese)米红林．基于激光的散斑干涉术及其测量中的应用［J］．激光杂志，2013，34(5):23－24．

［3］ LIU Hengbiao，WANG Changling．Roughness measurement of shot-blasted surface based on polychromatic speckle autocorrelation［J］．Acta Optica Sinica，2010，30(9):2578－2584．(in Chinese)刘恒彪，王昌灵．抛喷丸表面的多波长散斑自相关法粗糙度测量［J］．光学学报，2010，30(9):2578－2584．

［4］ WU Lushen，WAN Luping，LI Yuwen．Phase-stepping error analysis of 3D measuring system based on phase method［J］．Laser＆Infrared，2012，42(9):1040－1044．(in Chinese)吴禄慎，万露萍，李彧雯．基于相位法的三维测量系统的相移误差分析［J］．激光与红外，2012，42(9):1040－1044．

［5］ DENG Lijun，YANG Yong，SHI Bingchuan，et al．Twostep phase-shifting digital holography based on extraction of phase shift［J］．Chinese J．Lasers，2014，41(2):0209014．(in Chinese)邓丽军，杨勇，石炳川，等．基于相移量提取的两步相移数字全息术［J］．中国激光，2014，41(2):0209014．

［6］HUANG Fang，ZHANG Wenjing，WANG Haiyan，et al．Object deformation measurement based on FFT speckle pattern interferometry［J］．Laser＆ Infrared，2012，42(2):124－128．(in Chinese)黄芳，张文静，王海燕，等．基于FFT的散斑干涉术测物体变形［J］．激光与红外，2012，42(2):124－128．

［7］ MENG Fanwen，WU Lushen．Study on 2-D fourier transform based on FTP［J］．Laser＆Infrared，2008，38(9):955－957．(in Chinese)孟凡文，吴禄慎．基于FTP的二维傅里叶变换的研究［J］．激光与红外，2008，38(9):955－957．

［8］ Y T Zhang，Min-JH，Hua-R L，et al．Branch cutting algorithm for unwrapping photoelastic phase map with isotropic point［J］．Opt Laser Eng，2012，50:619－631．

［9］ Q Liu，Y Wang，F Ji，et al．A three-step least-squares iterative method for tilt phase-shift interferometry［J］．Opt．Express，2013，21(24):29505－29515．

［10］M Yan，L Wang．Weighted Kalman filter phase unwrapping algorithm based on inSAR image［J］．Engineering Review，2013，33:227－231．

［11］QIAN Xiaofan，LI Bin，LI Xinghua，et al．Improvement of least-square phase unwrapping algorithm based on lateral shearing interferometry J］．Chinese J．Lasers，2012，39(11):1109002．(in Chinese)钱晓凡，李斌，李兴华，等．横向剪切最小二乘相位解包 裹 算 法 的 改 进［J］．中 国 激 光，2012，39(11):1109002．

［12］GUO Yuan，CHEN Xiaotian．Study of improved phase unwrapping algorithm based on least squares［J］．Chinese J．Lasers，2014，41(5):0508005．(in Chinese)郭媛，陈小天．基于最小二乘相位解包裹改进算法的研究［J］．中国激光，2014，41(5):0508005．

［13］XIONG Liudong，JIA Shuhai，DU Yanfen．A novel algorithm for phase retrieval from a single carrier-frequency fringe pattern［J］．Acta Optica Sinica，2010，30(1):123－126．(in Chinese)熊六东，贾书海，杜艳芬．单幅载频条纹图的相位恢复新算法［J］．光学学报，2010，30(1):123－126．

［14］Shouyu Wang，Liang Xue，Jiancheng Lai，et al．An improved phase retrieval method based on Hilbert transform in interferometric microscopy［J］．Optik，2013，124(14):1897－1901．

［15］Mustapha B，Mohamed A，Elmostafa B．Optical phase extraction algorithm based on the continuous wavelet and the Hilbert transforms［J］．Journal of Computing，2010，2(5):1－5．

［16］Kemao Qian，Anand K Asundi．Algorithm for directly retrieving the phase difference:a generalization［J］．Opt．Eng，2003，42(6):1721－1724．

［17］DONG Chunmin，LIU Guolin，YU Shengwen，et al．An improved algorithm of weighted least-squares for phase unwrapping［J］．Journal of Geodesy and Geodynamics，2011，31(supp．):90－97．(in Chinese)董春敏，刘国林，于胜文，等．加权最小二乘相位解缠的一种改进［J］．大地测量与地球动力学，2011，31(增刊):90－97．