基于有限元的脉冲激光辐照材料温度场研究
2015-03-29周凤艳孙继华宋江峰陈建伟
马 健,赵 扬,周凤艳,孙继华,刘 帅,郭 锐,宋江峰,陈建伟
(1.山东省科学院激光研究所,山东 济南250014;2.山东省汽车工业集团有限公司,山东 济南250011)
1 引言
作为激光超声的激励源,脉冲激光能够以较大的峰值功率辐照于材料表面,一般认为激光超声波的产生基于热弹和烧蚀两种机理,热弹与烧蚀的主要区别为瞬间加载于物体表面上的激光能量是否引起表面熔化、气化。当激光的功率密度达到106~108W/cm2时,材料表面会发生气化。上述数值仅是一个范围,对于给定的激光功率密度,材料的温升还与吸收率、材料参数密切相关,能否引起材料的烧蚀却不好判断,这就需要建立一套有效的数值计算方法,用于求解脉冲激光辐照材料的温度场。
采用有限元分析材料受激光辐照的温度场是常用的热分析方法,鉴于目前有限元热分析文献中只是定性说明在激光辐照区域中网格划分要密集一些,或者直接定量指明网格的大小,以便得到精确的结果;而在其他区域单元网格尺寸取大一些,以减少计算量节省计算机资源[1-2],但是对于具体的选择依据没有做详细明确的表述。本文讨论了激光辐照材料表层的热分析时,单元网格的大小对有限元分析结果的影响,给出了以热扩散深度为依据的网格大小选取规则。最后,基于有限元热分析的温度数据,给出了应力场的计算结果。
2 理论基础与数值计算
2.1 理论模型
图1所示为材料受激光辐照的模型,x,y,z分别表示直角坐标系中的三个不同方向上的坐标,单位m。受激光辐照的物体为圆柱体,其对称轴为y轴,辐照中心与坐标系原点重合。激光器发射出重复频率5 Hz直径为6 mm的脉冲激光,脉冲宽度为10 ns,波长为1064 nm。辐照区域内脉冲激光功率密度的表达式为:
式中,r,τ分别为点距光斑中心的距离与时间,单位相应为m,s,此时为光斑中心的功率密度;A为材料表面的吸收率;f(r)和g(τ)分别为激光功率密度的空间分布和时间分布。事实上,激光辐照材料表层的过程极其复杂,用有限元法完全模拟出激光辐照的实际情况是不可能的,为了尽可能的反应实际情况并有效地简化问题,现提出以下假设:①环境温度为300 K。②材料的导热性能是均匀的而且各向同性。③忽略固相之间的转换对温升规律的影响。④将材料与工作台接触面上的散热量忽略,其余各面均存在对流换热与辐射换热,引入总换热系数h进行分析[3]。

图1 材料受激光辐照的理论模型Fig.1 Model for material surface irradiated by laser
2.2 导热微分方程及边界条件
获得材料受激光辐照的温度场分布,需要根据能量守恒定律和傅里叶定律来建立温度场的导热微分方程,无内热源的三维非稳态导热微分方程[4]如下:
式中,T为温度,K;λ为导热系数,W/(m·K);ρ为材料的密度,kg/m3;c为材料的比热,J/(kg·K)。考虑材料的热物性时,λ、ρ、c均为变量,否则λ、ρ、c均为常量。其余参数含义同上。
对于式(2),为获得方程的唯一解,需要附加一定的边界条件和初始条件,根据前提条件及假设,在脉冲激光辐照时(τ0≤τ≤τ0+τp),材料y=0表面上激光辐照区域中的单元存在着热流载荷[5]:
除了材料与工作台相接触的面,其余各表面存在着对流与辐射换热,换热边界条件为:
式(3)、(4)中,τ0为每个脉冲激光的起始时刻;τp为脉冲宽度,本文中τp=10 ns;n表示表面的法向矢量;Γ是材料的边界;T0是环境温度。
初始条件:T0=300 K。
2.3 激光辐照材料温度场的有限元分析
脉冲激光的时间分布g(τ)取为矩形,空间分布f(r)为高斯平顶分布,经由点聚焦镜透射并通过遮挡去除边缘部分之后,在材料表面形成直径D=1.8 mm、能量分布均匀的圆形光斑,圆形光斑具有的单脉冲能量为10.2 mJ,经过计算I(r,τ)=1×107W/cm2。首先以航空航天中常用的热障涂层系统为研究对象,对单次脉冲辐照时的情况进行有限元分析和数学解析。其中表面陶瓷层的厚度为200μm,直径为1.8 mm。为了便于有限元求解结果与理论解析值的对比,暂不考虑材料的热物性,忽略热障涂层各成分界面上的热交换,并将A、h视为恒定值,大小分别为0.25、0。表1中为表面陶瓷层的材料参数[6]。通过对比有限元求解结果和温度场理论值,验证辐照材料表层温度场有限元求解方法的正确性,并得出辐照区域网格尺寸的划分依据。

表1 陶瓷层的参数Tab.1 Parameters of Ceramic Top Coat
在脉冲激光作用完毕的时刻,热扩散深度为[7]:

式(5)中,D为热扩散率,m2/s,其计算方法为:

根据式(5)求出热扩散深度为1.6×10-7m。
首先利用有限元分析软件对陶瓷层进行瞬态热分析:①建立2.1节所述的理论模型并分配材料参数,根据模型的轴对称性选择四节点轴对称单元,将三维热分析问题转换为轴对称问题进行处理。为获得不同网格划分下的温度场计算结果,分别按照脉冲激光结束时热扩散深度的1倍、1/2倍、1/4倍、1/8倍、1/10倍离散模型。②选择分析类型为瞬态热分析,设置环境温度为300 K,总的分析时间长度为1μs。为了便于处理,时间轴零点取为单个脉冲的起始时刻。0~10 ns对材料受辐照区域施加热流密度载荷,为了获得精确数据,时间步长取为1 ns;随后卸载载荷,在11 ns~0.2μs区域中,时间步长取为2 ns。而在其余时间内,为了提高计算效率,时间步长取为20 ns。③直接求解获得温度场,求解完毕后进行时间历程分析,提取节点温度随时间的变化规律。该有限元分析所用计算机的主要配置为8核I7-3770 CPU处理器,16GB内存。将各网格划分下获得的节点温度最大值列于表2中。图2为h/4网格划分下,有限元求解出的脉冲激光辐照陶瓷层的温升曲线。
其次对陶瓷层的温度场进行理论解析,以验证有限元热分析结果的正确性。当垂直入射的激光束覆盖了整个y=0表面,以及热扩散深度远小于光斑大小以及陶瓷层的厚度时,辐照表面中心下方区域的温度计算可以简化为一维处理,则激光加热和冷却过程中的瞬态温度场解析公式为:

式中各参数的含义均同上。
根据式(7)和已知参数,利用MATLAB编写程序,计算辐照表面中心及其正下方位置的温度场,得到表层图3中的曲线和温度最大值为1557 K。对比图2和图3,温度场的有限元分析结果和理论解析结果均呈现以下规律:表面中心点的温度在脉冲结束时刻达到最大值,然后温度缓慢下降;而表面下方各处的温度升至最高点的时刻逐渐滞后,温度最大值也随深度的增加而减小。通过对比可知,温度场有限元结果与理论解析结果有较好的吻合。

表2 有限元计算结果Tab.2 Data of finite element calculation
表2同时表明随着网格尺寸的减小,辐照中心节点的温度最大值不断增大,有限元分析结果逐渐逼近理论值。但所需的计算时间和产生的数据量显著增加,而相对误差减小的幅度却逐渐降低。当网格尺寸取热扩散深度的1/10时,有限元结果和理论值之间的相对误差为1.24%,单纯追求有限元求解结果与理论值的逼近性,而大量增加计算机资源的消耗并不可取。一般情况下,可以取网格尺寸为脉冲激光结束时热扩散深度的1/4,此时,有限元结果和理论值之间的相对误差为2.38%。

图2 辐照中心及下方节点的温升曲线的有限元计算结果Fig.2 Temperature curve of irradiated center and below nodes for finite element results

图3 辐照中心及下方节点的理论温升曲线Fig.3 Temperature curve of irradiated center and below nodes for theory results
3 有限元网格划分依据及应力场分析
由上可知,有限元求解脉冲激光辐照材料的温度场时,应以脉冲激光结束时的热扩散深度作为依据,综合考虑计算精度和所需消耗的计算机资源,选取受辐照区域的网格大小。对于热物性比较明显的材料,在脉冲激光结束时刻辐照区域的温度场未知,与温度相关的材料参数值无法具体选取,相应的热扩散深度亦无法具体求出。此种情况下,则根据各温度点求出脉冲激光结束时热扩散深度的最小值作为网格尺寸选取的依据。
相对于理论解析,利用有限元可方便求解复杂的问题,能够同时考虑材料热物性、对流与辐射换热、材料的相变潜热等多种因素。现给出一个具体分析实例:脉冲激光的参数同上,选取几何尺寸为直径20 mm,厚度10 mm铝质工件进行研究,铝的热物性参数[8]如表3所示。
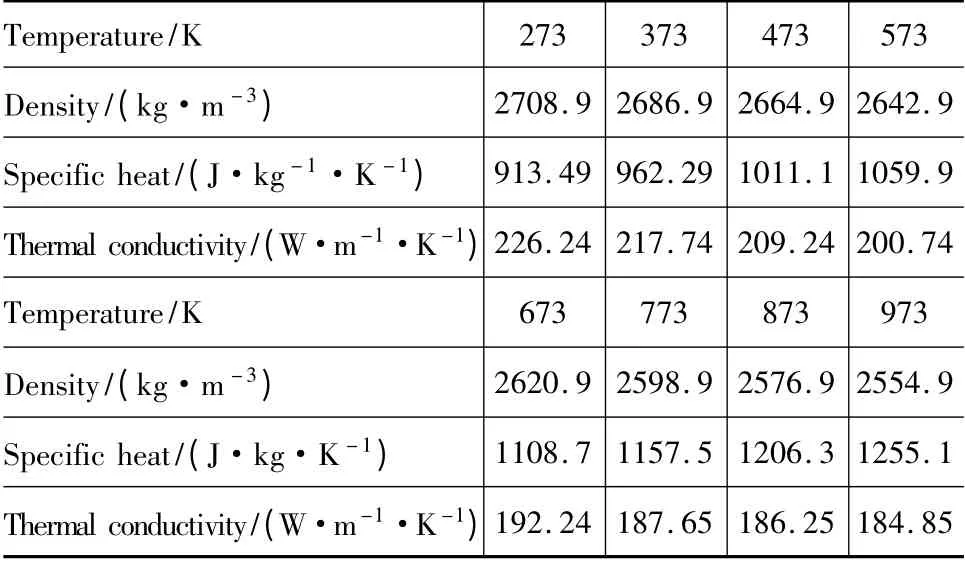
表3 铝的热物性参数Tab.3 Thermal parameters of aluminum(Melting point:933.4 K;boiling point:2740 K)
根据表3和式(5)求出热扩散深度的最小值为1.52×10-6m,取有限元模型网格尺寸为h/4(3.8×10-7m),依据建立的温度场有限元求解方法,计算铝质试块受脉冲激光辐照的温度场。图4为10 ns时刻铝质试块的轴截面右侧局部温度场,图5为辐照区域中心节点及其下方节点的温升曲线。

图4 10 ns时刻铝质试块的右侧局部温度场Fig.4 Partial temperature field of the right side of aluminum test block at 10 ns

图5 铝质试块的辐照中心节点及下方节点的温升曲线Fig.5 Temperature curve of aluminum test block for finite element results
由求解的温度场数据可以看出,辐照区域的最高温度为415.8 K,低于铝的熔点933.4 K。10μs时刻辐照中心点的温度已降至300.1 K,而5 Hz重复频率对应的脉冲间隔为200 ms。相比之下,铝质工件辐照区域降温所消耗的时间非常短,因此铝质工件辐照区域的温度数值可视为无累积效应。所以激光超声检测铝质工件时,加载脉冲宽度为10 ns,单脉冲能量为10.2 mJ,重复频率5 Hz的激光是允许的。
工件的局部的温度场发生变化,必然引起应力场的变化,进而导致超声波的产生。根据热障涂层和铝质工件温升的数值计算结果,二者辐照区域的最高温度均低于相应的熔点,所以激光超声波的产生符合热弹机理。忽略位移场对温度场的影响,采用耦合场分析中的间接法,将节点温度分析结果作为体载荷施加到结构应力分析中,可获得节点竖直方向上位移的时间历程曲线,图6和图7分别为200μm厚、直径20 mm热障涂层和10 mm厚、直径20 mm铝质试块的上表面节点位移随时间的变化,与学者沈中华[9]和王纪俊[10]得到的结果一致。

图6 热障涂层上表面节点竖直方向上的位移随时间的变化Fig.6 Displacement of the node for thermal barrier coating system

图7 铝质试块上表面节点竖直方向上的位移随时间的变化Fig.7 Displacement of the node for aluminum test block
4 结论
建立了材料受脉冲激光辐照的理论模型,针对辐照区域的温度场提出了有效的有限元求解方法,讨论了有限元计算中单元网格尺寸对计算结果的影响。在利用有限元求解脉冲激光辐照区域的温度场时,应以脉冲激光结束时的热扩散深度为依据,综合考虑计算精度和所需消耗的计算机资源等因素,确定网格尺寸。一般情况下,将受辐照区域中的网格大小取为脉冲激光结束时热扩散深度的1/4,这样既能够获得可靠的数据,又能降低对计算机资源的消耗。材料温升的有限元数值计算结果能够为激光能量的加载提供参考,并能够为后续应力场的瞬态分析提供体载荷。
[1] YUAN Liguo,ZHAO Guomin,JIAO Luguang.Preliminary study on the temperature history of metal/liquid structure under pulsed laser irradiation[J].Laser&Infrared,2010(1):18-21.(in Chinese)袁立国,赵国民,焦路光.脉冲激光辐照下金属/液体结构温度变化初探[J].激光与红外,2010(1):18-21.
[2] AN Fuping,CHEN Zhijun,YAO Jianhua,et al.Numerical simulation of temperature field on precipitation hardening SSafter laser solid solution and alloying synchronous hybrid strengthening[J].Applied Laser,2013,33(002):119-124.(in Chinese)安福平,陈智君,姚建华,等.沉淀硬化不锈钢激光固溶合金化同步复合强化温度场的数值模拟[J].应用激光,2013,33(002):119-124.
[3] LIU Zhuang,WU Zhaoji,WU Jingzhi,et al.Numerical simulation of the heat treatment process[M].Beijing:Science Press,1996:7-9(in Chinese).刘庄,吴肇基,吴景之,等.热处理过程的数值模拟[M].北京:科学出版社,1996:7-9.
[4] YANG Shiming,TAO Wenquan.Heat transfer[M].4th ed.Beijing:High Education Press,2006:42.(in Chinese)杨世铭,陶文铨.传热学[M].第4版.北京:高等教育出版社,2006:42.
[5] WU Sijie,ZHAO Xiaobei,YANG Dongsheng,et al.Laser damage in IR detector[J].Infrared and Laser Engineering,2013,42(5):1184-1188.(in Chinese)吴思捷,赵晓蓓,杨东升,等.激光辐照对红外探测器的损 伤[J].红 外 与 激 光 工 程,2013,42(5):1184-1188.
[6] BAI Yu-mei,XU Ying-qiang,LAI Ming-rong,et al.Analysis of Residual Stresses in Thermal Barrier Coating due to Thermal Mismatch[J].Science Technology and Engineering,2011,11(14):3126-3129.(in Chinese)白玉梅,徐颖强,赖明荣,等.热障涂层热不匹配残余应力的分析研究[J].科学技术与工程,2011,11(14):3126-3129.
[7] SUN Cheng-wei.Laser Irradiation Effect[M].Beijing:National Defense Industry Press,2002.1:4-66.(in Chinese)孙承纬.激光辐照效应[M].北京:国防工业出版社,2002.1:4-66.
[8] HE Yuejuan,CHEN Guoqing,SHEN Zhonghua,et al.The influence of the line-source laser's width on laser-induced temperature field in aluminum pipe[J].Laser Journal,2008,29(1):68-69.(in Chinese)何跃娟,陈国庆,沈中华,等.激光线源宽对铝管中温度场的影响[J].激光杂志,2008,29(1):68-69.
[9] SHEN Zhonghua,XU Baiqiang,NI Xiaowu,et al.Numerical simulation of laser-generated ultrasonic waves in layered plates[J].Journal of Physics D:Applied Physics,2004,37(17):2364-2370.
[10]WANG Jijun,SHEN Zhonghua,NI Xiaowu,et al.Numerical simulation of laser-generated surface acoustic waves in the transparent coating on a substrate by the finite element method[J].Optics&Laser Technology,2007,39(1):21-28.
