面向直升机低空突防的三维航线规划算法研究

李 钦，李 锋，杨振发，龙际梦

（信息工程大学 地理空间信息学院，河南 郑州450000）

直升机的低空突防航线规划［1］是指在特定工作空间中，从起始点到终止点，根据地形、环境威胁、直升机低空突防的任务要求及自身性能等约束条件，寻找一条符合这些约束条件的最优或次优飞行路径。一条好的航线既能规避周围的地形障碍，防止撞山事故的发生，同时也可以减少被雷达发现和高炮击中的概率，对直升机任务的顺利执行很有利，尤其在防空技术日益完善的现代战争中，航线规划是提高直升机作战效率，保证作战任务顺利完成的有效手段［2］。

近年来，在飞行器航线规划方面很多学者做了许多研究，这些研究主要围绕规划效率和航线质量展开。夏丛亮等研究了遗传算法［3－5］在低空突防领域中的应用［6］，得到的最优航线有效回避了威胁和地形，然而该研究却仅局限二维平面。刘丽峰等利用电势理论进行三维航线规划［7］，得到了可以避开各种威胁场的三维航线，然而这种方法却只针对于无人机，对于性能不同的直升机却难以适用。邱福生等采用遗传模拟退火算法进行航线规划，该方法仅在山峰和防空威胁区数量较少时规划效率高［8］，面对直升机低空突防中的复杂战场环境将难以适用。

总体来讲，这些方法对直升机低空突防三维航线规划缺乏针对性。基于此，本文综合考虑影响直升机突防航线的各种因素，提出了一种专门面向直升机突防三维航线规划的算法。

1 低空环境建模

在直升机进行低空飞行过程中，不仅面临极其复杂的战场地理环境，同时也受到战场电磁环境［9］的干扰威胁。一方面直升机近地飞行，面临着复杂地形环境的威胁；另一方面，直升机在飞行过程中也受到雷达电磁干扰、防空火炮击毁等威胁环境的影响 直升机低空航线规划的首要原则是需要避开地形、雷达、高炮等各种威胁，因此建立低空环境的表示模型是十分必要的，目前栅格法是空间离散建模的有效方法，即按照一定的采样间隔进行空间划分。根据飞行环境中的地形碰撞、电磁干扰、火炮打击等毁伤威胁因素计算格网单元的通行属性。

1．1 空间环境层次剖分

将规划空间进行栅格划分［10－11］是直升机低空突防航线规划算法研究的基础。这里假设规划区域是规则的长方体区域以方便建立空间参考基准。设规划区域长宽高分别为X，Y，Z，定义航线规划的局部坐标系：坐标原点定义在规划区域左下角点，坐标轴方向分别沿着长宽高增长的方向。综合考虑算法的精确度和效率，设定合适的采样间隔a，将规划空间划分成一系列边长为a的立方体栅格。

根据栅格单元对直升机飞行的影响，空间栅格的通行属性分为障碍栅格与自由栅格。障碍栅格指直升机无法通行或通行极度危险的空间栅格，是由地形障碍、雷达探测、火力威胁等因素造成的；自由栅格指直升机可自由通行，不存在任何安全隐患的栅格单元，是直升机航线规划可选栅格。

为确保直升机安全飞行，避免撞山事故的发生，通常要求直升机飞行高度超出地面一定距离，将地形表面之上一定高度范围内的区域内的栅格设置为障碍栅格，确保在规划航线时不会发生撞地事故（如图1所示，红色立方栅格即为障碍栅格，高低起伏的灰度面表示该地区地形面）。

图1 地形影响下的障碍栅格

1．2 威胁环境建模

直升机在飞行过程中，可能面临诸多威胁，如雷达探测威胁、高炮打击威胁。根据威胁源的类型和工作原理，计算威胁源影响区域，以此确定栅格单元的通行属性。

1．2．1 雷达威胁建模

雷达是长距离探测、识别和跟踪目标最重要的设备，雷达方程（描述雷达系统特性的最基本的数学方程）为

在建立模型时，由于目标到雷达之间的距离R对雷达的发现概率起着重要作用，而雷达又存在一个最大作用距离Rmax，所以可以简化雷达探测概率模型，用式（2）近似表示为

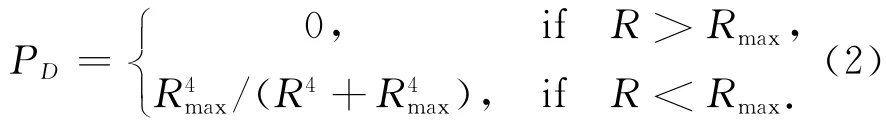
为了躲避雷达对直升机的探测，规划航线时要保证直升机与雷达之间的距离大于雷达的最大作用范围Rmax，为了模拟雷达对航线规划的影响，将以雷达中心为原点，Rmax为半径的球形区域覆盖空间内的栅格设置为障碍栅格，保证规划出的航线不会被雷达探测到。

1．2．2 防空火炮威胁建模

直升机进入防空火力范围，面临被击毁的危险，距离越近，被击毁的概率越大，在防空火炮火力打击范围内，直升机被击落的概率为

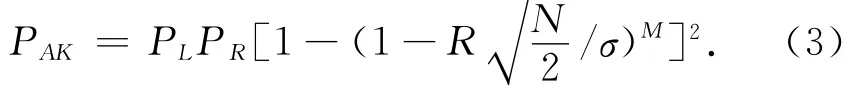
其中：PAK为杀伤概率；PL为发射可靠概率；PR为火炮雷达正常工作概率；R为炮弹杀伤半径；σ为射击偏差；M为射击次数；N为弹药数目。

为了保障直升机的安全飞行，规划航线时要确保直升机时刻位于火炮杀伤范围之外，即直升机与火炮的距离要时刻大于炮弹杀伤半径R。将以火炮位置为原点，R为半径的球形区域所在的空间内的栅格设置为障碍栅格，模拟直升机无法通过此区域，确保直升机不被击毁。

2 航线规划算法

直升机规划出的航线应使其避开障碍栅格，同时航线应尽可能的短，基于这一原则，构建初始栅格路径时采用领域搜索策略，一方面领域搜索是在领域中的自由栅格中搜索，另一方面距离目的地较近的自由栅格以较高的概率被选择；采用回退策略，即若领域中全是障碍栅格，则从栅格路径中删除当前栅格，并将当前栅格设置为障碍栅格，回退到栅格路径中上一栅格重新搜索，以此保证初始栅格路径一定可以生成，不会陷入“死胡同”；在初始栅格路径的基础上，为了简化存储和判断，删除栅格路径中无关紧要的自由栅格，得到简化后栅格路径，进而根据障碍物分布提取简化后栅格路径中的关键转折点，各转折点对于规避障碍物以及满足直升机自身性能限制都至关重要，最后首尾相连各转折点便规划出了航线 该航线首先一定是安全的即不会发生撞山、不会被探测到也不会被击毁，同时，各航线段都满足直升机性能的限制，最后邻域搜索策略保证了该航线长度相对较短。

2．1 初始栅格路径生成

初始栅格路径是指一系列首尾相连由起始栅格通向目标栅格的栅格集合，用记录表L1：（S（P0），P1，P2，…，Pn，D（Pn＋1））表示，其中S为起始栅格，D为目标栅格。若Pi为L1当前记录的栅格。

定义集合U（i），Pj∈U（i），则Pj为栅格单元Pi的上下左右前后栅格中的自由栅格且Pj尚不属于L1。则L1选择记录下一个栅格单元Pj的概率定义为

其中：Dj→D表示栅格单元Pj与目标栅格的距离，Dmax为U（i）中栅格距离目标栅格的最大值，式（4）表明距离目标栅格越近，被选择的概率越大。初始栅格路径生成步骤如下：

1）记录表L1记录起始栅格S，定义i＝0；

2）L1当前记录栅格为Pi，判断U（i）是否为空集；

3）如果U（i）为空集，若i＝0，直接退出，无法规划航线；否则将当前记录点Pi设置为障碍栅格，并从L1中删除当前记录点Pi，令i＝i－1，返回2）；

4）如果U（i）不为空集，判断目标栅格D是否属于U（i）；

5）若D属于U（i），L1记录D，算法结束；

6）若D不属于U（i），则依照式（4）按一定的概率在U（i）中选择下一个路径栅格，令i＝i＋1，返回2）。

通过这些操作便一定能生成可通行的栅格路径（如图2所示，图中红色方格即为威胁源作用范围内的障碍栅格，黄色栅格即为生成的栅格路径，S，D分别为起始点与终止点，灰度面代表地形面）。

2．2 提取关键转折点

2．2．1 初始栅格路径简化

在得到记录表L1后，为了简化初始栅格路径，删除那些对于决定航线无关紧要的栅格，仅保留一些关键栅格，这里定义关键栅格为：对于记录表L1记录下的路径栅格（S（P0），P1，P2，…，Pn，D（Pn＋1）），若Pi－1·x＝Pi·x＝Pi＋1·x且Pi－1·y＝Pi·y＝Pi＋1·y或者Pi－1·x＝Pi·x＝Pi＋1·x且Pi－1·z＝Pi·z＝Pi＋1·z或者Pi－1·y＝Pi·y＝Pi＋1·y且Pi－1·z＝Pi·z＝Pi＋1·z（1＜i＜n＋1）则Pi不是关键栅格，否则Pi为关键栅格。简化Li步骤如下：

图2 初始栅格路径

1）建立记录表L2用于记录简化后的L1，首先记录初始点S，定义变量i＝1；

2）判断Pi点是否为终止点D，若是，将Pi录入L2，算法结束；若不是，则继续执行；

3）判断Pi是否为关键栅格；

4）若Pi不是关键栅格，令i＝i＋1，继续执行2）；若Pi为关键栅格，将Pi录入L2，令i＝i＋1，继续执行2）。

通过以上算法便可得到记录表L2：（S（Q0），Q1，Q2，…，D）记录的简化栅格路径（如图3所示，图中红色方格即为威胁源作用范围内的障碍栅格，黄色栅格为简化后的栅格路径，S，D分别为起始点与终止点，灰度面代表地形面）。

图3 简化后栅格路径

2．2．2 关键转折点提取

对于简化后栅格路径表L2依然存在很多没有必要的节点，需要从L2中提取关键转折点形成最终的航线。各关键转折点必须同时满足以下3个条件：

1）各关键转折点前后相连形成的航线不穿过障碍栅格。

2各转折点处的转折角α前一航线段的延长线与下一航线段的夹角，如图4所示）必须小于直升机最大转弯角δ1。

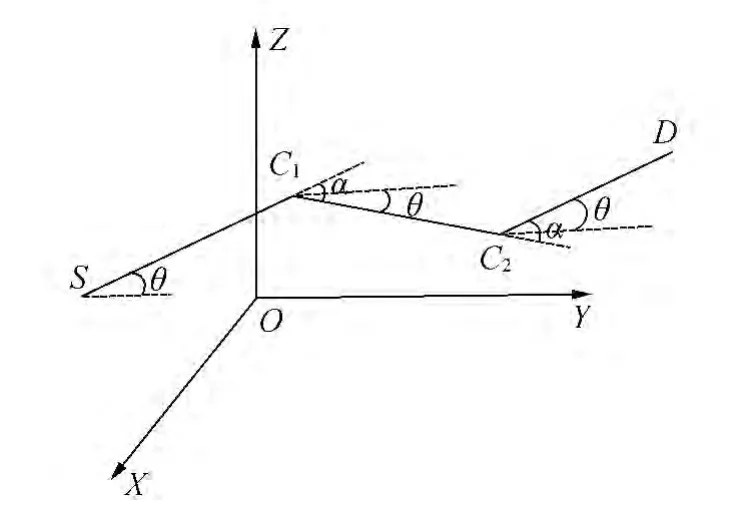
图4 转折角、垂直倾斜角示意图

3）相邻转折角之间的每条航线段的向上或向下垂直倾斜角θ（各航线段与水平面的夹角，如图4所示）必须小于直升机最大俯仰角和俯冲角δ2。

设关键转折点记录表L3：（S（C0），C1，C2，…，D），其生成步骤如下：

①用L3将S记录为转折点，定义i＝0；

②设L3当前记录点为Ci，L2中Ci之后的第一个点为Qj，若Qj＝D，将终止点D录入L3，程序结束，否则算法继续；

③若Qj＝D，将终止点D记录为转折点，程序结束；否则判断Qj与Ci连线是否穿过障碍栅格；

④若不穿过，令j＝j＋1，返回③；否则，进入⑤；

⑤判断Qj－1与Ci的连线是否满足关键转折点条件②、③；

⑥若满足，L3记录Qj－1，i＝i＋1返回②；

⑦若不满足，令j＝j－1，返回⑤。

通过以上算法在简化路径表L2的基础上便可以得到包括起始点和终止点的一系列航线关键转折点，首尾相连各关键转折点的控制点（即为栅格单元中心）便可以得到理想航线（如图5所示，图中红色方格即为威胁源作用范围内的障碍栅格，黄色栅格即为最终提取的关键转折点，各关键转折点前后相连的黑色折线段即为规划出的航线，S，D分别为起始点与终止点，灰度面代表地形面），该航线不仅避开了各威胁区域，而且各航线段都满足直升机最大转弯角和最大俯仰和俯冲角的限制。

3 算法实现与仿真实验

图5 航线生成

为了检验算法的可行性，采用青岛地区地形数据，地形幅面为2 242 m×3 088 m，对地形、雷达、防空火炮威胁区域以及使用本文算法所规划出的航线进行绘制，仿真结果如图6～图9所示，（图中S，D分别为起始点与终止点，绿色方格为防空火炮威胁作用范围内的障碍栅格，红色栅格为雷达探测作用范围内的障碍栅格，黄色栅格为提取的关键转折点，黑色折线段即为规划出的航线，高低起伏的灰度面为地形面）。图6为仅考虑地形威胁时规划出的航线，航线有效的避开了山峰，且航线相对较短；图7、图8分别为在综合考虑地形和防空火炮威胁以及地形和雷达探测威胁的条件下规划出的航线；图9为综合考虑各种威胁因素，包括地形、雷达探测、防控火炮威胁的条件下规划出的航线，该航线一方面避开了所有的威胁区域（地形、雷达、火力打击等覆盖区域），另一方面航线中的各航线段均满足直升机最大转弯角和最大俯仰和俯冲角的限制且航线也相对较短，达到了预期的效果。

图6 地形影响下规划的航线

4 结束语

图7 地形、防空火炮影响下的航线

图8 地形、雷达探测影响下的航线

图9 各因素综合影响下的航线

航线规划问题是近年来航空科学领域研究的重点，但是针对直升机低空突防的三维航线规划的研究却相对缺乏。本文在对空间区域进行栅格化处理的基础上，综合考虑地形、雷达探测、防空火炮威胁以及直升机自身性能的影响，提出了一种专门面向直升机低空突防的三维航线规划算法。基于邻域搜索策略和回退策略生成一条可以避开所有障碍的栅格路径 进而进行简化 顾及直升机自身性能限制和障碍的分布提取关键转折点，连接各转折点最终得到规划的航线。该航线避开了所有障碍、满足直升机自身性能的限制且航线也相对较短。仿真实验规划出了具有较高质量的航线，证明了该算法的可行性。

［1］ 符小卫，高晓光．一种无人机路径规划算法研究［J］．系统仿真学报，2004，16（1）：20－21．

［2］ 闵昌万，袁建平．军用飞行器航迹规划综述［J］．飞行力学，1998，16（4）：14－19．

［3］ 李霞，魏瑞，轩周军，等．基于改进遗传算法的无人飞行器三维路径规划［J］．西北工业大学学报，2010，28（3）：343－348．

［4］ 李婷，崔杜武．基于规则归纳的遗传算法选择和参数设置［J］．计算机工程，2010，36（3）：218－220．

［5］ WEI Dong，ZANCHETTA P．Tho mas P．Identification of Electrical Parameters in A Power Net work Using Genetic Algorith ms and Transient Measurements［J］．International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2010．29（1）：235－249．

［6］ 夏丛亮，张军良，刘海娟．遗传算法在低空突防中的应用［J］．无线电工程，2012，42（3）：57－60．

［7］ 刘丽峰，曲国庆，孔维华．利用动态规划和电势理论规划UAV三维航线［J］．计算机工程与应用，2013，49（20）：235－239．

［8］ 邱福生，杨建平，邵绪威．基于遗传模拟退火算法的无人机航线规划［J］．沈阳航空航天大学学报，2014，31（1）：16－19．

［9］ 杨富民，万刚，李锋．复杂战场电磁态势三维可视化研究［J］．测绘工程，2012，21（2）：35－38．

［10］张晓楠，任志国，曹一冰，等．交通运输最短路径分析系统的设计与实现［J］．测绘工程，2014，23（1）：25－30．

［11］何娟，涂中英，牛玉刚．一种遗传蚁群算法的机器人路径规划算法［J］．计算机仿真，2010，27（3）：170－174．