HyperFLOW软件数值模拟TrapWing高升力外形

赵 钟，赫 新，张来平，何 琨，何 磊

(1.中国空气动力研究与发展中心计算空气动力研究所，四川绵阳 621000; 2.空气动力学国家重点实验室，四川绵阳 621000)

HyperFLOW软件数值模拟TrapWing高升力外形

赵 钟1，*，赫 新1，2，张来平1，2，何 琨1，何 磊1

(1.中国空气动力研究与发展中心计算空气动力研究所，四川绵阳 621000; 2.空气动力学国家重点实验室，四川绵阳 621000)

采用High-Lift研讨会提供的梯形翼外形(TrapWing)，利用自主研发的基于结构、非结构网格的通用CFD软件HyperFLOW进行了数值计算，以评估其对复杂外形低速流的模拟能力。分别采用了三套不同拓扑结构的计算网格，包括两套非结构/混合网格和一套多块结构网格，每套网格又分为粗、中、细三种密度不同的网格数量以考察其网格收敛性。利用Richardson插值法，对计算结果开展了可信度分析。结果表明，不管是结构网格还是非结构网格，HyperFLOW均建立了可接受的可信度;对于高升力外形数值模拟，SA湍流模型要比SST湍流模型模拟的更准确;在失速迎角附近，现有的二阶精度解算器仍需持续改进。

HyperFLOW软件;梯形翼;高升力外形;验证与确认;计算流体力学软件

0 引言

随着计算流体力学(CFD)在航空航天飞行器设计中得到越来越广泛的应用，CFD计算结果可信度已成为CFD应用者关心的核心关键问题之一。从上世纪90年代开始，欧美国家组织举办了系列的CFD验证与确认活动(Workshop)［1］，其目的正是评估现有的CFD方法和软件对特定问题的模拟能力。在国内，飞行器设计部门出于对自身关心的流动问题模拟能力评估的考虑，以邀请多家协作单位参与相同任务的计算、召开数据对比会的形式，对特定流动速域飞行器标模开展了系列CFD数据的不确定度分析工作。与此同时，近年来，在国家重点基础研究发展计划(973)等项目的资助下，航空界组织开展了航空可信度研究活动，国内多家单位参与其中［2］。

对于大型运输机和民航飞机，高升力系统对飞行器的性能有很大影响［3］，因此高升力系统设计及其气动特性预测一直是航空界(尤其是民用飞机)的前沿课题。虽然利用CFD方法和软件预测真实飞行器气动性能的能力已基本获得飞行器设计师的认可，然而，对于高升力外形的数值模拟可信度水平仍然较低。高升力外形对CFD的挑战主要体现为流动现象的复杂性［4-5］:多段翼型产生的复杂缝隙效应，空间流场压力恢复效应，尾迹与边界层相互作用，大范围分离，翼稍涡卷起，层流湍流转捩等。以上因素的叠加，给高升力外形的CFD数值模拟带来了很大的困难。

为了评估当前CFD技术对高升力外形的预测能力，为工程应用提供经验指导，进一步提高高升力外形CFD预测的可信度，AIAA分别于2010年、2012年举办了两次高升力外形预测活动(AIAA High-Lift Prediction Workshop)［6-7］，他们选用了NASA梯形翼(TrapWing)构型作为主要研究对象。该活动吸引了全球多个国家和地区的CFD研究者参与并提交结果。为了便于参与者对自主发展的CFD软件进行确认，活动组织者提供了详细的风洞试验数据。国内先后开展的两期航空CFD可信度研讨活动也选取了该外形作为主要研究对象之一。

为了满足我国航空航天飞行器大规模CFD模拟的需求，作者所在的研究团队开发了一款同时适应于结构网格和非结构网格的通用CFD软件平台——HyperFLOW，利用系列标模对其进行了详细的测试。同时，作为主要参与团队，全程参与了国内航空CFD可信度研讨活动，为活动提供了一套非结构标准网格，并对自主研发的HyperFLOW软件进行了比较系统的验证与确认。

本文针对复杂低速流动问题，采用TrapWing高升力构型，分别基于结构网格和非结构网格，对HyperFLOW的低速流数值模拟能力进行了测试。基于Richardson插值方法，进行了网格收敛性研究，通过与试验结果对比，分析了计算结果的可信度。

1 HyperFLOW软件平台简介

HyperFLOW(Hybrid Platform for Engineering and Research of FLOWs)软件平台是在中国空气动力研究与发展中心自主发展的结构和非结构主力软件的基础上，独立开发的一款面向工程应用和学术研究的通用CFD软件平台。该软件借鉴了面向对象的大型软件设计理念，采用C++语言编程。为了适应结构网格、非结构网格和混合网格的计算，设计了具有良好通用性、可扩展性的体系结构和数据结构［8］;提出了“运行数据库”的概念，用于各类数据的管理和调用，实现了在同一软件平台上，结构解算器和非结构解算器的独立运行，并初步实现了结构解算器和非结构解算器的同步耦合计算［9-10］。下文开展的数值计算仅针对结构解算器和非结构解算器。

HyperFLOW的核心计算模块采用二阶精度的格心型有限体积方法。无粘项通量计算集成了Roe、Vanleer、AUSM、Steger-Warming等格式;通过梯度重构得到二阶精度的物理量分布。为了抑制激波附近的振荡、保持单元内物理量分布的单调性，集成了多种限制器。粘性项采用中心格式计算，而湍流效应通过“松耦合”湍流模型方程的形式进行求解。目前已集成了SA一方程湍流模型［11］和SST两方程湍流模型［12］，以及相关的改进模型;湍流模型方程本身的计算与N-S方程的求解类似。时间离散集成了显式Range-Kutta、隐式LU-SGS方法。为了适应大规模工程计算的需求，两种解算器均发展了基于网格分区的大规模并行计算技术。关于该软件的设计思想和研究进展，请参见文献［8-10］。

2 TrapWing高升力外形及计算网格

2.1 TrapWing高升力外形

计算采用的高升力外形是NASA梯形翼外形。该外形是安装在机身上的大弦长、半展、三段构型，机翼无扭转、无上反角。High-Lift活动中要求对襟副翼折转角分别为20(构型8)和25(构型1)度的两个外形进行计算，本文只针对构型1进行计算。

该外形的风洞试验是1998年在NASA Langley 14×22英尺亚声速风洞中完成的，其试验条件为［13］:马赫数Ma=0.2，雷诺数Re=4.3×106。试验时，机身固连于垫块，垫块安装于风洞壁，在CFD计算时，垫块气动力也计入总气动力。图1为几何外形，表1是外形几何参数和参考尺寸。

图1 TrapWing高升力外形试验照片Fig.1 The geometry of NASA trapezoidal wing

表1 TrapWing外形几何尺寸Table 1 Geometric details of trapezoidal wing model

2.2 计算网格

参考AIAA High-Lift研讨会的做法，分别采用粗、中、细三种不同数量的网格进行计算。计算中，选用了三套不同拓扑结构的网格，即:Grid1是AIAA HighLift-I Workshop中提供的非结构网格UH8(Unst-Mixed-Node centered-B，图2(a))，由德国宇航院DLR的网格生成软件SOLAR生成［14］，物面是三角形/四边形混合网格，空间是以六面体为主、掺杂了四面体/三棱柱/金字塔的混合网格填充;Grid2是自主生成的三棱柱/金字塔/四面体组成的混合网格(图2(b))，生成过程是首先采用全四面体网格填充空间，其中物面附近为各向异性四面体而外场为各向同性四面体，然后采用HyperFLOW软件的预处理模块将各向异性四面体网格聚合成三棱柱/金字塔网格［15］;Grid3是多块结构网格(图2(c))，粗中细网格分别为355、369、369块，该网格是第二届航空可信度活动提供的标准多块结构网格。

三套网格单元数见表2，其中Grid1的细网格单元量数达到1.4亿，而Grid2的细网格仅0.28亿，原因是在生成Grid2物面网格过程中，对具有不同流场特征的局部分别采用了不同拉伸度的三角形，如在机翼前后缘处，采用了展向大拉伸度的各向异性三角形填充，在保证网格分辨率的同时使得网格量大大减少。

图2 三套计算网格中的中等网格Fig.2 Three types of computational grids(medium)

表2 TrapWing外形计算网格量Table 2 Cell number of trap wing

3 计算结果分析方法:Richardson插值法

CFD的验证过程主要有两种手段［1］，其一是与精确解(解析解)或者制造解比较，如运动等熵涡和Couette流算例等。而对于复杂问题，一般采用网格收敛性方法结合Richardson插值法进行。众多学术期刊的编辑方针都认为严格定义的网格细化或粗化研究是计算结果精度评估的一种有效措施，由于不可能对网格进行无限制地加密，因此要求作者尽可能的结合Richardson外插方法来判断数值解的收敛性以及实际的计算精度。

Richardson方法主要是通过对不同密度网格的计算结果进行插值，估算出当网格量趋于无穷时的值。对于两套网格计算结果，一般Richardson外插法求解过程为［16-17］:

式中，f是所要分析的变量，如升力、阻力、力矩系数，fexact是插值结果，以此代表当网格量趋于无穷大时的解。p是网格解收敛精度，二阶精度格式该值为2。εi，j是由网格i与网格j计算所得解之差，即 εi，j=fi-fj，ri，j是网格细化比，ri，j=hj/hi，h= NTFS-1/3，NTFS是求解的未知量个数，格心型方法是单元数量，格点型方法是网格点数量。

对于粗、中、细三套网格，当计算结果单调时，式(1)中的p满足如下方程:

式中，下标1、2、3分别表示细、中、粗网格，p由迭代计算获得，如二分法、数值迭代法等。这里rij和εij的含义和上文一致。

4 计算结果分析

根据AIAA High-Lift Prediction Workshop提供的计算状态，采用两个Case分别考察HyperFLOW的网格收敛性和计算精度。在没有特殊说明的情况下，计算采用SA一方程湍流模型，Roe通量格式和Vankatkrishnan限制器，时间离散采用LU-SGS隐式格式。

4.1 Case1:网格收敛性研究

该状态的计算条件为:马赫数Ma=0.2，雷诺数Re=4.3×106(基于平均气动弦长)。采用粗、中、细网格，分别计算迎角为13°和28°时的气动特性，进行网格收敛性研究。

图3是迎角分别为13°和28°时，气动力系数随网格密度的收敛图，图中横坐标N表示网格单元数，若收敛过程表现为直线，则说明解算器的网格收敛性具有二阶精度［4-5］。从计算结果看，Grid1和Grid2均具有可接受的网格收敛性，随着网格的加密，逐渐趋向于实验值，收敛过程近乎直线，说明具有较好的收敛性;而Grid3在13°迎角时，单调性、收敛性不如非结构网格;同时，从图中给出的粗、中、细网格Richardson插值结果看，13°时的力矩系数插值结果与实验值有一定偏差，其他结果和实验值符合较好，表明计算结果具有较好的可信度。从网格收敛精度看，HyperFLOW的结构解算器计算结果比非结构解算器稍差。

为分析高升力外形的复杂气动力特性，有必要研究其物面压力分布情况。AIAA高升力预测活动中提供了多个展向站位的压力分布数据，HyperFLOW的计算结果除28°迎角、98%站位外，其他状态的结果与实验值均符合较好，由于篇幅所限，这里只给出了13°、85%站位的压力分布(图4)。由于后缘襟翼(flap)在该站位时存在展向和弦向的复杂分离流动，因此该处对网格分布极为敏感，可以看到三套网格都表现了很好的网格收敛性。相较于Grid1和Grid3，Grid2的粗网格计算结果在该处偏低，是因为其网格量仅有547万，也说明了对于具有复杂流动的局部，需要有合理的网格分布、网格量，才能正确模拟物理现象。实际上，对于13°、28°迎角时的其他大部分站位，压力分布都与上述情况类似:随着网格的加密，逐渐逼近于实验值。

图3 气动力系数的网格收敛性Fig.3 Grid convergence characteristic of aerodynamic coefficients

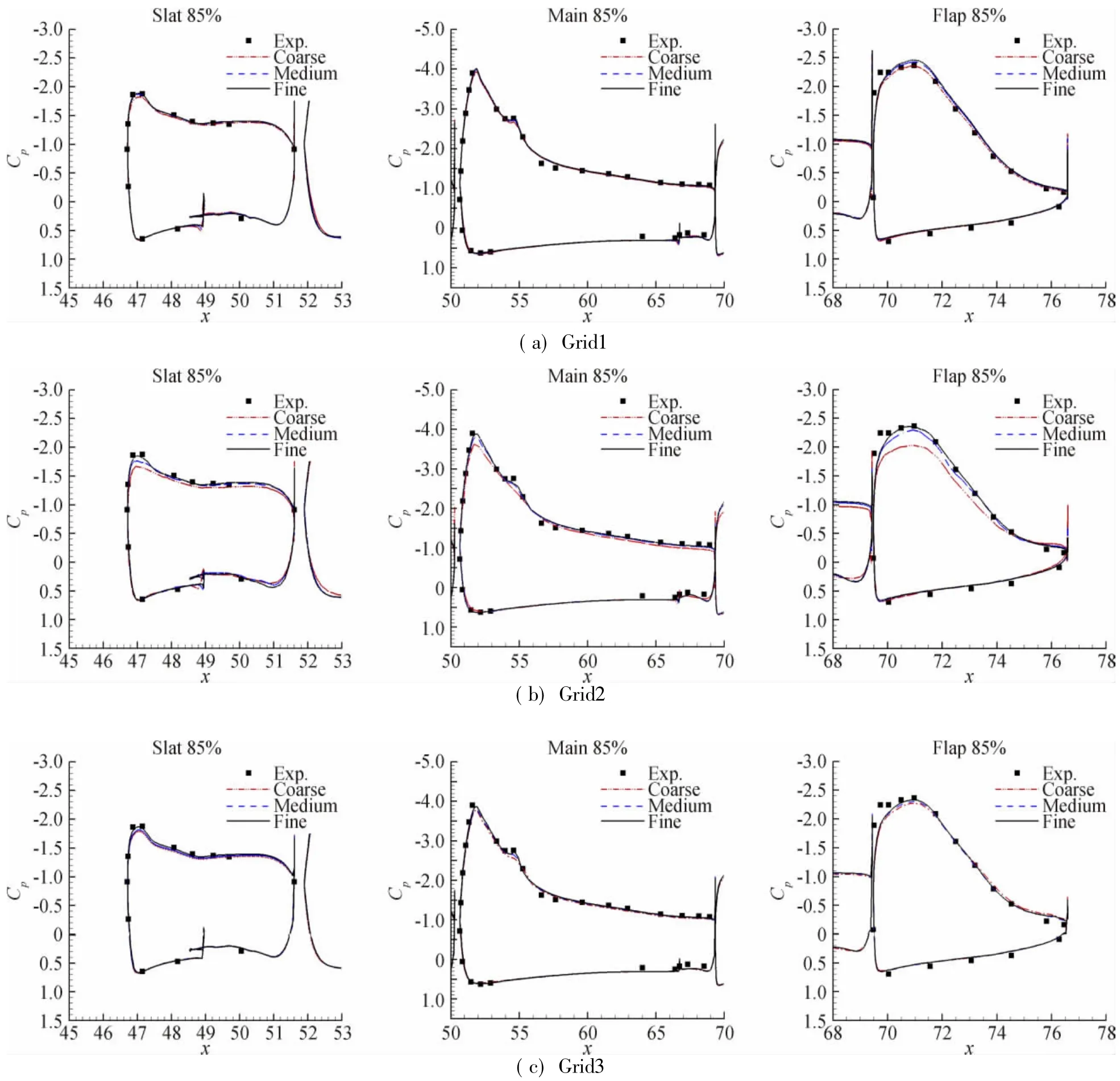
图4 三套网格物面压力分布对比:α=13°，85%站位Fig.4 Surface pressure coefficients at 85%span station，α=13°

在High-Lift Workshop中，迎角28°时98%站位处因存在复杂流动现象，压力分布难以精确模拟，是对CFD代码性能的重要挑战［4-5］，图5是三套网格在该状态下的站位压力分布比较。总体来看，三套网格均表现了很好的网格收敛性，粗网格与实验值差异最大，细网格与实验值吻合较好。而对于flap翼，由于同时存在背风区大分离和翼稍涡的卷起，使得该处的流动状态难以精确模拟，数值模拟的前缘压力峰值偏小，吸力偏低，从而导致总升力偏低，这也是计算的升力普遍比实验值小的原因。图6是HyperFLOW软件非结构解算器(Grid1)与Workshop中提交的两个典型结果的比较，二者分别是提交结果分布的两条边界曲线，可见，HyperFLOW软件模拟的压力分布比较接近上限曲线，具有较好的可信度。实际上，该站位位于翼稍，在大迎角状态下，物面压力受多种因素的共同作用，如湍流转捩、连接支架、气动弹性变形等。文献［18-20］在采用了转捩模型、考虑了连接支架干扰后，与实验值更为接近。

4.2 Case2:计算精度研究

该状态的计算条件为:马赫数Ma=0.2，雷诺数w〗Re=4.3×106(基于平均气动弦长)，迎角是6°、13°、21°、28°、32°、34°、37°。该状态的目的是进行计算精度研究。

图5 三套网格物面压力分布对比:α=28°，98%站位Fig.5 Surface pressure coefficients at 98%span station，α=28°

图6 迎角28°时flap压力分布与其他软件比较Fig.6 Surface pressure coefficients compare

一直以来，高升力外形大迎角模拟是CFD软件面临的一大挑战，主要表现为对失速迎角、最大升力系数的模拟存在困难。在AIAA High-Lift Prediction Workshop以及国内航空可信度活动中，普遍存在难以进行大迎角精确模拟的问题，其中几个主要问题包括最大升力系数偏低、失速迎角与实验值符合不理想、大迎角时(大于28°)对初始流场设置比较敏感［4，14］、湍流模型影响较大等。作者在进行计算时，也发现了大迎角时对初值敏感的问题，因而采用了Workshop中的典型计算方法:即当迎角大于28°时，分别采用前一个状态的流场作为初场进行计算。

图7是气动力系数曲线与实验值(包括上下边界)、国外知名软件参考值［6］的比较。对于升力曲线，除了Grid2的粗网格外，线性段均模拟较好，说明要准确模拟高升力外形需要有足够的网格量。在失速

迎角附近区域，最大升力系数和失速迎角均落入Workshop中其他知名软件的范围中;对于阻力曲线，均表现了良好的网格收敛性，且与实验值、参考值有相当的吻合度，说明计算结果可信;对于力矩曲线，虽然都表现了良好的网格收敛性，随着网格加密逐渐趋向于实验值，但是不同密度的网格间分布散度较大，说明力矩模拟有较大的网格量需求。

在失速迎角附近，计算结果的散布较宽，而且在不同的网格上的计算结果有较大差异，说明对于失速迎角附近状态的计算可信度还有待提高，其主要原因是在大迎角时，流场中出现了大范围的分离流动，而二阶精度格式的RANS模拟对大范围分离流动的模拟能力还比较有限。

目前来说，采用RANS方程模拟真实飞行器是工程中的主要途径，但是对于复杂外形尤其是高升力外形，由于大范围分离、转捩等因素的影响，使得不同湍流模型对结果影响很大。图8分别给出了在结构网格(解算器)、非结构网格(解算器)上，SST湍流模型和S-A湍流模型对升力的影响:SST模型模拟的升力普遍偏低，而且工程师比较关注的最大升力系数、失速迎角均与实验有较大差异。究其原因，从图9可见(Grid3，结构解算器)，SST模型模拟的主翼上翼面吸力要比SA模型小得多，从而导致升力系数偏低。这一结论与AIAA High-Lift Prediction Workshop的统计结果一致［4］。

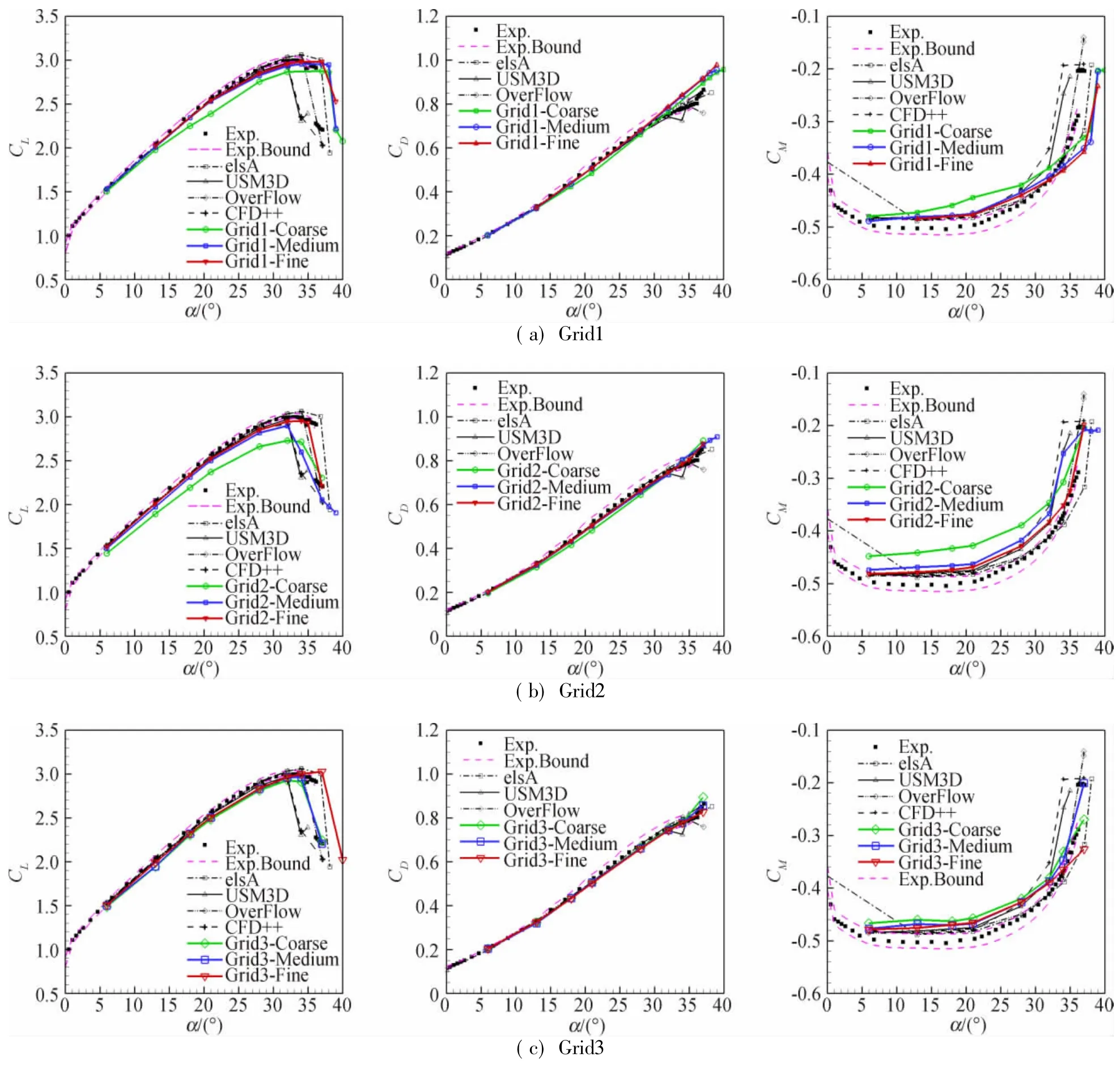
图7 气动力系数曲线Fig.7 Lift，drag，moment coefficient curves

研究过程中同样发现了大迎角时初场对计算结果影响较大的问题:图10是Grid2中等网格采用SA湍流模型计算时，大迎角(大于28°)状态分别以均匀来流和相邻小迎角状态收敛流场作为初始流场，所计算得到的升力。可见，若大迎角状态以均匀来流作为初场，会出现提前失速的现象。不仅如此，文献［22］中提到，对于类似的两段翼型做低速实验时，也存在类似的现象，文中将之用“迟滞效应”来解释。

图8 湍流模型对升力的影响Fig.8 Effects of turbulent models on lift

图9 湍流模型对物面压力系数的影响Fig.9 Effects of turbulent models on pressure coefficient

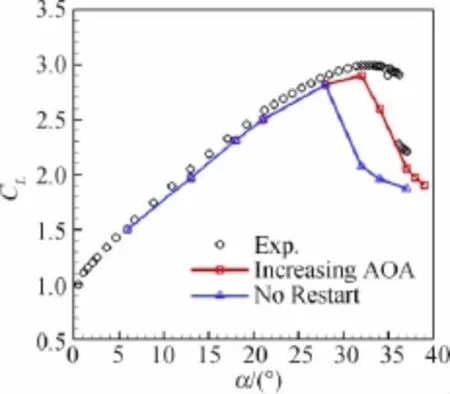
图10 大迎角时初值对升力系数的影响Fig.10 Effects of initial flow on lift coefficients

5 结论与展望

从本文的数值计算结果及网格收敛性分析可以看出，对于以高升力外形为代表的航空飞行器数值模拟，HyperFLOW软件对以附着流为主要特征的复杂外形的数值模拟具有良好的网格收敛性和计算精度。整体而言，计算结果具有较高的可信度，精度与国外知名In-House软件相当，基本能够满足航空飞行器高升力外形对CFD数据的需求。但与国外的一些著名软件类似的是，对失速迎角、最大升力系数的模拟还不够精确，其主要原因是涉及大范围的流动分离，未来需要在这方面进行持续改进。

就高升力装置数值模拟中的相关问题，我们通过前述的数值模拟，总结提出如下建议:

(1)湍流模型对于高升力装置的模拟非常关键。对比计算了SA模型和SST模型后，得出了与High-Lift Workshop一致的结论，即SA模型的计算结果优于SST的计算结果。因此，对于高升力外形的数值模拟，建议采用SA湍流模型，同时采用高分辨率的计算格式(如Roe格式)，不加限制器或者尽量减小限制程度。

(2)计算网格依然是得到高精度计算结果的关键。高升力外形对计算网格有强烈的依赖性，尤其是对大迎角状态，不同计算网格间有较大的差异。建议在生成网格时，采用AIAA High-Lift Prediction Workshop给出的网格生成指导原则，如机翼前后缘网格的长度、边界层内网格的法向正交性、第一层网格高度、网格法向增长比率、机身前后缘网格尺度、网格分布的光滑性等。同时，要采用不同密度的网格进行网格收敛性测试。

(3)初场设置对失速特性有较大影响。由于存在流动分离现象，初始扰动对于大迎角时的分离形态有较大影响，一旦出现流动分离结构，很难通过迭代计算改变流动结构。这一现象在High-Lift Workshop中也得到印证。因此，对于大迎角状态，建议将相邻小迎角收敛流场作为初场，以便更好地预测失速迎角。出现这种现象的原因到底是什么?目前仍需深入研究。

(4)几何外形的真实模拟是改进计算结果的有效途径之一。真实的TrapWing模型中，三段机翼之间还带有连结支架(brackets)，本文计算时没有考虑该装置。另外，真实外形还带有气动弹性效应。以上两个因素导致计算几何模型的变化，而这种变化会对计算结果产生影响，尤其是气动弹性变形导致的翼梢变形将改变局部的流动形态，进而影响压力分布，这可能是目前的计算所得压力分布与实验偏差较大的主要原因之一。而High-Lift Workshop后续研究工作表明，考虑连接支架和气动弹性的影响有助于改进计算结果的精度。因此，以后的工作中应该加以考虑。

(5)采用高级的湍流模型和高阶精度计算格式是未来的发展趋势。高升力外形的大迎角状态，尤其是失速迎角附近，背风区及翼稍附近存在复杂的流动分离现象，目前工程应用中广泛采用的RANS模拟方法还难以精确模拟，未来需要采用脱体涡模拟(DES)或大涡模拟(LES)等高级湍流模拟方法，并采用高阶精度的计算格式。

总之，尽管目前对于复杂构型的CFD数值模拟已取得长足的进展，但是仍局限于以附着流占主导地位的流动数值模拟，对于复杂分离流、旋涡运动等现象的数值模拟，仍有很长的路要走，除了发展更适用的物理模型、计算格式和网格技术外，全面系统深入的验证与确认必不可少，这将是CFD方法研究和软件研制永恒的主题之一。

致谢:本文使用的Grid3结构网格是第二届国内航空可信度活动的标准结构网格，由空气动力学国家重点实验室王运涛博士、李松博士提供。同时，在开展软件的验证与确认过程中，得到了中国空气动力研究与发展中心张益荣助理研究员的帮助，在此一并表示感谢。

［1］Deng Xiaogang，Zong Wengang，Zhang Laiping，et al.Verification and validation in computational fluid dynamics［J］.Advances in Mechanics，2007，37(2):279-288.(in Chinese)邓小刚，宗文刚，张来平，等.计算流体力学中的验证和确认［J］.力学进展.2007，37(2):279-288.

［2］流体中文网.http://www.cfluid.com/bbs/

［3］Zhu Ziqiang，Chen Yingchun，Wu Zongcheng，et al.Numerical simulation of high lift system configuration［J］.Acta Aeronautica et Astronautica Sinaca，2005，26(3):257-262.(in Chinese)朱自强，陈迎春，吴宗成，等.高升力系统外形的数值模拟计算［J］.航空学报，2005，26(3):257-262.

［4］Rumsey C L，Slotnick J P，Long M，et al.Summary of the first AIAA CFD High-Lift prediction workshop［J］.Journal of Aircraft，2011，48(6):2068-2079.

［5］Rumsey C L，Long M，Stuever R A.Summary of the first AIAA CFD High Lift prediction workshop［R］.AIAA 2011-999.

［6］1st AIAA CFD high lift prediction workshop.http://hiliftpw.larc. nasa.gov/index-workshop1.html/

［7］2nd AIAA CFD high lift prediction workshop.http://hiliftpw.larc.nasa.gov/

［8］He Xin，Zhao Zhong，Zhang Laiping，et al.Research of general large scale CFD software architecture and data structure［J］.Acta Aerodynamica Sinica，2012，30(5):557-565.(in Chinese)赫新，赵钟，张来平，等.大型通用CFD软件体系结构与数据结构研究［J］.空气动力学学报，2012，30(5):557-565.

［9］He X，Zhao Z，Zhang L P.The research and development of structured-unstructured hybrid CFD software［J］.Transactions of Nanjing University of Aeronautics＆ Astronautics，2013，30(sup):116-126.

［10］He Xin，Zhao Zhong，Zhang Laiping.The research and development of structured-unstructured hybrid CFD Software HyperFLOW［C］//The proceedings of the 15th Chinese CFD Conference，Yantai，Shandong:2012.(in Chinese)赫新，赵钟，张来平.结构非结构耦合计算CFD软件HyperFlow初步验证［C］//第15届全国计算流体力学会议论文集，山东烟台:2012.

［11］Spalart S R.A one-equation turbulence model for aerodynamic flows［R］.AIAA-92-0439，1992.

［12］Wilcox D C.Reassessment of the scale-determing equation for advanced turbulence models［J］.AIAA Journal，26:1299-1310，1988.

［13］Judith A H，Anthony E W，Luhter N J.Trapezoidal wing experimental repeatability and velocity profiles in the 14-by 22-Foot subsonic tunnel［R］.AIAA 2012-0706.

［14］Simone C，Stefan M W.DLR contribution to the first high lift prediction workshop［R］.AIAA 2011-938.

［15］Zhao Zhong，Zhang Laiping，He Xin.Hybrid grid generation technique for complex geometries based on agglomeration of anisotropic tetrahedrons［J］.Acta Aerodynamica Sinica，2013，31(1):34-39.(in Chinese)赵钟，张来平，赫新.基于各向异性四面体网格聚合的复杂外形混合网格生成方法［J］.空气动力学学报，2013，31(1):34-39.

［16］Roy C J.Grid convergence error analysis for mixed-order numerical schemes［R］.AIAA 2001-2606.

［17］Chen Jianqiang，Zhang Yirong.Verification and validation in CFD based on the Richardson extrapolation method［J］.Acta Aerodynamica Sinica，2012，30(2):176-183(in Chinese)陈坚强，张益荣.基于Richardson插值法的CFD验证与确认方法的研究［J］.空气动力学学报，2012，30(2):176-183.

［18］Peter E，Ardeshir H，Shia H P.Influence of transition on high-lift prediction for the NASA trap wing model［R］.AIAA 2011-3009.

［19］Anthony J S，Jeffrey P S，John C V.Extended OVERFLOW analysis of the NASA trap wing wind tunnel model［R］.AIAA 2012-2919.

［20］Eliasson P，Peng S H，Hanifi A.Improving the prediction for the NASA high-lift trap wing model［R］.AIAA 2011-867.

［21］Wiart L，Meunier M.Computational assessment of the HiLifPW-1 Trap-Wing model using the EISA CFD software［R］.AIAA 2011-865.

［22］Kasim B，Glen W Z.Hysteresis effects on wind tunnel measurements of a two-element airfoil［R］.AIAA-93-0646，1993.

Numerical research of NASA high-lift trap wing model based on HyperFLOW

Zhao Zhong1，*，He Xin1，2，Zhang Laiping1，2，He Kun1，He Lei1
(1.Computational Aerodynamics Institute of China Aerodynamics Research and Development Center，Mianyang 621000，China; 2.State Key Laboratory of Aerodynamics，Mianyang 621000，China)

Up to date，simulation of subsonic flows over the high lift device is still a challenge，especially for the cases with higher angles of attack.In order to evaluate the ability of HyperFLOW，an inhouse CFD software for subsonic turbulence flow over complex geometries based on structured and unstructured grids，the NASA high lift trap wing model is selected and investigated.Two cases discussed in the NASA high-lift workshop are considered on three types of grids，i.e.two unstructured or mixed grids，and one multi-block structured grid.The simulations on coarse，medium and fine grids for each type are carried out to access the performance of grid convergence.The numerical results are analyzed using Richardson extrapolation method，and compared with the experimental data and the results by other famous CFD codes in the world.The comparison demonstrates that HyperFLOW has a good property of grid convergence on different grids.As the statistical conclusions of the NASA high-lift workshop，the numerical results are acceptable within the linear part of the aerodynamic forces in the regime of lower and medium angles of attack.However，it is still a challenge for the prediction of the cases in higher angles of attack，especially for the cases near stall.

HyperFLOW software;trap wing;high lift configuration;verification and validation; CFD software

V211.3

:Adoi:10.7638/kqdlxxb-2014.0026

0258-1825(2015)05-0594-09

2014-04-21;

:2014-08-25

国家自然科学基金(11272339)

赵钟*(1986-)，男，四川宜宾人，助理研究员，博士研究生.研究方向:非结构网格生成、CFD软件开发.E-mail:bell_cardc@163.com

赵钟，赫新，张来平，等.HyperFLOW软件数值模拟TrapWing高升力外形［J］.空气动力学学报，2015，33(5):594-602.

10.7638/kqdlxxb-2014.0026 Zhao Z，He X，Zhang L P，et al.Numerical research of NASA high-lift trap wing model based on HyperFLOW［J］.Acta Aerodynamica Sinica，2015，33(5):594-602.