多天线GPS姿态求解及误差分析
2015-03-27解放军理工大学通信工程学院卫星通信与导航江苏高校协同创新中心柯明星童凯翔
解放军理工大学通信工程学院 卫星通信与导航江苏高校协同创新中心 朱 明 吕 晶 柯明星 童凯翔
0 引言
GPS刚开始主要是用于授时及精密定位,随着载波相位差分技术及计算机技术的发展成熟,由多个GPS天线组成的载体姿态测量系统可以对载体姿态进行实时或事后的测量[1][7]。姿态在陆地、航海、航空及空间应用中都是非常重要的导航信息,尤其随着新技术的发展与革新,对姿态精度的要求越来越高,如航空重力测量、航空摄影测量等高精度测量技术需要达到事后分级甚至秒级姿态精度,航海、航空等领域一般要达到分级实时姿态精度。
目前,国内外许多学者对多天线测姿进行了大量的研究,根据天线布设的不同,提出了多种多天线姿态解算方法,其中最常用的有直接姿态求解算法和最小二乘姿态解算法。同时,也对影响多天线姿态解算精度的因素进行了相关分析,得到了一些有益的结论,如天线数量越多,基线越长,布设越均匀,姿态解算精度就越高。但是,由于载体范围的限制,天线布设很难满足理想的条件。因此,在有限的条件下,提高基线解算精度和寻找最优的姿态解算方法是非常关键的。本文通过比较当前常用的三种姿态求解算法其误差分析,认为在有限的条件下,提高基线解算精度和寻找最优的姿态解算方法是非常关键的。
1 多天线GPS姿态解算模型
1.1 本地坐标系
在确定姿态的时候,一般用地理坐标系当作参考坐标系。这个坐标系是建立在地心坐标系上,随着地球转动而转动。此坐标系定义为:以运动载体的质心为原点,沿着子午线向北,在地心矢量方向上,通过右手规则确定。本地坐标系如下图1所示,简称为ENU导航坐标系。

图1 本地坐标系
1.2 载体坐标系
一个载体的全姿态确定至少需要三个不在同一直线上的天线。为了不失一般性,载体坐标系xbybzb的原点选在主天线1上;xb轴沿原点指向天线2;yb轴垂直于天线平面;zb轴与xb轴和yb轴满足右手法则,且在天线平面内,如图2所示。
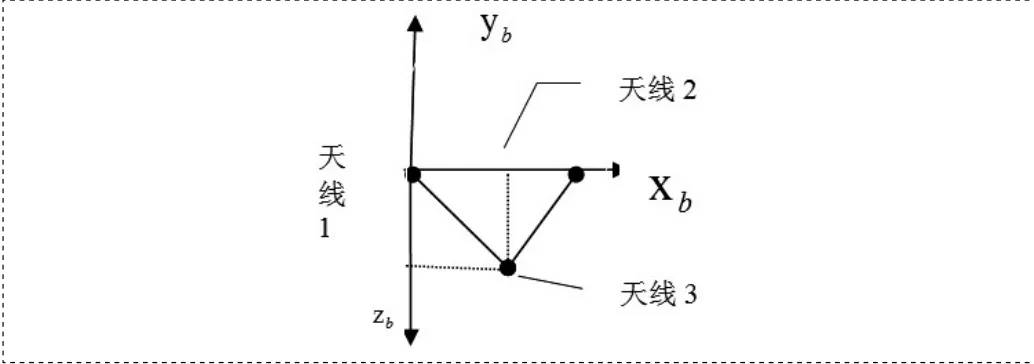
图2 载体坐标系
1.3 旋转矩阵
多天线姿态解算主要利用载体坐标系和本地坐标系之间的转换关系,对应的坐标系转换矩阵如下:
地心坐标系到本地坐标系的转换可以通过绕Ze正转入,然后再绕Ye反转(90°+L),最后绕XN反转90度就转换到了本地坐标系。
坐标转换矩阵为:
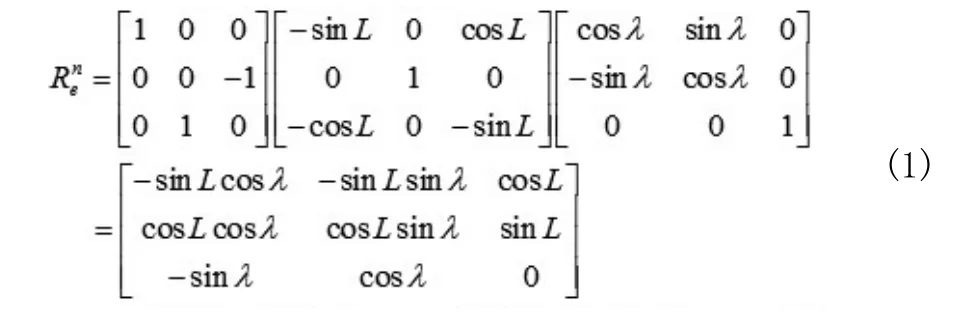
本地坐标系ENU通过偏航角 ,俯仰角 ,滚动角 转换到载体坐标系xbybzb,其对应的坐标转换矩阵如下:
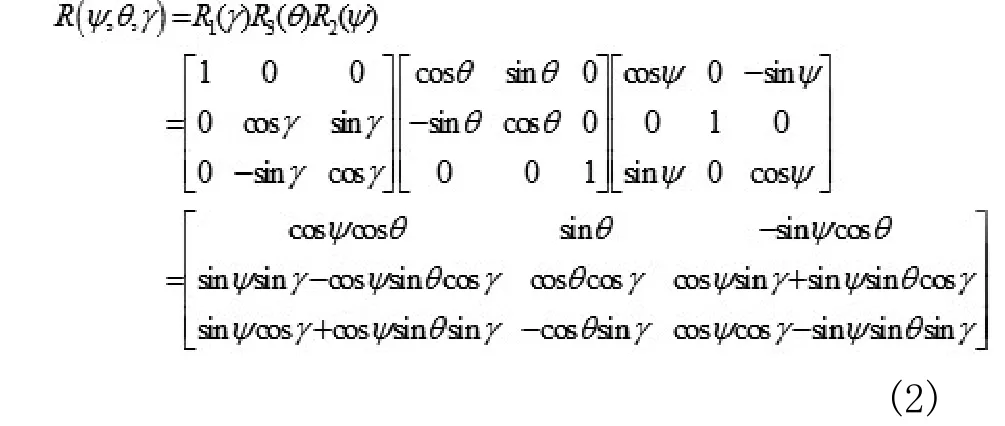
旋转角可以通过旋转矩阵元素R(i,j)表示如下:

本地坐标系到载体坐标系的旋转,实际上是把本地坐标系中的矢量(x,y,z)T映射成载体坐标系中的矢量(xb,yb,zb)T,可以写成:

2 姿态求解算法
利用GPS多天线求解姿态角的系统中,基线矢量的本地参考坐标系是通过GPS载波相位差分方程求得,参考坐标系的原点定义在主天线1上,而载体坐标系中的坐标被认为是精确已知的,且在动态过程中认为不变。
2.1 直接计算法1
GPS载体坐标系定义如图2所示。主天线1定为原点,天线1到天线2的基线b12定为x轴,则基线b12在载体坐标系下的坐标,b13的坐标为,而b12、b13在参考坐标系下的坐标分别为和。则姿态旋转矩阵 满足:

把基线矢量b12的坐标b12和u2代入(5)得:

又因为姿态矩阵是正交的,偏航角 和俯仰角 可求得如下:

观察上式可知,利用基线b12就可以确定用户的偏航角和俯仰角。当计算出偏航角和俯仰角之后,基线矢量b13经过如下变换:先绕y轴旋转,然后再绕旋转,从参考系旋转到辅助坐标系。b13在辅助坐标系中的坐标为:

由方程(9)可以解得旋转角 为:

直接计算姿态角公式仅用了当前历元的两个基线矢量,当超过两个基线矢量时,可以构成基线矢量对来求解姿态角。从统计的角度看,直接计算法是次优的,观察公式可看出没有用到。
2.2 直接计算法2
姿态旋转矩阵最为简单的求解方法是,利用两条不在同一直线上的基线构成天线平台,假定两条不共线的基线矢量在本地坐标系下的单位坐标矢量为u1和u2,在载体坐标系中的单位坐标矢量分别为b1和b2。当姿态矩阵R满足:时,利用u1和u2,构造成本地坐标系下的正交化矩阵:

同理,利用b1和b2构造成载体坐标系下的正交化矩阵:

使得旋转矩阵R为:

Mg和Ms都是3×3的正交矩阵。很容易求得姿态角旋转矩阵:

假如姿态旋转矩阵解出,根据(3)式可求解姿态角。此方法易理解且计算量较小,计算旋转矩阵R时不需要求逆,唯一的要求就是两基线矢量不共线。但是该方法从统计的角度看同样是次优的,因为仅用到两基线矢量的部分信息,且只用了一次。
2.3 最小二乘姿态估计
由(3)式可知,由三个旋转姿态角就能确定旋转矩阵,三个姿态角即为偏航角、俯仰角和滚动角。当基线矢量在载体坐标系中的坐标已知,那么根据方程(4)做最小二乘姿态估计就能确定。设和分别为天线i在载体坐标系和本地坐标系中的坐标,由此得:

其中n为从天线的个数。在方程(15)中,bi和ui为观测值,且它们的协方差矩阵分别为 和 ,待求解的是方程中三个姿态角 。此模型为标准的隐式最小二乘校正模型,它的特点是在姿态估计过程中,载体坐标系中的坐标bi的协方差矩阵参与运算。方程式(15)相对于的线性化模型可表示为:

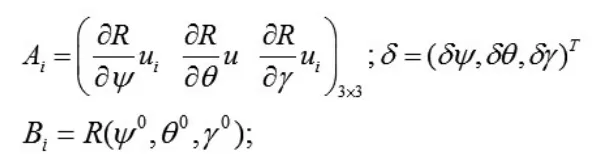
I为3×3的单位矩阵;



与直接姿态计算法相比,因为所有的定位信息都被采用,所以最小二乘姿态估计法是相对最优的,且还可以通过协方差矩阵直接求得姿态角的精度。最小二乘姿态估计的另一个优点就是受多径影响较小,这是因为最小二乘姿态估计最佳拟合了所有基线矢量[4]。
3 误差分析
对(7)式微分,忽略各坐标分量之间的相关性,再利用误差传递公式,则偏航角的标准误差可以表示为:
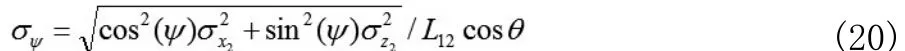
为了简化分析,认为各天线在本地坐标系下的各坐标分量的误差是独立同分布的[2],因此假设:

则式(20)可以简化为:

当前主流GPS载波相位测量定位技术的精度指标[8],水平方向可以达到 ,垂直方向精度为 。在GPS载波相位误差一定的情况下,影响偏航角误差的主要因素是基线的长度,基线越长,偏航角误差越小。此外俯仰角也是航向误差的一个影响因素,俯仰角绝对值越小,航向误差也就越小,俯仰角为零时航向误差最小。
同理,对(8)、(10)进行微分,同样利用误差传递公式,分别得到俯仰角和滚动角的误差公式如下:
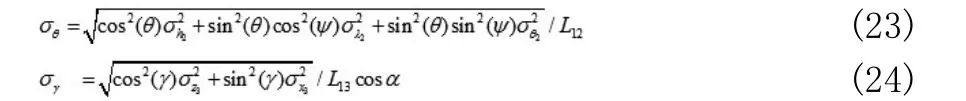
其中:

a是基线矢量b13和Xb轴的夹角。
俯仰角和滚动角近似表达式可以写为:

从式(25)、(26)观察易得到俯仰角的误差大小与定位误差大小成正比,与基线长度成反比。从式(24)、(26)可以看出,当两基线矢量互相垂直时,滚动角误差最小。
4 仿真结果
为了验证多天线姿态解算方法的正确有效性,利用Newstar210M多天线中频信号采样器实测数据进行检验,中频采样频率为16.367667MHz,信号带宽为2MHz,采集情景及天线安装位置如图3.数据采集于2015年5月2号于解放军理工大学通工楼楼顶。

图3 实验数据采集场景

测量这两条基线在载体坐标系下的基线矢量为:

由于两种直接计算方法结果等价,以下仅比较直接计算法一与最小二乘姿态解算结果。偏航角、俯仰角和横滚角估计结果见图4-6,误差估计结果见图7-9。

图4 偏航角估算值

图5 俯仰角估算值

图6 横滚角估算值

图7 偏航角误差估算值
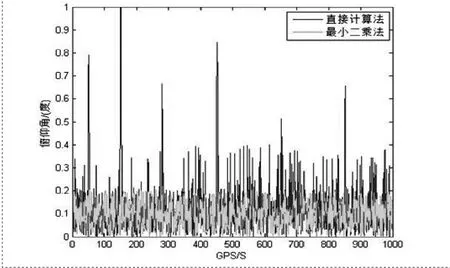
图8 俯仰角误差估算值

图9 横滚角误差估算值
分析图4-9可知。从估算误差来看,利用最小二乘算法的误差大小要明显优于直接计算法,这个结果是可以预见的,主要原因是最小二乘算法充分利用了所有的定位信息,而直接计算法仅仅用到两基线矢量的部分信息,所以是次优的。且姿态角精度与基线长度及天线模型有关。
5 结语
本文推导了三种常用的姿态解算方法的估计及其精度评定模型,对直接法和最小二乘解算的姿态结果及其误差进行了分析。仿真结果表明,最小二乘法对姿态角估算的确有改进。基于多天线阵的GPS观测数据可以对载体姿态进行测量,且多天线测姿精度受基线长度、基线精度、天线数量及天线分布等影响,在载体长宽有限、天线数量固定的情况下,为提高GPS测姿精度,可以合理布置GPS天线的相对位置,这也是下一步需要研究的问题。
[1]刘若普.GPS三维姿态测量技术研究[M].上海交通大学硕士学位论文,2008.
[2]Zhou Sanqi.Research on GPS-based Attitude Determination System for Degree of M.Eng of Beijing Jiaotong University,2009.
[3]Tian Xiang,Fan Shenglin Liu Jiangye.Research on Multibaseline Attitude System Based on GPS.Aerospace Control,26(2).
[4]唐康华.GPS快速定姿技术研究[M].国防科学技术大学硕士学位论文,2002.
[5]Chen Yulin.Study on Attitude Determination of Kinematical Carrier Using Carrier Phase of GPS System for the Degree of M. Eng of Nanjing University of Aeronautics and Astronautics,2005.
[6]Wanghai.Study of High Resolution DOA Estimation Algorithm and Its System Implement for the Degree of M.Eng of Wuhan Institude of Technology,2012.
[7]张守信.GPS卫星测量定位理论与应用[M].长沙:国防科技大学出版社,1996.
[8]何秀凤,刘建业.基于GPS载波相位的微卫星姿态算法研究[J].空间科学学报,2003,23(1):55-59.
[9]许江宁,朱涛,卞鸿巍.GPS 姿态测量技术综述[J].海军工程大学学报,2003,15(3):17-23.
[10]万德钧,李滋刚.GPS 航姿测量及其仿真研究[J].船舶工程,1996(4):62-78.
