移动无线传感器网络连通性自主恢复算法

马桂真，于 平

(1.北京联合大学 北京市信息服务工程重点实验室，北京100106;2.北京邮电大学 网络与交换技术国家重点实验室，北京100876)

0 引 言

无线传感器网络(WSNs)往往布置在无人值守的恶劣环境，节点容易发生故障，同时节点可能因电量耗尽而无法工作。网络中关键节点的故障会将无线传感器网络分割成多个不连通的分区，不同分区之间的节点无法协作完成任务，对网络性能产生严重影响。特别在战场和搜救应用中，人工很难干预，网络连通性的自主恢复非常重要。

移动无线传感器网络连通性恢复问题研究成为近年来研究的热点［1～8］，典型方法有PADRA［3］和DCR［7］。但是PDARA 方法中关键节点的确定需要确定网络的连通支配集(CDS)，能源消耗过大，且在连通性恢复过程中，可能会出现搜索路径过长的情况。DCR 方法出现过多不必要的“故障恢复”操作，造成无谓的能量消耗。

针对现存的问题，本文提出一种无线传感器网络连通性自主恢复策略，同时将算法进行了扩充，处理两个相邻节点同时故障的情况。

1 系统模型与假设

本文研究无线传感器网络的连通性自主恢复，问题可建模为求无向图的连通性问题。无向图G=(S，E)，其中，S={s1，s2，s3，…，sn}代表传感器节点集，E={(si，sj)|dis(si，sj)＜R}，dis(si，sj)表示节点si，sj之间的距离，R 表示节点的最大通信范围。网络中节点可按需移动，各节点之间通信范围都为R。本文还有如下的定义:

定 义1 1跳邻居:对于∀si∈S，∃sj∈S，若si和sj之间距离小于通信范围R，则sj是si的一跳邻居，记为N1(si)。

定义2 2 跳邻居:∀si，sj，Sk∈S，sj∈N1(si)，若sj和sk之间的距离小于R，且sk∉N1(Si)，则sk是si的2 跳邻居。

定义3 k 关键节点:∀si∈S，若去掉si其所有的k 跳邻居组成的子图是不连通的，则节点si是k 跳关键节点。

2 确定关键节点

获取本地信息多少与关键节点的确定存在一定的关系［9］，本文规定“2 关键节点”为关键节点。关键节点确定算法描述如下:

1)若节点n 是叶子节点，则n 是非关键节点。

2)若节点n 不是叶子节点，则将n 的1 跳邻居基于位置顺时针排列{ns1，ns2，…，nsn}。

3)对于节点n 的任意两个相邻的1 跳邻居nsi，ns(i+1)，若dis(nsi，ns(i+1))≤R，则2 节点可直接通信。若所有相邻1 跳邻居节点之间是可直接通信，则节点n 是非关键节点，如图1 中节点G，F 和D。

4)若dis(nsi，ns(i+1))＞R，则n 的1 跳邻居之间可能会形成不连通的分区D1，D2，…，Dn，Di={nsi，ns(i+1)，…，ns(i+k)}，则算法检测任意两个分区是否可以合并成一个分区。如图1 中节点M 的1 跳邻居形成两个分区{H，N}和{L，I}，但是两分区中N 和L 可直接通信，所以，两个分区可以合成一个分区，节点M 是非关键节点。

5)若步骤(4)执行完后至少有两个分区不能合并，则节点n 是1 跳关键节点。如图1 中节点A，1 跳邻居分布在{C，E}和{D，B}，且两分区之间没有节点可直达，则A 是1 跳关键节点。

6)若节点n 是1 跳关键节点，则检测任意两个分区中节点是否有相同的1 跳邻居(n 的2 跳邻居)，若存在，则这个二分区也合并为一个分区。若所有分区都合并为一个分区，则节点n 是非关键节点，否则，是关键节点。如图1 中节点A 的邻居形成的两个分区{E，C}和{D，B}中若任意两个节点B 和C 有相同的1 跳邻居L(L 是A 的2 跳邻居)，则节点A 是非关键节点。若节点L 与C 不可直接通信，则节点A 是关键节点。

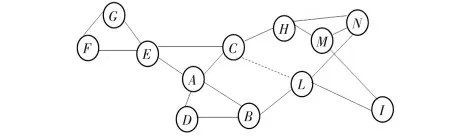
图1 关键节点识别算法Fig 1 Algorithm for critical nodes recognition

3 单个关键节点故障

3.1 备用节点确定

提前选取备用节点可以减少故障响应延迟，在时间要求严格的应用中尤其重要。本算法检测各级关键节点是否有非关键节点邻居，减少连通性恢复过程中的长搜索路径出现的几率。单个节点故障时备用节点选取算法如下:

Algorithm 1 Backupselect(S)

∥Backup(S)节点S 备用节点。

1)if critical(S)=true then

3) i=close(S，ileaf))∥最近的叶子节点

5) i=close(S，inon－critical)∥最近的非关键节点

8) i=close(S，ik)∥关键节点i 的最近的具有非关键节点邻居的关键节点邻居

10) i=close(S，i)∥最近的关键节点邻居

11) Backup(S)=i

备用节点确定以后，持续检测相应关键节点的状态。一旦发现关键节点故障，备用节点触发连通性恢复算法。

3.2 连通性恢复算法

关键节点n 的备用节点检测到n 故障，则触发连通性恢复过程，该过程包括非关键节点搜索和级联移动。搜索算法流程如下:

1)若备用节点是非关键节点，则搜索过程结束。

2)若备用节点不是非关键节点，则检查其备用节点是否非关键节点，若是，搜索过程结束;否则，重复步骤(1)，步骤(2)，直到找到非关键节点。

级联移动:搜索到非关键节点后，各节点级联向故障节点移动。如图2 中，若关键节点F 故障，其备用节点L 是非关键节点，则L 直接移动到F，即可恢复连通性。若K 故障，其备用节点E 也是关键节点，E 执行搜索算法，找到非关键节点G，节点G，E 向K 级联移动，恢复网络连通性。

图2 连通性恢复Fig 2 Connectivity recovery

4 相邻两个节点同时故障的情况

本文将APDCR 扩充，提出2—APDCR 处理两个相邻节点同时故障造成的网络不连通问题，仅考虑至少一个节点是关键节点的情况。

4.1 第二备用节点选择

针对两个相邻节点同时故障，备用节点选取标准如下:

1)两个关键节点不能相互为备用节点。

2)两个相邻的节点一个是关键节点，一个是非关键节点时:

a.若非关键节点不是关键节点的备用节点，则不需选择第二备用节点

b.若非关键节点是关键节点的备用节点，则从二者共同的邻居中选择第二备用节点，若没有共同邻居，则从关键节点的其他1 跳邻居中选择。选择标准同3.1 Algorithm 1。

3)两个相邻的节点都是关键节点时:

a.若二者有各自独立的备用节点，则不需选择第二备用节点:

b.若两相邻的关键节点中一个是另一个的备用节点，则需要选择第二备用节点，选择方法同步骤(2)中b。

4.2 连通性恢复

针对网络中两个节点同时发生故障的情况，有以下几种场景:

1)故障的两个相邻节点n1是关键节点，n2是非关键节点:

a.若n2不是n1的备用节点，则n1的备用节点直接移动到n1的位置即可恢复连通性。如图3 中关键节点M 和非关键节点N 同时故障，M 的备用节点I 移动到M 位置即可恢复网络连通性。

b.若n2是n1的备用节点，则第二备用节点检测到二者故障，开始连通性恢复过程。如图3 中关键节点L 及其备用节点R 同时故障，则第二备用节点X 开始非关键节点的搜索过程。找到非关键节点C，则X，C 向L 级联移动。

2)故障的两个节点n1，n2都是关键节点:

a.若n1，n2有各自独立的备用节点，且备用节点都是非关键节点，则各自平行移动到相应的故障节点即可恢复连通性。

b.若n1，n2有各自的备用节点，且备用节点一个是关键节点，一个是非关键节点，则非关键节点直接移动到关键节点位置。关键备用节点执行3.2 中非关键节点搜索算法找到非关键节点，然后向故障节点执行级联移动恢复网络连通性。

c.若n1，n2有各自的备用节点，且备用节点全部是关键节点，则两个备用节点都需要执行非关键节点搜索过程。借助文献［3］中防止冲突方式，搜索过程结束之前，搜索路径上所有节点先锁定，直到整个搜索过程结束。

d.若n2是n1的备用节点，则n2的备用节点和第二备用节点检测到故障发生，触发非关键节点搜索过程。如图3关键节点L 和其备用节点R 同时故障，R 的备用节点S 检测到R 故障，因为S 是非关键节点，则直接移动到R 位置即可;第二备用节点B 检测到节点R，X 检测到L 故障，搜索到非关键节点Q，然后Q，C，X 向L 级联移动。

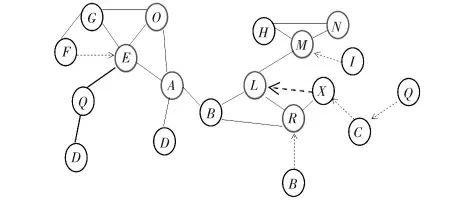
图3 2 节点故障连通性恢复Fig 3 Connectivity recovery for 2-node failure

5 仿真实验

本文通过一系列仿真实验验证算法的性能，在600 m×600 m 的正方形区域，随机生成连通网络。实验中设置网络中传感器节点个数分别为20，40，60，80 和100，节点通信范围从50，100，150 m 到200 m 变化。节点个数变化时，通信范围保持在100 m;通信范围变化时，网络中节点个数保持在60 个。对于相邻两节点同时故障情况，设置故障节点的任意一个1 跳邻居故障。每个拓扑执行30 次，取平均值作为实验结果。取移动节点个数和节点移动总距离作为性能指标，并与DCR 策略做比较，实验结果如图4～图7 中各图所示。

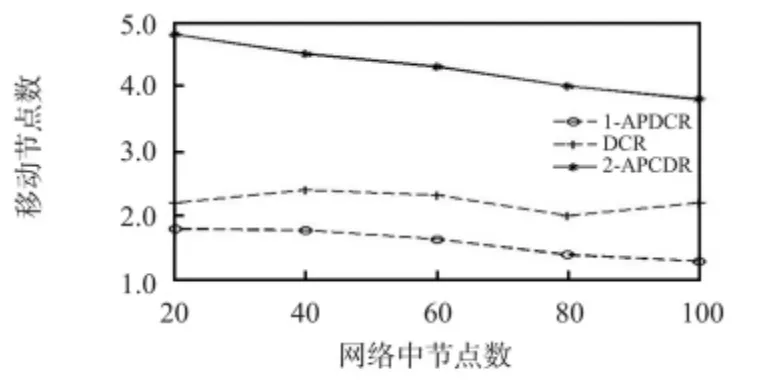
图4 网络节点数变化时移动节点数的变化Fig 4 Number change of mobile nodes with varying number of nodes in network

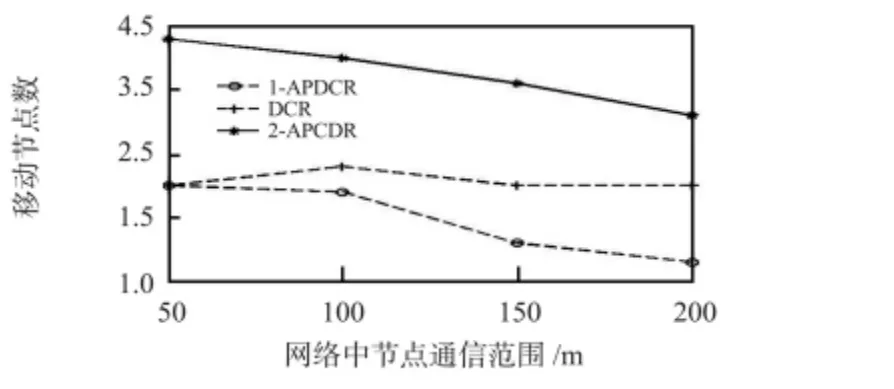
图5 网络通信范围变化时移动节点数变化Fig 5 Number change of mobile nodes with varying communication range of network

实验结果表明:1—APDCR 性能明显优于DCR(单节点故障)。这是因为1—APDCR 以2 跳关键节点作为关键节点，避免了处理过多“冗余”关键节点的可能，同时，1—APDCR 在选取备用节点时，限制了备用节点选取范围，从而降低了长搜索路径发生的几率，减少了移动节点的个数和节点总的移动距离，从而节省了节点能耗，延长了网络寿命。同时实验验证了2—APDCR 的可行性。

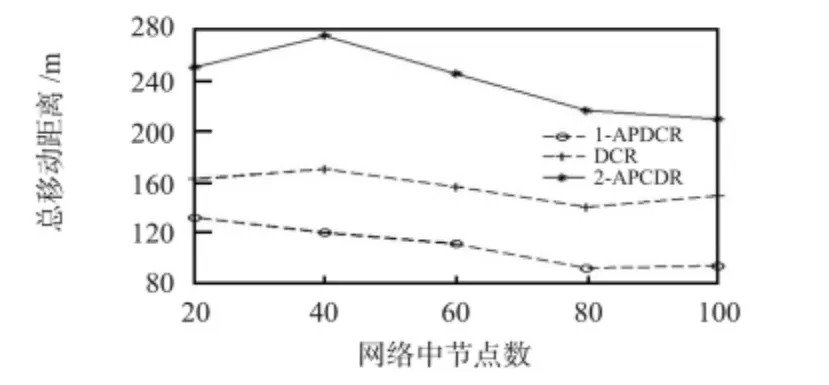
图6 网络节点个数变化时总移动距离变化Fig 6 Total change of moving distance with varying number of nodes

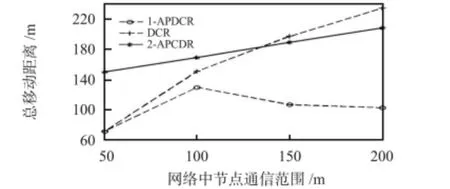
图7 通信范围改变时总移动距离Fig 7 Total change of moving distance with varying communication range

6 结 论

本文提出一种移动无线传感器网络连通性自主恢复策略，在保证网络连通性恢复的同时，算法设计重点考虑了算法的能耗。提出基于节点位置信息判别关键节点的算法，选取合适的备用节点，减少恢复过程中非关键节点的搜索范围。另外，算法可以处理两个相邻节点同时故障的情况。在后续的研究中，将进一步研究多节点同时故障时无线传感器网络连通性恢复问题。

［1］ Youns M，Senturk I F，Akkaya K，et al.Topology management techniques for tolerating node failures in wireless sensor networks:A survey［J］.Computer Networks，2014，58:254－283.

［2］ Senel F，Younis M.Relay node placement in structurally damaged wireless sensor networks via triangular steiner tree approximation［J］.Computer Communications，2011，34(16):1932－1941.

［3］ Akkaya K，Senel F，Thimmapuram A，et al.Distributed recovery from network partitioning in movable sensor/actor networks via controlled mobility［J］.IEEE Transactions on Computers，2010，59(2):258－271.

［4］ Younis M，Lee S，Gupta S，et al.A localized self－healing algorithm for networks of moveable sensor nodes［C］∥2008 IEEE Global Telecommunications Conference，2008 GLOBECOM，2008:1－5.

［5］ Tamboli N，Younis M.Coverage－aware connectivity restoration in mobile sensor networks［J］.Journal of Network and Computer Applications，2010，33(4):363－374.

［6］ Imran M，Younis M，Said A M，et al.Partitioning detection and connectivity restoration algorithm for wireless sensor and actor networks［C］∥2010 IEEE/IFIP 8th International Conference on Embedded and Ubiquitous Computing(EUC)，IEEE，2010:200－207.

［7］ Imran M，Younis M，Mdsaid A，et al.Localized motion－based connectivity restoration algorithms for wireless sensor and actor networks［J］.Journal of Network and Computer Applications，2012，35(2):844－856.

［8］ Senturk I F，Akkaya K，Yilmaz S.Distributed relay node positioning for connectivity restoration in partitioned wireless sensor networks［C］∥2012 IEEE Symposium on Computers and Communications(ISCC)，IEEE，2012:000301－000306.

［9］ Stojmenovic I，Simplotryl D，Nayak A.Toward scalable cut vertex and link detection with applications in wireless Ad Hoc networks［J］.Network，IEEE，2011，25(1):44－48.