基于DSP 的Fe83Ga17 合金磁致伸缩传感器信号处理系统设计*

王 展，周新志，雷印杰

(四川大学 电子信息学院，四川 成都610065)

0 引 言

磁致伸缩位移传感器利用了磁致伸缩材料的维德曼效应和维拉里效应［1］，具有高精度、大范围、强抗干扰能力的优点［2］，是一种非接触式的绝对位移测量传感器，目前已经被广泛应用到油库液位测量、水位监测、自动化等各个领域中［3］。传统的磁致伸缩位移传感器使用的材料受饱和磁致伸缩系数限制，其所产生的超声波在传播时衰减严重，无法被可靠地检测到，长距离应用受到了限制。

为了突破量程的局限，本文采用了一种具有更高磁致伸缩系数的Fe83Ga17合金，Fe83Ga17饱和磁致伸缩系数的增加不会以增加饱和磁场为代价［4］。传统的磁致伸缩信号处理基于硬件，而过多硬件电路会产生干扰，放大器的零点漂移和温度漂移也会对测量带来一定影响［5］。相对于单片机，数字信号处理器(DSP)体积和功耗更小，减少了系统硬件电路数量，其高速数据处理能力减少了A/D 转换时间，大大提高了转换精度。同时，本文针对温度对扭转波速的影响，设计了一种温度补偿方法，减小了误差，提高了测量精度。

1 磁致伸缩位移传感器原理

1.1 磁致伸缩位移测量原理

磁致伸缩位移传感器由磁致伸缩波导丝、接收线圈、激励电路、信号处理电路等组成，原理图如图1 所示。

波导丝加上脉冲电流Ip时，附近产生环形磁场Фi，固定磁铁产生轴向磁场Фm，Фi和Фm合成磁场Ф［6］。根据磁致伸缩效应，Ф 附近产生一个形变，进而产生一个弹性波，以固定速度v 向波导丝两端传播。当弹性波到达波导丝末端的接收线圈时，磁通量密度B 发生变化。根据法拉第电磁感应定律，设接收线圈匝数为N，磁致伸缩线横截面积为S，接收线圈上产生感应电压e 表示为［7，8］

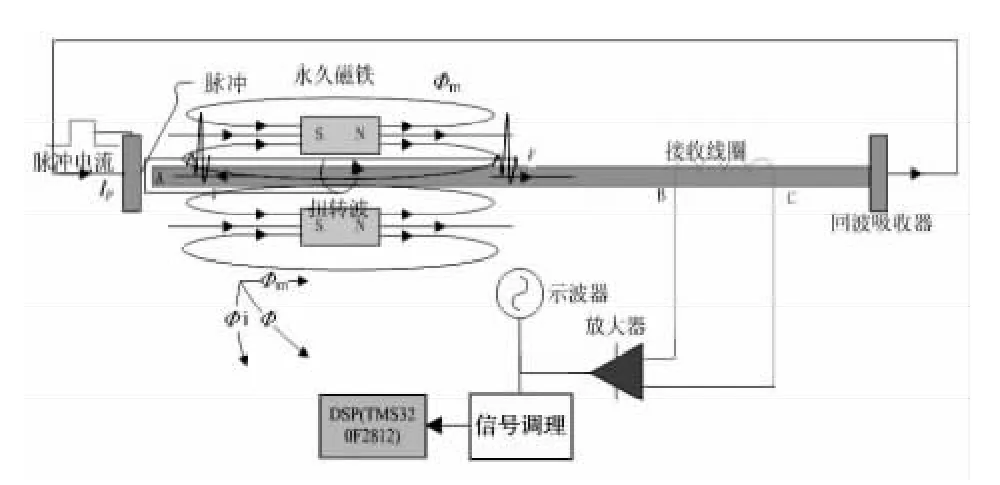
图1 磁致伸缩位移传感器测量原理图Fig 1 Principle diagram of magnetostrictive displacement sensor

如果弹性波的传播速度为v，从固定磁铁到接收线圈的传播时间为t，那么固定磁铁和线圈的位移L 可以表示为［9］

式中 v 为扭转弹性波的速度，G 为波导管的剪切弹性模量，ρ 为波导管密度，G 与ρ 在温度固定时恒定，因此，扭转弹性波的传播速度也是固定的。

1.2 Fe83Ga17材料特性

在磁场强度为H 的磁场中对Fe83Ga17进行磁化，磁感应强度B 不是关于H 的单值函数。随着H 增加，B 最终达到饱和，H 逐步减小时，B 的变化滞后于H，偏离了起始磁化曲线。当H 减小至零时，B 等于剩余磁感应强度Br。为使B 减小到零，需要施加一个称为矫顽力Hc的反向磁场。磁性材料中磁感应强度与磁场强度的关系是一条闭合线，称为磁滞回线［5］。Fe83Ga17磁致伸缩波导丝相关参数:直径为1 mm;剩余磁感应强度Br为0.007 T;饱和磁感应强度Bm为1.472 T;矫顽力Hc为1.4 kA/m。

根据Fe83Ga17新型材料磁特性的相关参数可知，Fe83Ga17材料具有磁导率大、矫顽力小、容易磁化和退磁、磁滞损耗小等特点［5］。

2 硬件比较器测量方法

传统信号检测采用硬件比较器的方式，经过电压比较器的信号电压变为0/5 V 的TTL 电平。硬件比较器电路图如图2 所示。

这种电路的优点是排除了小幅度杂波的干扰，信号清晰。缺点是当干扰信号的幅度大于比较电平时，会将干扰信号误判为高电平;当磁铁与检测线圈位置过近，回波信号进入到激励信号震荡区域时，激励信号与回波信号在幅度上叠加，难以区分，存在测量盲区;回波信号的峰值点与方波信号上升沿通常不重合，也会导致一定的误差。

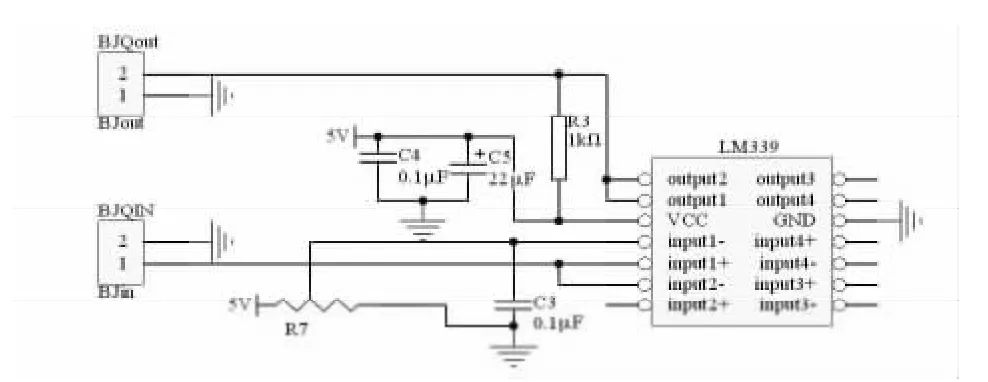
图2 硬件比较器电路图Fig 2 Circuit diagram of hardware comparator

3 基于DSP 的磁致伸缩位移测量

3.1 信号采样与滤波

实验中，磁致伸缩位移传感器电路单元所产生周期电流脉冲的幅度24 V，脉宽28 μs，频率为1.22 kHz。基于DSP的信号处理流程图如图3 所示。

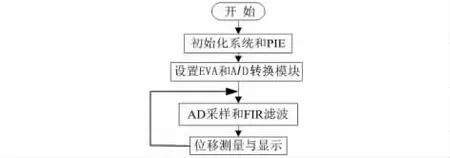
图3 基于DSP 的信号处理流程图Fig 3 Flowchart of DSP-based signal processing

TMS320F2812 芯片采集接收线圈接收的信号包含了激励信号、回波信号以及噪声信号。A/D 转换器和事件管理器EVA 是TMS320F2812 的外围设备，对信号采样。锁相环寄存器提供系统时钟，高速外设时钟预定标寄存器为A/D 转换器和EVA 提供高速外设时钟。EVA 的周期寄存器T1PR 决定了通用定时器GP1 计数周期，设置GP1 的下溢中断事件启动A/D 转换器，从而准确控制采样频率。A/D采样的流程图如图4 所示。

图4 A/D 采样原理图Fig 4 Principle diagram of A/D sampling

波导管的电流脉冲和激励脉冲会对信号产生一定程度的干扰，剩磁现象也会降低系统的信噪比，测量精度和量程将会受到影响。MAX275 是通用有源滤波器，通过将MAX275 的两个独立二阶滤波器级联实现四阶带通滤波器，能有效抑制回波信号中的噪声，也在一定程度上减弱了剩磁现象的干扰［10］。本文采用软件滤波的方法进一步改善信号质量。通过对采样信号进行FFT 分析，信号频率主要集中在60 kHz 以下，因此，设计了截止频率为65 kHz 的低通滤波器。

3.2 位移测量

激励信号峰值点为N1，回波信号峰值点为N2，激励信号和回波信号之间的间隔点数N=N2－N1，如果采样周期为T，则磁致伸缩位移传感器激励信号与回波信号的时间差t=NT，位移L 表示为

3.2.1 温度补偿设计

由于波导管材料本身的热弹性系数，波导管剪切弹性模量G 随着温度的升高而减小，从而导致扭转波传播速度v 改变，若不针对温度进行补偿设计，会使传感器位移测量值产生较大的误差，因此，实际测量中要对结果实时修正。Fe－Ga 合金中扭转波速与温度的关系如图5 所示。

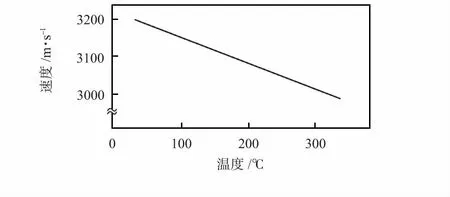
图5 Fe-Ga 合金扭转波速与温度的关系曲线Fig 5 Relationship curve of velocity of elastic wave and temperature of Fe-Ga alloys

实验中，利用两个位置磁铁实现温度补偿，基于硬件比较器的双磁铁温度补偿方法如图6 所示。在传感器前端某一固定位置处安放磁铁，精确位置为L1，产生回波信号1，回波信号2 由实际测量位移处磁铁产生，位移为L2，回波信号与激励信号之间的时间差分别为T1和T2。同一温度下扭转波速相同，得到

图6 采用温度补偿的信号Fig 6 Signals with temperature compensation

磁致伸缩信号经过DSP 采样和滤波后，两个回波信号与激励信号之间的间隔点数分别为N1'和N2'，可以得到

3.2.2 基于DSP 的双磁铁峰值检测

基于DSP 的双磁铁峰值检测流程图如图7。

4 实验结果与分析

图7 基于DSP 的双磁铁峰值检测流程图Fig 7 Flowchart of peak detection with double-magnet based on DSP

实验中，GP1 的计数频率F=18.75 MHz，计数周期TD=14，采样频率f=F/(TD+1)=1.25 MHz，采样周期T=1/f=0.8 μs。

实验中，固定磁铁与实际测量磁铁的位移精确值L1和L2由毫米尺测量得到，同时用硬件比较器法与峰值比较法分别计算测量磁铁位移，实验结果如图8 和图9 所示，固定磁铁精确值为12.06 cm，图8 的实际值为34.88 cm，硬件比较器法的测量误差较大，平均为0.56 cm，峰值检测法测量中，N1'=50，N2'=145，L=L1(N2'/N1')=34.97 cm，测量值基本在实际值附近，平均误差为0.09 cm。

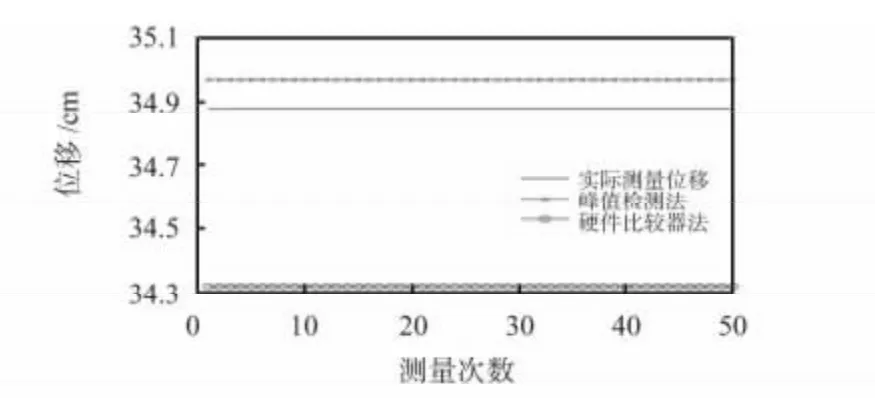
图8 位置1 的位移测量结果Fig 8 Displacement measurement results in position 1

图9 实际测量值为69.1 cm，硬件比较器法平均误差为1.38 cm，峰值检测法的平均误差为0.12 cm，实验结果证明:通过温度补偿设计，峰值检测法能够达到较高的测量精度。

图9 位置2 的位移测量结果Fig 9 Displacement measurement results in position 2

5 结束语

本文通过采用Fe83Ga17新型材料替代Fe－Ni 材料，改进磁致伸缩位移传感器，提高了传感器的测量量程，保证了稳定性。讨论了基于DSP(TMS320F2812)的磁致伸缩位移传感器信号处理的实现，利用DSP 实现磁致伸缩信号采样，设计了FIR 低通滤波器改善信号的质量。比较了硬件比较器法和峰值检测法的测量结果，并利用双磁铁实现温度补偿，从而获取精确可靠的数据。若要进一步提高分辨率，可以提高采样频率。

［1］ Hristoforou E.Magnetostrictive delay lines and their applications［J］.Sensors and Actuators A:Physical，1997，59:183－191.

［2］ Hiroyuki Wakiwaka，Muneo Mitamura.New magnetostrictive type torque sensor for steering shaft［J］.Sensors and Actuators A:Physical，2001，91:103－106.

［3］ 刘慧芳，贾振元，王福吉，等.超磁致伸缩力传感器及其实验研究［J］.仪表仪器学报，2011，51(6):3－5.

［4］ Zhou Xinzhi，Yu Chao，Tang Zhenyu，et al.Widemann effect in Fe83Ga17alloys for magnetostrictive sensors［J］.IEEE Sensors Journal，2014，14(1):249－257.

［5］ 余 超，周新志，熊胤琪.Fe83Ga17磁致伸缩位移传感器激励信号的ANSYS 分析及DSP 实现［J］.仪表技术与传感器，2012(8):4－6.

［6］ Yao Shixuan，Li Baoliang.A study on the precision improvement of the magnetostrictive linear position sensor［C］∥2010 Second International Workshop on Education Technology and Computer Science，2010:276－279.

［7］ Chang X M，Wakiwaka H，Ezawa M，et al.Accuracy enhancement on a long scale sensor using magnetostrictive wire by bipolar pulse current［C］∥The 2nd International Symposium on Linear Drives for Industry Applications，1998:151－154.

［8］ Clark A E，Teter J P，McMasters O D.Magnetostriction jumps in twinned Tb0.3Dy0.2Fe1.9［J］.Applied Physics A:Materials Science and Processing，1988，63(8):3910－3912.

［9］ Fernando Seco，Jose Miguel Martin，Jose Luis Pons，et al.Hysteresis compensation in a magnetostrictive linear position sensor［J］.Sensors and Actuators A:Physical，2004，110:247－253.

［10］冯希辰，周新志，余 超.磁致伸缩位移传感器回波信号滤波器设计［J］.传感器与微系统，2013，32(6):105－107.