基于RBF神经网络的燃气轮机转速传感器故障诊断研究
2015-03-25朱嵘嘉孟东曹丹丹
朱嵘嘉, 孟东, 曹丹丹
(第七O三所无锡分部,江苏 无锡 214151)
基于RBF神经网络的燃气轮机转速传感器故障诊断研究
朱嵘嘉, 孟东, 曹丹丹
(第七O三所无锡分部,江苏 无锡 214151)
提出基于径向基函数RBF(Radial Basis Function,简称RBF)神经网络的转速观测器,利用迭代增加神经元的方法解决了传统RBF网络神经元位置调整范围小和神经元数量固定带来的逼近不精确问题,并通过估计相对差和阀值的比较检测传感器故障。以某型燃气轮机转速试验数据为例进行了验证,证明RBF神经网络能准确进行转速传感器的故障检测,具有较好的工程应用价值。
RBF神经网络;燃气轮机;转速传感器;故障检测;估计相对差
0 引 言
燃气轮机低压、高压和动力涡轮转速为重要的检测参数,如传感器故障,产生错误监测信号会导致控制系统做出误动作,甚至引发重大事故[1]。然而,转速传感器工作环境复杂,存在水雾、盐雾、以及含钠、硫、钒等杂质的燃料燃烧所产生的腐蚀和老化[2-3]对燃气轮机动态特性的影响。因此,对转速传感器进行故障诊断就必须滤除上述干扰,即将传感器故障和燃气轮机本身特性变化引起的转速偏离区分开来。
故障诊断技术中的解析冗余法[4]克服了物理冗余法硬件结构复杂,实现成本高的缺点,但须建立较精确对象模型。近年来,神经网络被引入用于拟合对象模型。RBF神经网络的目标是在多维空间中寻找数据拟合的最佳平面,与传统BP网络相比,具有收敛速度快,函数逼近能力强的优点。但由于RBF网络的非线性映射能力体现在隐层基函数上,而基函数的特性主要由其中心位置确定,所以该方法比较依赖于神经元初始位置的选取,如选择不当,会增加神经网络的训练时间,易出现数据病态现象。
本文提出一种新型径向基神经网络,该网络在初始时定义神经元增加阀值α和神经元调整阀值β(α≫β),训练时,若逼近误差‖L(k)‖>α,则引入迭代增加神经元的方法训练网络,若β<‖L(k)‖≤α,则采用通常的神经元调整方法。与传统的RBF网络相比,该方法解决了神经元位置调整范围小和神经元数量固定带来逼近不精确的问题,其收敛速度更具优势,且只需定义神经元上限,就能避免随着神经元数目的增加带来的“维数爆炸”问题。本文将该RBF神经网络用于燃气轮机转速传感器的故障检测,利用神经网络重构燃气轮机转速输出,与实际传感器采样值比较,通过残差与阀值的比较实现故障诊断。
1 神经网络观测器设计
利用RBF神经网络可逼近任意连续有界非线性函数的能力,建立燃气轮机的非线性系统模型,进行故障诊断。考虑如下燃气轮机非线性控制系统:
xk=f(xk-1,uk-1),yk=g(xk,uk)+dk
(1)
其中u为系统输入,x为系统状态量,dk为系统不确定项(包括未建模动态,燃机特性参数变化及系统噪声等),f(·)和g(·)为非线性函数。显然,在非故障状态下存在实常数δ使得未知干扰输入dk满足:
‖dk‖≤δ‖xk‖
(2)
根据燃气轮机原理可知,燃气轮机工况变化对应其参数变化,即在外界环境一定的情况下(大气温度、压力不变),燃油流量可基本表征燃机的稳态工况变化,也就是说燃油流量与燃气轮机转速有较强的映射关系。即下式成立:
xk-1=g-1(yk-1,uk-1)
(3)
将(3)式代入(1)式可得如下输出方程:
yk=φ(yk-1,uk-1,uk)+dk
(4)
由(4)式建立神经网络转速观测器,整个故障诊断系统结构如图1所示。考虑到系统不确定项dk是有界的,且直接作用于系统输出yk,可将其看作系统本身的非线性特性。

图1 燃气轮机故障诊断系统结构图
设计无扰动神经网络转速观测器如下:
(5)
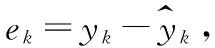
(6)
则利用故障阀值ε0的定义可实现故障检测,即:
(7)
2 神经网络观测器实现
2.1 神经网络结构
给定RBF神经网络的隐层初始神经元数为3,神经元上限为φ,同时按照给定规则自适应增加神经元,并在神经元增加至上限时自动删除对输入量影响最小的神经元,避免出现维数的过度扩张。以下给出神经网络输出函数:
(8)
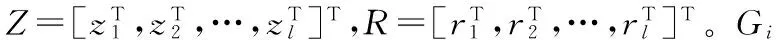
Gi=exp[-(‖X-zi‖/ri)2]
(9)
其中zi表示高斯函数中心向量。ri表示隐层神经元宽度。定义RBF神经网络逼近误差:
(10)
2.2 神经网络训练
已经证明,RBF神经网络在紧集合A上可以任意精度逼近任何非线性连续函数[5]。首先,根据已有的样本决定神经网络中心向量zi和神经元宽度ri的初值,同时保证隐层至少有一神经元中心向量非零,并给定神经元增加阀值α和神经元调整阀值(网络期望精度)β。随后进行在线训练,实时调整隐层权重向量wij,RBF神经网络在线训练算法如下:
(1)输入样本,计算各个隐层神经元输出Gi(Xi)和神经网络输出Uk(Xi)。
(2)由下式计算输入值到各个神经元中心距离ri:
(11)
(3)由(12)式计算网络逼近误差L(k),若L(k)>α且l<φ,则表示现有神经元数无法满足需要,则增加第R个输入向量为新神经元:
(12)
(4)若L(k)>α且满足条件l=φ,表示当前已经达到神经元数量上限,则需删除神经元Q:
(13)
(5)若α≥L(k)≥β,表示跟踪误差已减小至给定范围,采用隐层神经元调整算法,通过最小二乘法对中心点进行调整:
(14)
其中α(k)为神经网络学习速率,定义为神经网络逼近误差L(k)的线性函数,表示为:
α(k)=λ*L(k)
λ为给定正实数。
(6)在α≥L(k)≥β情况下,同时对网络隐层权重向量Wi进行调整:
(15)
(7)若满足L(k)<β,则停止训练;若不满足,转(1)步,重新进行计算。
2.3 神经网络神经元上限的确定
由于RBF是局部逼近神经网络,其在空间样本的输入局部区域内只有少量的连接权需要进行调整。在网络在初始训练阶段,通常情况下,其逼近误差‖L(k)‖远大于神经元增加阀值α,由此需通过增加神经元快速逼近给定目标。
在RBF神经网络设计中,所取神经元上限φ的值越大,则网络收敛性能越好,其拟合的曲线越平滑,但相应的,系统的计算量会同时大大增加,收敛时间也就越长。如φ值取得较小,网络的收敛误差则会增大。所以,在神经元上限φ值的选择上,要根据其拟合对象的收敛时间和收敛误差和合理折中选取。本文将某型船用燃气轮机运行试验数据引入神经网络进行训练,不同φ值下RBF神经网络的收敛时间和收敛误差见表1。
从表1中可以得出,选取的神经元上限不同,其网络收敛误差和收敛时间也不同。对于本文所选用的燃气轮机试验参数样本,在φ值为6或7时其收敛误差和收敛时间相对较小,而当选取的神经元上限大于9时,训练时间迅速增加,但收敛误差并未显著减小,这表明该值增加到一定数值后,对网络训练精度的影响就会迅速减弱。
2.4 故障判断阀值的确定与网络的更新
2.4.1 故障阀值的确定
由(7)式可知,为实现RBF神经网络的状态监测和故障判断,需选取合适的阀值ε0。对某型船用燃气轮机试验数据的整理分类,将燃油流量和高压涡轮转速输入构造的RBF神经网络,得到燃机转速的估计值。训练后,RBF神经网络观测器估计值与燃气轮机正常工况下的转速估计相对差曲线如图2所示。

表1 RBF神经网络收敛时间和收敛误差对照表
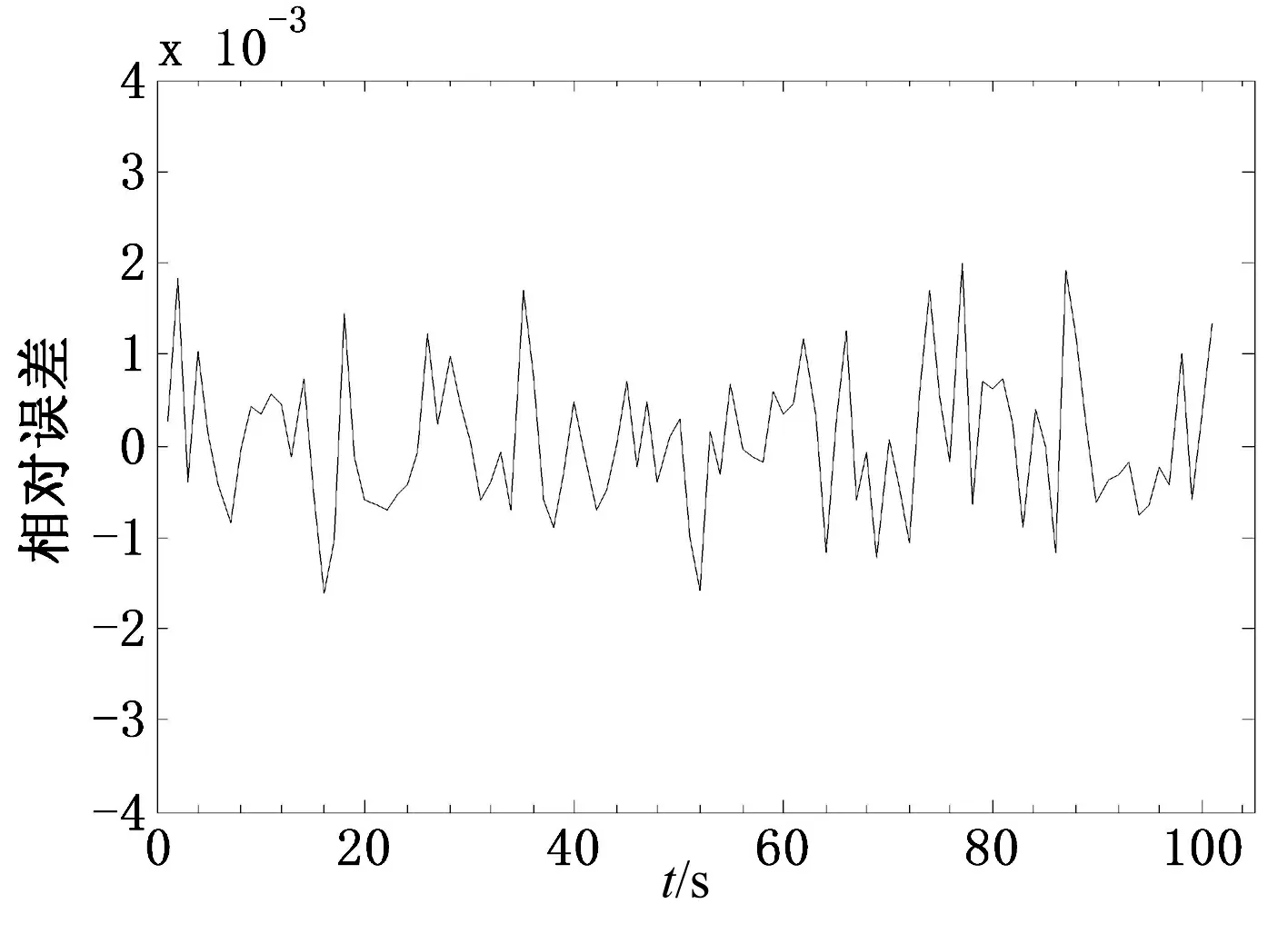
图2 正常工况下估计相对差曲线
如图2所示,在燃气轮机正常工况下,训练后的RBF神经网络和实际转速的相对差很小,最大相对差不超过0.002 5,因此,可将故障判断阀值取为0.003。
2.4.2 网络的更新
考虑到燃气轮机长久运行所产生的部件磨损和老化,如涡轮叶片的结垢、传感器安装间隙变化和油蚀等,会导致的转速和燃油量的对应关系产生变化。因此,需定期对神经网络训练样本进行更新,使其符合当前机组运行的实际状态。本文采用以温度差为判断依据的样本更新方式,取Tf为神经网络采样时的环境温度,Td为当前环境温度,有:
3 RBF神经网络转速观测器故障诊断

图3 传感器恒增益故障曲线

图4 恒增益故障估计相对差曲线
针对某型燃气轮机,采用RBF神经网络对高压涡轮转速样本进行训练。选取神经元上限为7,故障阀值为0.003。训练完成后,引入转速传感器故障发生前后6秒数据进行测试。图3为第6秒发生转速传感器恒增益故障。图5为在第6秒发生传感器短路故障。
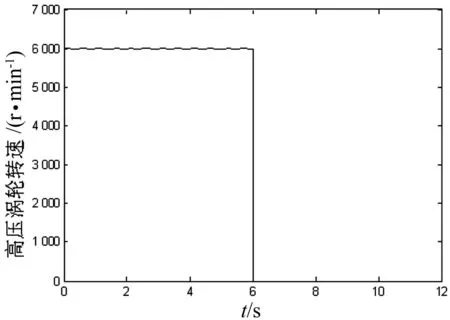
图5 传感器短路故障曲线
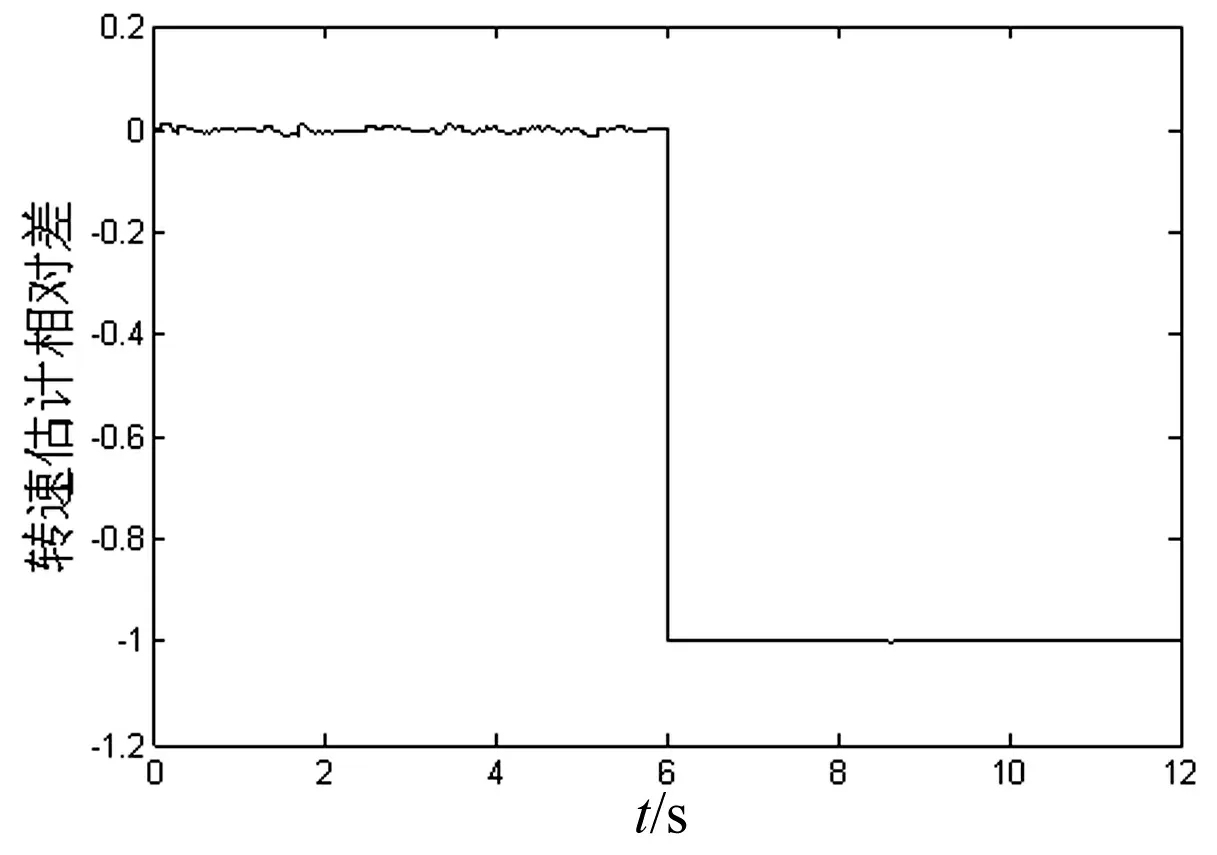
图6 短路故障估计相对差曲线
通过RBF神经网络估计相对差曲线(图4)可以看出,在传感器发生恒增益故障的时刻,估计相对差远远大于给定阀值,即使随着转速的增加,相对差略有下降,也不会影响神经网络的故障判断。由图6可以得出,发生短路故障时,神经网络估计相对差随即发生变化。
由上述试验结果可知,利用所设计的RBF神经网络观测器,在燃气轮机高压涡轮转速传感器故障情况下,能迅速利用转速采样值和观测器输出值计算估计相对差,实现故障诊断,其试验结果符合设计思想。
4 结束语
利用迭代增加神经元的方法建立了一种新型的RBF神经网络,解决了传统RBF网络神经元位置调整范围小和神经元数量固定带来的逼近不精确问题,针对燃气轮机转速传感器故障,采用该型RBF神经网络观测器实现转速的在线估计,通过转速估计相对差和故障阀值的比较,完成故障诊断。
[1] 薛银春, 孙建国. 燃气轮机控制技术综述[J]. 航空动力学报, 2005, 20(6):1065-1071.
[2] 朱嵘嘉, 吴一鸣, 尹菲. 基于分阶模糊自适应规则的燃气轮机控制研究[J]. 燃气轮机技术, 2013, 26(2):48-51.
[3] 陈娇, 王永泓, 翁史烈. 广义回归神经网络在燃气轮机排气温度传感器故障检测中的应用[J]. 中国电机工程学报, 2009, 29(32):92-97.[4] 谢彬, 李国宁, 冯涛,等. 神经网络在机车测速传感器故障诊断中的应用[J]. 机车电传动, 2012,53(6):84-87.
[5] 夏长亮, 祁温雅, 杨荣, 等. 基于RBF神经网络的超声波电机参数辨识与模型参考自适应控制[J]. 中国电机工程学报, 2004, 24(7), 117-121.
A Study on Speed Sensor Fault Diagnosis of the Gas Turbine Based on the RBF Neural Network
ZHU Rong-Jia, MENG Dong, CAO Dan-dan
(Wuxi Branch of No.703 Research Institute, Wuxi Jiangsu 214151, China)
This paper presents a speed observer based on the RBF (radial basis function) neural network, which uses the iteratively added nerve cell method to solve the problems of limited position adjustment range of nerve cells in the traditional RBF network and inaccurate approach due to fixed number of nerve cells. Furthermore, sensor faults are detected by comparing the estimated relative difference with the threshold value. The RBF neural network is verified by taking the speed test data of a certain model of gas turbine as example and is proved to be able to detect speed sensor faults accurately and have a good engineering application value.
RBF neural network, gas turbine, speed sensor, fault detection, estimated relative difference
10.3969/j·issn.1000-3886.2015.02.009
TP212
A
1000-3886(2015)02-0027-03
朱嵘嘉,(1980-),男,湖南湘乡人,硕士,高级工程师,中船重工集团703研究所无锡分部,研究方向为燃气轮机控制和故障检测。 孟东,(1983-),男,江苏人,硕士,工程师,中船重工集团703研究所无锡分部,研究方向为燃气轮机控制。 曹丹丹,(1981-),女,江苏无锡人,本科,工程师,中船重工集团703研究所无锡分部,研究方向为燃气轮机控制。
定稿日期: 2014-06-08
