(2+1)维Davey-StewartsonⅡ方程的精确解

施业琼

（广西科技大学 理学院，广西 柳州545006）

0 引言

自然科学领域的很多问题的数学模型最终可归结为非线性演化方程（组）来描述.由于这类方程的解析解对于洞察这些问题的物理本质具有很重要的意义，因此寻求非线性演化方程的孤子解一直是物理学和数学工作者的重点课题.到目前为止，人们已经发现并发展了基于计算机代数的许多直接方法，如齐次平衡法、Exp-函数法、辅助方程法、tanh-函数法等［1-6］是求解非线性偏微分方程的一个有效方法.

在广泛的流体力学问题中Davey-Stewartson系统（简称为DS方程组）在浅水波理论中是一个非常重要的模型，其形式可写为［7-9］（1）

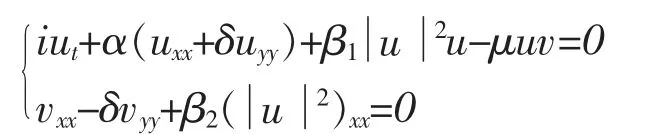
其中u为复函数，v为实函数，β1，β2为非线性系数，μ为相互作用系数，δ=±1，当δ=+1时，方程组（1）称为DSⅠ方程组；当δ=-1时，方程组（1）称为DSⅡ方程组.应用Darboux变换、散射反演法和Hirota方法［10-12］可以获得DS方程组（1）的多种孤立子解.本文在展开法［13-14］的基础上，对该方法进行推广，并运用于求解Davey-Stewartson方程的精确行波解的通解形式.

1 推广的-展开法的主要思想

考虑非线性偏微分方程：

式（2）就转化为只含行波变量ξ的常微分方程

2 应用推广的-展开法求解Davey-StewartsonⅡ（DSⅡ）方程

且ξ=αx+βy-2(pα-qβ)t，α，β，p，q，C1，C2为任意常数.

将解（19）～解（26）分别代入包络变换（8），即可得到（2+1）维Davey-Stewartson方程组（7）的精确包络波解，如：将式（19）代入式（8），可得到式（7）的精确解

其中,ξ=αx+βy-2(pα-qβ)t，θ=px+qy+[μ（α2-β2）+p2-q2]t.同理可得到其它类型的解，在此不再赘述.

若待定系数取解组（g）和（h）时，同样分λ2-4μ＜0,λ2-4μ=0,λ2-4μ＜0三种情形分别讨论方程组（9）的解，因方法类同故在这里就不详细讨论了.

3 结论

［1］Wang Mingliang.The Solitary Wave Solutions for Variant Boussinesq Equations［J］.Phys.Lett.A，1995，199：167-172.

［2］He J H，Wu X H.Exp-function Method for Nonlinear Wave Equations［J］.Chaos Solitons Fract，2006，30：700-708.

［3］施业琼.（2+1）维PKP方程的精确行波解［J］.钦州学院学报，2008，23（6）：18-20.

［4］施业琼，韩松.耦合修正Kadomtsev-Petviashvili方程的行波解［J］.广西工学院学报，2008，19（1）：9-12.

［5］刘式适，傅遵涛，刘式达，等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用［J］.物理学报，2001，50（11）：2068-2073.

［6］Fan Engui.Extended Tanh-function Method and its Application to Nonlinear Equations［J］.Phys.Lett.A，2000，277：212-218.

［7］Davey A，Stewartson K，Proc R，et al.On Three-dimensional Packets of Surface Waves［J］.Proc R Soc London Ser A，1974，338：101-110.

［8］Anker D，Freeman N C.On the Soliton Solutions of Davey-Stewartson Equation for Long Waves［J］.Proc R Soc London Ser A，1978，360：529-540.

［9］张金良，任东锋，王明亮，等.Davey-Stewartson 1的周期波解［J］.数学物理学报，2005，25A（2）：213-219.

［10］Ablowitz M J，Haberman R.Nonlinear Evolution Equationsin Twoand Three Dimensions［J］.Phys Rev Lett，1975，35（18）：1185-1188.

［11］Ghidaglia J M，Saut J C.On the Initial Value Problem for the Davey-Stewartson Systems［J］.Nonlinearity，1990，3（2）：475-506.

［12］Watanabe Y，TajiriM.Periodic Soliton Resonance：Solutions to the Davey-Stewartson I Equation［J］.J Phys Soc，1998，67（3）：705-708.

［13］Wang M L，Zhang J L，Li X Z.The（（G'）/（G））-expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics［J］.Phys Lett A，2008，372（4）：417-423.

［14］施业琼.高阶复系数Swift-Hohenberg方程的精确行波解［J］.广西工学院学报，2012，23（3）：15-19.