基于步进频连续波雷达的多目标识别方法

张 恒，姚森杰，董 曦

(1.中国船舶重工集团公司第723研究所，扬州 225001；2.镇江船艇学院，镇江 212000)



基于步进频连续波雷达的多目标识别方法

张 恒1，姚森杰2，董 曦1

(1.中国船舶重工集团公司第723研究所，扬州 225001；2.镇江船艇学院，镇江 212000)

步进频连续波雷达采用频率步进的连续波雷达发射波形，具有较高的距离分辨率。依据线性调频连续波雷达的二维快速傅里叶变换(FFT)算法和连续波频域测速理论，对步进频连续波雷达的目标识别方法进行了改进，实现了对多目标的识别，进行了仿真。结果表明该算法有效可行，具有较好的测距精度。

连续波雷达；步进频；多目标识别

0 引 言

连续波雷达虽然相较脉冲雷达发展较晚，但随着近年来对其理论研究的不断深入，其实际应用范围也在持续扩展。从民用领域的导航雷达到军用领域的战场监视，连续波体制雷达有着极大的发展潜力。其中单频连续波雷达主要用于多普勒测速，结构简单，但是不能得到目标的距离信息。调频连续波雷达可以探测目标的距离和速度，且不存在距离盲区，但是存在速度和距离耦合的问题。基于双频比相测距算法的多频连续波雷达，能够在测距的同时测速，也可以实现对多目标的识别，但是这种测距体制只能分离不同速度的目标[1]，对速度相同而距离不同的目标无法区分，应用存在较大的局限性。基于步进频连续波雷达理论，结合线性调频连续波雷达的二维FFT算法可以实现对多目标的识别[2]，还可以降低对数字信号处理机的瞬时带宽要求，而且系统结构和信号处理简单，容易实现杂波对消，所以近年来受到了广泛的关注。

1 步进频率连续波雷达原理

步进频连续波雷达[3]主要有锯齿型和三角型2种波形。这里以三角形步进频为例进行说明，其频率步进的信号波形如图1所示。

图1 三角型步进频率连续波雷达信号波形

由图1可知，某三角发射信号可由下式表达：

(1)

式中：f0为步进的基频；TR为每一次步进的持续时间；φi为每一次步进后波形的相位。

单目标时，在一个回波信号的频率递增部分[4]，回波信号经过混频和采样后得到每个步进频率信号的采样：

(2)

φ(i)=R0f0+i(ΔfR0-f0TRv)-i2vTRΔf

(3)

式中:At为幅度信息；R0为目标的起始距离；v为目标的运动速度。

式(3)中最后一项是耦合项，其大小相对于其他项可忽略，则：

φ(i)=R0f0+i(ΔfR0-f0TRv)

(4)

x(i)可看做单目标频域响应的采样，对采样得到的N个复数进行逆离散傅立叶变换，可知距离信息为：

(5)

由上式可知，在距离为R0时，目标在φ1时为峰值点，可得：

φ1=2N(ΔfR0-f0TRv)/c

(6)

同理，在回波的频率递减阶段，目标在φ2时为峰值点，可得：

φ2=2N(ΔfR0+f0TRv)/c

(7)

对运动目标，可求得其距离和速度。

目标距离为：

R0=[(φ1+φ2)/2]ΔR

(8)

目标速度为：

vr=[(φ2-φ1)/2]Δv

(9)

式中：ΔR=c/2B为距离分辨率;Δv=c/(2Nf0TR)为速度分辨率。

在存在多目标的情况下，可以使用频谱配对的方法来区分不同的目标。

2 步进频率连续波雷达对多目标的识别

前面介绍了步进频连续波雷达原理，传统的频谱配对算法较繁琐，实用性不强。利用线性调频连续波(LFMCW)雷达信号处理中的二维快速傅里叶变换(FFT)算法提出一种新的多目标识别方法。

以f0为基频，连续发射N个步进频率的连续波，每个连续波的发射时间均为T，步进频率为Δf，如图2、图3所示。

图2 步进频连续波雷达的发射波形

图3 系统框图

N组回波数据经过FFT处理后会得到N个通道的目标速度信息，然后对不同通道的同一速度单元的信号进行取模并积累，最后进行恒虚警率(CFAR)检测。设定合适的门限，检测值超过门限就说明该速度上存在目标。

假设在速度单元v上存在I个目标。取出N组FFT信号中对应的速度v单元上的共N个数据。设一个步进频连续波发射周期内依次发射的信号频率为f1，f2，…，fN。对频率为fn的回波信号的零中频采样数据进行M点FFT变换，则速度单元v上对应的信号为：

(10)

式中：T为每个步进频率连续波的持续时间；Al为第i个目标的回波幅度，且ωdn=2πfdnTs。

对Xn(kn)分别进行相位补偿和速度补偿，即将4πfnnvT/c和(ωdn-kn·2π/M)·(M-1)/2这2项补偿，只剩下初始距离影响的相位信息，可得：

(11)

然后对Y(n)进行离散傅里叶逆变换(IDFT)处理，即：

(12)

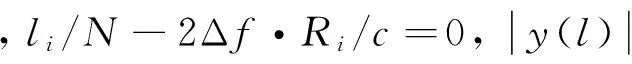
(13)

同理可知目标的距离分辨率为：

(14)

测距范围为：

(15)

3 仿真结果

由公式(14)和公式(15)可知，目标的最大测量距离Rmax和距离分辨力ΔR都与步进频率Δf有关；且随着Δf减小，最大测量距离增大，但是距离分辨力变差。因此可以在优先满足最大测量距离Rmax的前提下选择合适的步进频率Δf，然后适当增加步进频率个数N，这样可以保证对目标的距离分辨力要求。

仿真中取基频f0为2.5 GHz，每个步进频率信号的发射时间为20 μs，步进频率Δf为3kHz。为保证目标的距离分辨力，取步进频率的个数N为2 048，因此由公式(14)和公式(15)可得：最大测量距离Rmax为50km，目标的距离分辨率ΔR为24.41m。

第1次仿真，设有2个速度相同的运动目标，它们的距离分别为5km和15km，速度都为100m/s。步进频率连续波雷达收到2个目标的反射回波后，通过2 048个频率通道，经过相干检波后对每个频率通道上的信号进行采样，然后进行FFT运算。依次得到这2 048个频率通道上的频谱峰值，这样就知道了每个通道上的速度维的信息。将这2 048个峰值再进行一次1 024点的逆FFT(IFFT)运算，最后就得到了2个目标的距离信息。仿真的结果是：2个目标的距离分别是R1=4 984.68m，R2=14 980.91m；2个目标的测距误差分别是15.32m，19.09m。2个目标二维FFT算法的距离-幅度仿真图如图4所示。

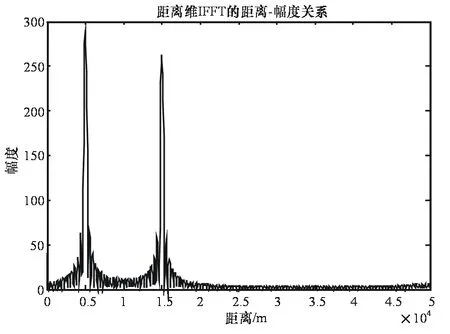
图4 2个目标二维FFT算法的距离-幅度仿真

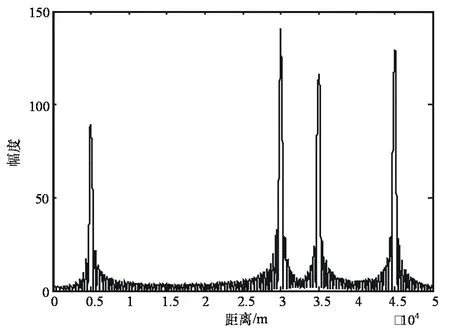
图5 4个目标二维FFT算法的距离-幅度仿真

第2次仿真，设有4个运动目标，它们的距离分别为5km，30km，35km和45km，速度分别为80m/s，100m/s，80m/s和100m/s。步进频率连续波雷达收到2个目标的反射回波后，通过2 048个频率通道，经过相干检波后对每个频率通道上的信号进行采样，然后进行FFT运算。每个频率通道会有2个速度信息，取出2个速度信息分别对应的2 048个峰值，再进行一次1 024点的IFFT运算，最后就得到了4个目标的距离信息。仿真的结果是:4个目标的距离分别是R1=4 980.45m，R2=299 986.29m，R3=34 988.67m，R4=44 991.04m。测距误差分别为19.55m，13.71m，11.33m，8.96m。2个目标二维FFT算法的距离-幅度仿真图如图5所示。

通过以上仿真可以看出，该算法需要较多的步进频率数N才能满足一定的测距精度，因此大量的FFT和IFFT运算使得计算量偏大。但是不论目标的速度是否相同，该步进频率连续波多目标算法都能够较好地识别多个运动目标，和频率配对法相比，该算法易于实现。

4 结束语

本文先给出了步进频连续波雷达的基本原理，然后基于LFMCW雷达信号处理中的二维FFT算法，给出了一种新的多目标识别方法。该算法需要对N个步进频率点回波先进行FFT运算，再对处理后数据的N个峰值进行IFFT处理，可以有效识别多个运动目标。该算法计算量较大，但是不需要频谱配对，且具有较好的测距精度，经仿真证明是有效的。

[1] 曹延伟,程翥,皇甫堪.基于二次相差法的多频连续波雷达测距算法研究[J].信号处理,2005,21(2)：178- 180.

[2] 王月鹏,赵国庆.二维FFT算法在LFMCW雷达信号处理中的应用及其性能分析[J].电子科技,2005(5)：25-28.

[3] 刘国伟,孙光民,顾红,等.连续波雷达及其信号处理技术[J].现代雷达.1995(6)：20-31.

[4] Li Zhaolong,Chen Rushan,Wu Ke.System design considerations of a generic integrated frequency modulation continuous wave radar Front-end[J].Microwave and Optical Technology Letters,2013,55(8):31-37.

Multi-target Recognition Method Based on Stepped-frequencyContinuous Wave Radar

ZHANG Heng1,YAO Sen-jie2,DONG Xi1

(1.The 723 Institute of CSIC,Yangzhou 225001,China；2.The Chinese People's Liberation Army in Zhenjiang Institute of Boats,Zhenjiang 212000,China)

The transmitting waveform of continuous-wave radar based on stepped frequency is used for stepped frequency continuous wave radar,which is provided with relatively high range resolution.Based on two-dimensional fast Fourier transform (FFT) algorithm and speed measuring theory in continuous wave frequency domain of linear frequency modulation continuous wave radar,this paper improves the target identification methods based on stepped frequency continuous wave radar,realizes the multi-target identification,performs the simulation.Results show that the algorithm is effective and feasible,and has superior range measuring accuracy.

continuous wave radar;stepped frequency;multi-target identification

2015-06-18

TN957.51

A

CN32-1413(2015)04-0066-04

10.16426/j.cnki.jcdzdk.2015.04.017