离散时间SM[K]/PH[K]/1/FCFS排队系统的年龄过程改进分析

高卓,徐德举

1.华南农业大学珠江学院,广东广州510900

2.首都师范大学数学科学学院,北京100048

离散时间SM[K]/PH[K]/1/FCFS排队系统的年龄过程改进分析

高卓1,徐德举2

1.华南农业大学珠江学院,广东广州510900

2.首都师范大学数学科学学院,北京100048

基于一个离散时间的排队系统：顾客有着多种类型，成批到达，到达过程是一个半马尔可夫过程，按照先来先服务的准则，并且每一个顾客的服务时间服从各自的PH分布。对这个离散时间SM[K]/PH[K]/1/FCFS排队系统年龄过程进行了详细分析，引进一些附加变量构造一个关于年龄过程的马尔可夫链，从而计算出年龄过程的转移矩阵。

排队系统;年龄过程;马尔可夫链;转移矩阵

现代通讯网络需要处理各类数据，这些数据在容量等方面是各不相同的。现代供应链的设计也是要满足顾客的不同需要，这相当于在排队系统中顾客是有类型的。在现实生活中我们还经常遇到成批到达的现象，例如在生产制造系统中，需要加工的部件成批到达加工车间；再如在库存系统中，顾客的需求按照复合泊松过程到达系统。以上这些现象都可以描述为成批到达的排队系统。由于这些随机系统的设计和功能分析的需要，我们将研究一类有着多种类型顾客的离散时间的排队模型，其顾客是批到达。

文献[1]介绍了离散时间SM[K]/PH[K]/1/FCFS排队系统，该系统有k个类型的顾客（其中k为正整数），所有的顾客都加入一个队列，遵守“先到先服务”的规则。顾客的到达过程是一个离散的半马尔可夫过程，每个顾客的服务时间服从离散的PH分布，他们相互独立且与其到达过程相互独立[1]。文献[4]主要讨论了离散时间状态下的批量到达排队系统，推广了经典的离散时间排队模型，考虑单个服务台的情形，假设顾客到达服从几何分布、每批到达的顾客数服从一般的离散分布、顾客的服务时间也服从几何分布，使用嵌入马尔可夫链的方法，分析得到了该随机排队系统的队长、等待队长、等待时间以及忙期等关键指标的母函数[4]。在文献[3]中到达过程是马尔可夫过程，这是与我们研究的排队系统最大的不同之处。我们考虑的是一个离散时间的更普遍的排队模型，构造广义的年龄过程，这个过程是没有水平0这个边界的。在一个服务台的情形下我们可以从这个年龄过程的平稳分布得到等待时间和逗留时间的分布。在文献[2]中引进一个由顾客批的年龄过程构造的GI/M/1型的马尔可夫链，于是，正在服务的顾客批的年龄、系统总的工作量、等待时间、不同批不同类型的顾客的逗留时间等这些变量的稳态分布也可以得到[2]。并且文献[2]证明出广义的年龄过程和广义的总的工作量过程有相同的稳态分布，等待时间和逗留时间的分布为PH分布，并得到这些PH分布的矩阵表示[2]。但分析过程有点差错，我们将在文献[2]的思想上进行改进，引进不同的附加变量。

1 广义的年龄过程的改进分析

在文献[2]中引进了一些附加变量构造了一个关于年龄过程ag(t)的马尔可夫链，但当ag(t)＜0时附加变量Ia(t)的定义与计算过程是不相符的，在此对这个过程进行改进，引进一些与到达位相和服务过程相关的附加变量。引进附加变量分情况讨论如下：

（1）ag(t)＜0时，我们引进三个附加变量Ia(t),J(t),Is(t)。我们由ag(t)＜0可得，此时系统为空，下一个顾客批还需要-ag(t)个时刻才能到达。我们用马尔可夫链{ξn,n≥0}来定义Ia(t)，Ia(t)=ξn，如果第n个顾客批为将要接受服务的顾客批，那么Ia(t)表示将要达到的顾客批到达系统时半马尔可夫链的状态，J(t),Is(t)则分别表示这个顾客批的类型和其初始服务位相。

（2）ag(t)≥0时，我们仍引进三个附加变量：Ia(t),J(t),Is(t)。因为这个时候系统中有顾客存在，那么Ia(t)=ξn，如果第n个顾客批为正在接受服务的顾客批，那么Ia(t)表示正在接受服务的那个顾客批到达系统时半马尔可夫链的状态，J(t),Is(t)则分别表示正在接受服务的那个顾客批的类型和在t时刻的服务位相。可以看到，在ag(t)＜0时系统为空，顾客批还需-ag(t)个时刻才能到达，那么其到达时半马尔可夫链的状态以及它的类型和初始服务位相应该是一个未知数。但是我们可以将这个时间提前，使Ia(t),J(t),Is(t)提前发生变化，这并不对顾客批到达系统后状态的转移构成影响。因此，我们这样构造是可行的，并且我们发现建立的这个过程{ag(t),Ia(t),J(t),Is(t),t≥0}在一个顾客批接受服务期间是具有马尔可夫性的：这是因为这个顾客批的服务时间是由一个潜在的马尔可夫链（PH分布）决定，Ia(t),J(t)在这期间是不发生变化的，而ag(t)的值增加1。在系统完成一个顾客批的服务时，根据马尔可夫链Ia(t)发生改变，并且决定了到达间隔，ag(t)的值也发生改变。J(t)也由马尔可夫链决定，Is(t)由服务时间的初始分布决定。因此，过程{ag(t),Ia(t),J(t),Is(t),t≥0}在一个顾客批服务完的时刻也是具有马尔可夫性的。综合以上，我们能看出我们建立的这个与ag(t)有关的过程是一个马尔可夫过程[5]。

经分析，构造的这个关于年龄过程的马尔可夫链{ag(t),Ia(t),J(t),Is(t),t≥0}的转移概率矩阵为：

2 关于年龄过程的转移概率矩阵的求解

（1）当ag(t)=x,x≤-1时，此时系统中为空，下一批顾客还要经过-x个时刻才能到达，在t+1时刻，顾客批要么还没有到达，要么刚到达系统开始接受服务，但至少能肯定这个顾客批没有服务完离开系统。那么应该有ag(t)随时间应该增加1，而Ia(t),Ia(t+1)都是指将要到达的这个顾客批到达系统时半马尔可夫链的状态，J(t),J(t+1)都是表示这个顾客批的类型，Is(t),Is(t+1)也都表示其初始服务位相。于是，当ag(t)=x,x≤-1时，于是，由状态按字典排序以及只有当y=x+1,j=j’,J=J’,i=i’时概率为1，则B=I(ma·mtot)×(ma·mtot)，而从ag(t)=x转到其他年龄的概率都为零。

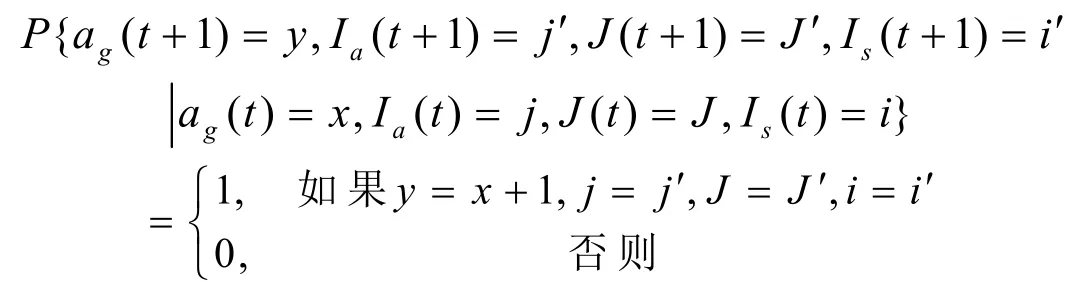
（2）当ag(t)=x,x≥0时，此时系统中至少有一个顾客批在接受服务，在t+1时刻，这个顾客批可能继续接受服务，也可能服务完毕离开系统。

如果t时刻接受服务的顾客批在t+1时刻继续接受服务，此时转移矩阵块为A0，那么应该有：ag(t+1)=x+1，而Ia(t)，Ia(t+1)都是指这个顾客批到达系统时半马尔可夫链的状态，J(t),J(t+1)都是表示这个顾客批的类型，但是Is(t)表示t时刻的服务位相，Is(t+1)表示t+1时刻的服务位相，这两者的变化由服务位相的转移矩阵决定。于是，

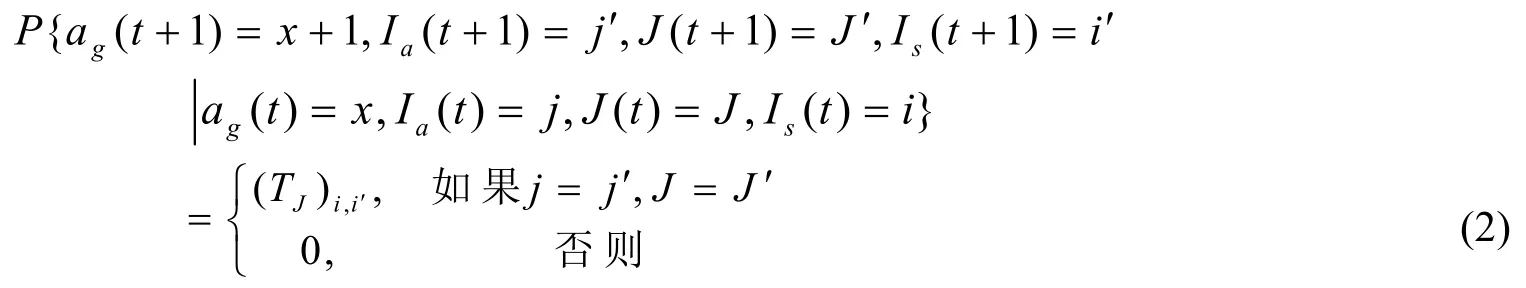
为了求出A0，我们根据状态按字典排序将A0这个(ma·mtot)×(ma·mtot)的矩阵块写成ma·ma个mtot·mtot的矩阵子块：

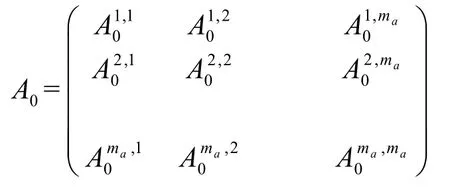
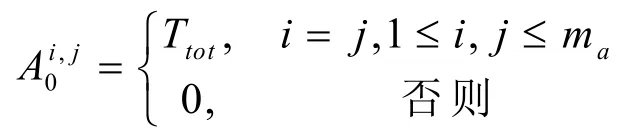
如果t时刻接受服务的顾客批在t+1时刻服务完毕离开系统，此时转移矩阵块为As,s≥1那么这时ag(t+1)与下一个顾客批有关，应有ag(t+1)=ag(t)+1-τn(t+1)+1。而Ia(t+1)是指下一个顾客批到达系统时半马尔可夫链的状态，J(t+1),Is(t+1)表示其类型和初始服务位相，于是，

同样为了求出As，我们同样根据状态按字典排序将As这个(ma·mtot)×(ma·mtot)的矩阵块写成ma·ma个mtot·mtot的矩阵子块：

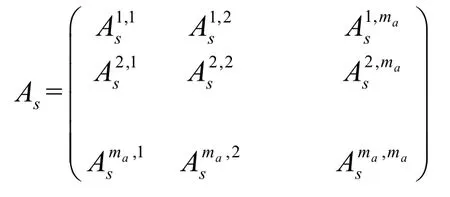
综合以上得到了转移矩阵Pg。

定理1SM[K]/PH[K]/1/FCFS的关于年龄的马尔可夫链的转移矩阵Pg为随机矩阵。

证明：

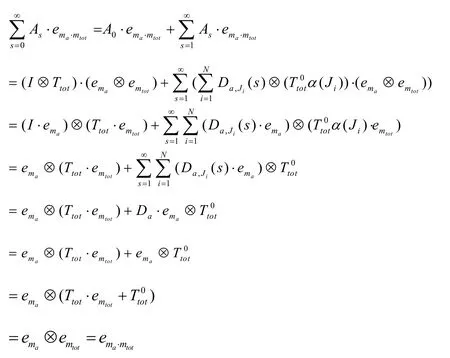
因此，转移矩阵是一个随机矩阵。

这与文献[2]中年龄过程的转移矩阵结果一样。我们也能从马尔科夫链{ag(t),Ia(t),J(t),Is(t),t≥0}得到很多关于年龄、系统闲期、逗留时间和等待时间的很多信息。并且，我们也可以和文献[2]一样从年龄过程的稳态分布得到它们的稳态分布。在这我们不再重复解决这个问题，有兴趣的读者可以参考文献[2]。

[1]高卓.离散时间SM[K]/PH[K]/1/FCFS排队系统的研究[J].科技信息,2014,5:7,32

[2]He Qi-ming.Age process,Workload Process,Sojourn Times,and Waiting Times in a Discrete Time SM[K]/PH[K]/1/FCFS Queue[J].Queuing Systems,2005,49(1):363-403

[3]Van Houdt B,Blondia C.The waiting time distribution of a type k customer in a discrete time MMAP[K]/PH[K]/c(c=1,2)queue using QBDs[J].Stochastic models,2004,20(1):55-69

[4]刘次华,何少锋.批量到达的离散时间排队系统[J].华中科技大学学报:自然科学版,2005,33(10):106-108

[5]Janssen AJEM,Van Leeuwaarden JSH.Analytic computation schemes for the discrete-time bulk service queue[J]. Queueing Systems,2005,50(2-3):141-163

[6]Marcel F Neuts.Matrix-geometric solutions in stochastic models[M].Baltimore and London:The Johns Hopkins University Press,1981

Analysis and Improvement of the Age Process in a Queuing System of Discrete TimeSM[K]/PH[K]/1/FCFS

GAO Zhuo1,XU De-ju2
1.Zhujiang College of South China Agricultural University,Guangzhou510900,China
2.School of Mathematical Sciences/Capital Normal University,Beijing100048,China

We studied a discrete time queuing system with multiple types of customers and a first-come-first-served(FCFS) service discipline.Customers arrive according to a semi-Markov arrival process and the service times of individual customers have PH-distributions.We studiedSM[K]/PH[K]/1/FCFSqueue and analyzed its generalized age process particularly.We introduced some auxiliary variables to construct a Markov chain associated withag(t)and obtained the transition probability matrix of this Markov chain.

Queuing systems;age process;Markov chain;the transition probability matrix

O226

:A

:1000-2324(2016)01-0923-04

2014-04-15

:2014-04-25

广东高校优秀青年创新人才培养计划项目(自然科学)(2013LYM_0117)

高卓(1981-),男,讲师,硕士研究生,主要研究方向:随机运筹学.E-mail:77275491@qq.com