基于测井数据小波变换和Hilbert-Huang变换的地层层序划分与对比

李雪梅,武爱华,乔田玲

1.泰安市水利和渔业局,山东泰安271000

2.泰安市岱岳区水务局,山东泰安271000

基于测井数据小波变换和Hilbert-Huang变换的地层层序划分与对比

李雪梅1,武爱华2,乔田玲2

1.泰安市水利和渔业局,山东泰安271000

2.泰安市岱岳区水务局,山东泰安271000

测井资料应用于地层层序研究的实例很多，一般选取能够敏感反映沉积堆积过程的GR或AC曲线作为研究基础，多注重测井曲线形态及幅值特征的应用。在前人所做工作的基础上，本文首先利用数学方法构建了测井仿真分段信号，然后利用一维连续小波变换和Hilbert-Huang变换对仿真信号进行了分析，验证了这两种方法的有效性及提出了两种分析方法的异同点。在此基础上，利用两种方法的结合对济阳坳陷惠民凹陷中钱斜14井沙河街组段的GR曲线进行了分析与层序划分，将其划分为三个三级层序。

小波变换;Hilbert-Huang变换;层序划分

层序地层划分的基本方法是以露头、岩心资料分析为基础，结合地震剖面、测井资料进行层序分析[1,2]。测井数据是目前连续性最好、分辨率最高的地质数据之一，并且随着科学技术的发展测井设备和测井结果也得到改善，这为层序地层学的研究提供了条件。测井资料应用于层序地层研究的实例很多，一般选取能够敏感反映沉积堆积过程的GR或AC曲线作为研究基础，多注重测井曲线形态及幅值特征的应用。测井数据所提供的有关地层的各种岩石物理参数对研究地层多级别旋回性具有独特的优势[3]。本文在前人所做工作的基础上，对小波变换和Hilbert-Huang变换在层序划分中的应用进行了总结对比。

1 小波变换

近年来，小波变换应用于测井层序地层研究备受关注，余继峰等首次探讨了测井数据小波变换的地质意义，2004、2005年发表了部分研究成果后[4-7]，受到较多关注，随后的类似研究日益增多，王志坤等、李霞、陈钢花等、房文静等、张莹等曾经应用测井数据小波变换进行了高分辨率层序地层研究[8-12]。

小波变换作为新的时频分析工具，具有良好的时频域分析特性。凭借小波变换的多分辨率特征和测井曲线的连续性，利用连续小波变换将测井信号从一维深度域转换为二维深度-尺度域，因此小波变换是用于沉积单元的界面分析、处理和解释测井资料、进行测井层序划分是可行的手段之一。

测井数据经过小波变换处理后，其中的频率结构得到清晰展现，据此可探测到各个频率段之间的突变点或突变区域，反映在地质问题上就是其形成环境的突变。测井数据经过一维连续小波变换后，可以得到一系列与尺度和深度对应的小波变换系数值。研究表明，由多个不同周期沉积旋回叠加的测井曲线，通过考察小波时频能量图局部能量团的变化和多种伸缩尺度的周期性震荡特征，可分析地层的旋回性并与各级层序界面建立对应关系，这就是小波时频分析划分地层的依据。

2 Hilbert-Huang变换

Hilbert-Huang变换是1998年由Norden E Huang等人提出的一信号分析方法。它是一种能够有效地分析线性/非线性，平稳/非平稳信号的时频分析方法。它的核心是经验模态分解（Empirical Mode Decomposition，简称EMD）和Hilbert谱分析（Hilbert Spectral Analysis，简称HAS）。在这个理论中，通过经验模态分解（EMD）将信号分解成有限多个内在模分量（Intrinsic Mode Function，简称IMF）和一个表征信号趋势变化的残余信号，并且提出对得到的各个IMF运用Hilbert变换进行时频分析。该方法通过提取复杂信号在每一个时刻局部的振荡模式，按由高到低的自适应频率分解模式寻找信号内蕴的高频信息。一般情况下，每个分解层的高频信息是具有时变频率特性的非线性高频信息。

测井信号的突变点代表地层信息变化，经验模态分解可以检测信号的突变点，利用该特性提取测井曲线的剧烈变化点，由此识别出地层不整合面和转换基准面，从而确定层序边界[13-15]。

应用多级分解下的IMF表现出的周期性振荡特征，将其与地质上划分的各级层序界面建立对应关系，不同频率的周期对应着不同规模的层序，各个频率段之间的突变点对应着层序界面，作为测井层序划分的依据，可以实现对地层层序划分。

3 层序地层划分

测井信号中蕴含了地层中的各种信息，包括大量的沉积学信息，其中包括岩石的化学成分、颗粒大小、胶结程度等等。层序的划分的关键是识别地层中不同的旋回周期，而旋回周期是通过这些沉积学信息反映出来的，测井信号的突变点反应了这些地层信息的变化，而层序的分界也往往是这些突变点所在之处。为了说明小波变换和Hilbert-Huang变换在层序划分中的异同点，本文借助于Matlab平台，利用数学运算构造并分析了理想测井信号模型，结合实例提出了两种方法的优缺点。

3.1 模型分析

系数的本文通过数学方法构造了一个分段的包含周期的仿真信号，构造过程如下：

函数sawtooth()是Matlab中产生锯齿波或三角波的函数，将产生周期为2π的锯齿波。sawtooth(t,width)中，width是0到1之间的标量。在0到2π×width区间内，x的值从-1线性变化到1；在2π×width～2π区间内，x的值又从1线性变化到-1。sawtooth(t,1)和sawtooth(t)是等价的。令x在0与12π之间均匀地取2400个数据，采样间距为π/200，然后将其按大小分为四段，分别按上述程序运算，所得结果如图1所示。

从构造过程可知，本文构造的分段仿真信号中包含有四个周期信号，而周期比为x之前的倒数比。分段信号中，第一段信号无偏移，在0点上下-5和5之间波动；第二段信号向上偏移5个单位，在0和10之间波动；第三段信号向下偏移5个单位，在-10和0之间波动；第四段信号无偏移，但将其振动幅度扩大4倍，在-20与20之间波动。分段信号之间没有过渡信号，均为突变，以此来模拟测井信号中的突变行为，即层序的分界点。

对构造的分段仿真信号进行Hilbert-Huang变换，得到七个IMF（图2）和Hilbert时频谱和边际谱（图3），由图3可以看出，仿真信号经过Hilbert-Huang变换后，其频率主要集中在0～0.1之间，但是基本分辨不出其中的频率变化。图2表明，部分IMF可以明确地指示出分段点处的位置。

图1 理想分段信号构造过程图Fig.1The construction process of ideal subsection signal

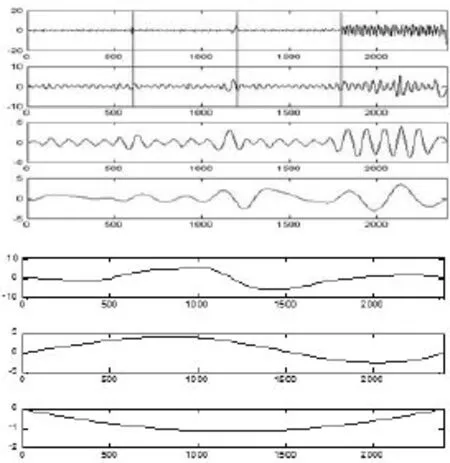
图2 分段仿真信号的EMD分解Fig.2 The EMD decomposition of segmented simulation signal

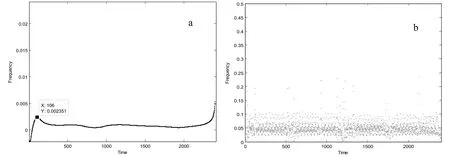
图3 Hilbert图谱a-边际谱；b-时频谱Fig.3 The Hilbert spectruma-marginal spectrum；b-time-frequency spectrum

对构造的分段仿真信号进行一维连续小波变换，可得到其小波能谱图（图4），由图4可以看出，仿真信号中分段位置处对应的小波能谱图中有明显的分界特点，并且信号中的周期性也可以在小波能谱图中得到体现。仿真信号中振动幅度大的部分在小波能谱图中表示很明显（能谱图中发亮的部位）。为了使得到的信息更加全面，本文利用一维连续小波变换模极值法选取了适当的小波系数曲线进行了分析[16]（图5、6）。

由图6和图7可以看出，小波变换也可以有效地识别出仿真信号中分段的位置点，但是，由于小波母函数的振动性，在分段点处小波系数曲线表现为一个小区间，而不是确切的一个点。而小波变换的优势在于它能识别信号中的周期性存在及信号中周期存在的稳定性。小波系数曲线中小波的振动幅度反映了该尺度对应周期存在的稳定性，即尺度16、33和84对应了其中的三个稳定周期，而且这三个尺度之比与分段信号中的周期之比1:2:5极为接近。另外，从模极值曲线上可以看到另外一个极大值点200，经放大观察，此点不能做到比相邻的两上以上点都大，所以不在考虑范围之内。

通过对分段仿真信号的分析可以看出，Hilbert-Huang变换与小波变换均可以识别信号中的突变点及变化趋势。Hilbert-Huang变换在突变点处的分辨率更高，对于突变点的识别更加准确，而小波变换测重于分析出信号中周期（旋回）的存在及表现情况，不同尺度的选择可以识别出信号中不同频率周期的存在，进而在实际测井信号中可以识别出不同级别的层序。

图4 小波变换的时频色谱图Fig.4 Wavelet transform time-frequency chromatogram

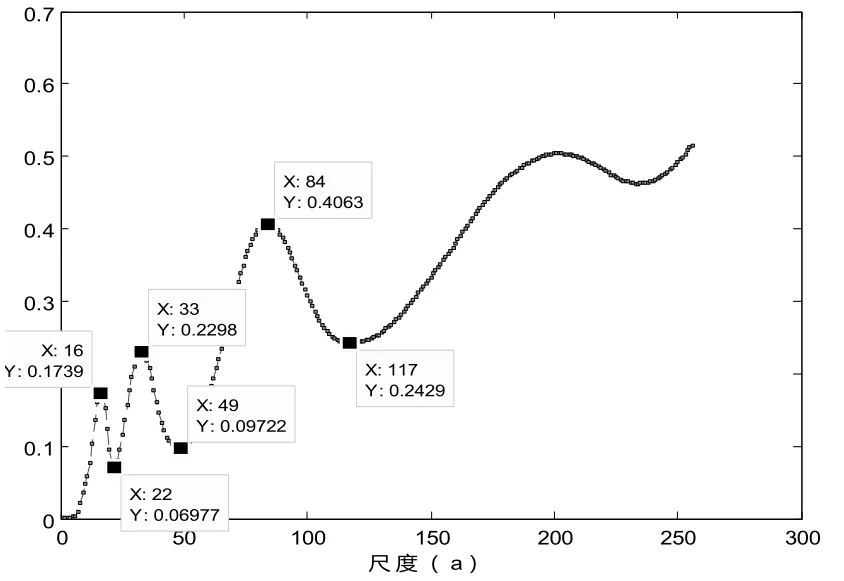
图5 小波系数模均值曲线Fig.5 Wavelet coefficients the mean modulus curve

图6 模极大值对应的小波系数曲线Fig.6 Modulus maximum of wavelet coefficient curve

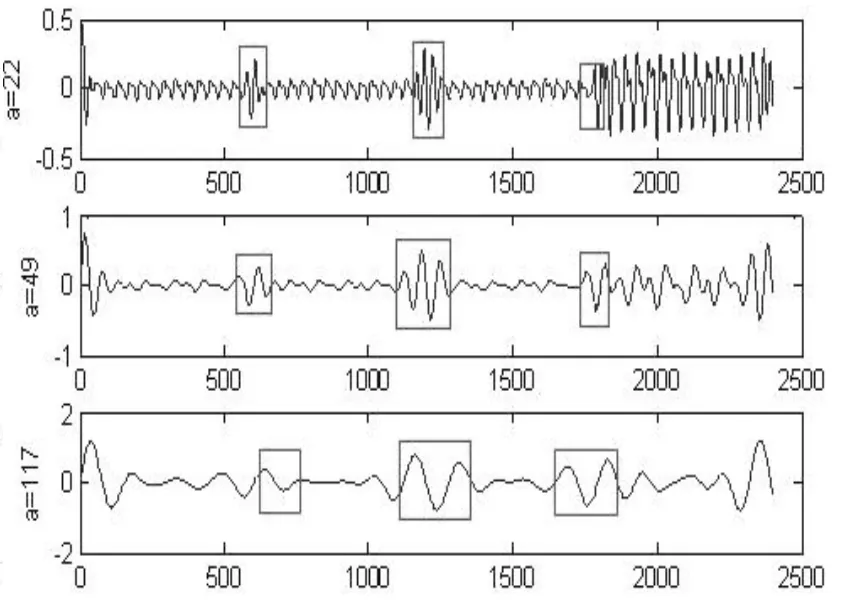
图7 模极小值对应的小波系数曲线Fig.7 Modulus minimum curve of wavelet coefficients

3.2 实例分析

本文选取了济阳坳陷惠民凹陷中的钱斜14井的沙河街组进行了分析，对钱斜14井沙河街组的自然伽玛曲线进行了Hilbert-Huang变换和一维连续小波变换，得到Hilbert-Huang变换后的11个IMF（图8），并选取了小波变换模极小值对应的3条小波系数曲线（图9、10），根据适当的IMF和3条小波系数曲线对钱斜14井的沙河街组进行了层序划分（图11）。从图11中可以看出，2400～2830 m为较细粒沉积物泥岩、粉砂岩为主，反映一个水深的沉积环境，为高水位体系域沉积；1830～2400 m发育完整层序——层序二，在约2100 m处以泥岩等细粒沉积物为主，为凝缩段沉积；1570～1830 m为较粗粒沉积物沉积，反映水进过程，为低体系域沉积。

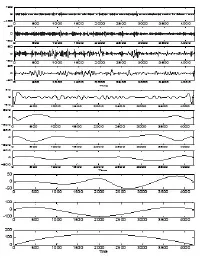
图8 自然伽玛测井信号的EMD分解Fig.8 Natural gamma logging signal EMD decomposition

图9 钱斜14井自然伽玛小波变换的时频色谱图Fig.9 Qianxie 14 wells natural gamma wavelet transform time-frequency chromatogram

图10 钱斜14井自然伽玛小波变换的模均值曲线Fig.10 Qianxie 14 wells natural gamma average wavelet transform modulus curve

图11 钱斜14井古近纪沙河街组层序划分Fig.11 Stratigraphic classification for 14 wells in paleogene of Shahejie Qianxie

根据Hilbert-Huang变换和小波变换的分析结果，本文将钱斜14井沙河街组分为三个三级层序，并识别出其中中长期旋回。由图11可以看出，在实际测井信号的分析，Hilbert-Huang变换侧重于分析信号中的突变点，而对于信号中存在的旋回及其稳定性分析能力较差；小波变换方法侧重于信号中旋回及其稳定性的分析，对于突变点处也有相应的表示，但相对于Hilbert-Huang变换其对于突变点的分析分辨率较低。

4 结论

（1）Hilbert-Huang变换与小波变换均可以识别信号中的突变点及变化趋势。Hilbert-Huang变换侧重于分析信号中的突变点，而对于信号中存在的旋回及其稳定性分析能力较差；小波变换方法侧重于信号中旋回及其稳定性的分析，对于突变点处也有相应的表示，但相对于Hilbert-Huang变换其对于突变点的分析分辨率较低。

（2）小波变换和Hilbert-Huang变换在层序划分中的应用各有利弊，在实际测井层序划分中应综合考虑多方因素、多种方法的结合，使层序划分结果更加可靠。

[1]朱筱敏.层序地层学原理及应用[M].北京:石油工业出版社,1998

[2]池秋鄂,龚福华.层序地层学基础与应用[M].北京:石油工业出版社,2001

[3]欧塞拉.测井资料地质解释[M].北京:石油工业出版社,1992

[4]余继峰,李增学.测井数据小波变换及其地质意义[J].中国矿业大学学报,2003,32(3):336-339

[5]李江涛,余继峰,李增学.基于测井数据小波变换的层序划分[J].煤田地质与勘探,2004,32(2):48-50

[6]余继峰,付文钊,袁学旭,等.测井沉积学研究进展[J].山东科技大学学报:自然科学版,2010,143(6):1-8

[7]余继峰,于泳,付文钊,等.测井数据Matlab插值与地质旋回性分析应用[J].煤炭学报,2011,36(10):1679-1682

[8]陈钢花,余杰,张孝珍.基于小波时频分析的测井层序地层划分方法[J].新疆石油地质,2007,28(3):355-358

[9]李霞,范宜仁,邓少贵.Morlet小波在测井层序地层划分中的应用[J].2006,29(6):402-406

[10]房文静.测井多尺度分析方法及应用研究[D].东营:中国石油大学,2007

[11]房文静,范宜仁,邓少贵,等.测井数据小波变换用于准层序研究[J].地层学杂志,2007,31(3):303-308

[12]王志坤,王多云,宋广寿,等.测井信号小波分析在高分辨率层序地层划分中的应用[J].大庆石油学院学报,2005,29(6):17-20

[14]文政,朱筱敏,金明玉,等.基于测井数据Hilbert-Huang变换的地层层序划分[J].测井技术,2007,31(6):533-536

[15]徐敬领,王贵文,刘洛夫,等.基于经验模态分解法的层序地层划分及对比研究[J].石油物探,2010,49(2):182-186

[16]Xu JL,Liu LF,Wang GW,et al.Geophysical methods for the study of sedimentary cycles[J].Petroleum Science,2009,6(3):259-265

[17]Yu JF,Fu WZ,Li Q,et al.Milankovitch cyclicity Feature Extraction from Magnetic Susceptibility Data of Strata[C]. Hong Kong:IEEE,2011:249-253

Stratigraphic Sequence Division and Correlation of Wavelet and Hilbert-Huang Transform Based on Well-logging Data

LI Xue-mei1,WU Ai-hua2,QIAO Tian-ling2
1.Tai'an Water and Fisheries Bureau,Taian271000,China
2.Tai'an Daiyue District Water Affairs Bureau,Tai'an271000,China

There are many examples to apply well-logging data to stratigraphic sequence.Generally GR or AC curve which can sensitively reflect the accumulation of deposition process is selected for a basic research and it is emphasized on the application of well-logging curve shape and amplitude characteristics.This paper first constructed the well-logging simulated segment signal using mathematical methods based on the previous works and then analyzed on the simulated signal with one-dimensional continuous wavelet and Hilbert-Huang transform to verify the effectiveness of the two methods and present the similarities and differences between them.On this basis,a combination of two methods was applied in 14 wells of the Shahe street segment of Huimin and Jiyang Qianxie to analyze GR curve and stratigraphic sequence to be divided into three sequences.

Wavelet transform;Hilbert-Huang transform;stratigraphic sequence division

TE122.24

:A

:1000-2324(2015)06-0887-05

2015-08-11

:2015-09-20

李雪梅(1965-),女,高级工程师,主要从事水资源管理工作.E-mail:424521148@qq.com