激光准直铬原子束三维仿真分析
2015-03-23张文涛熊显名
何 芬,张文涛,熊显名
(桂林电子科技大学电子工程与自动化学院,广西桂林541004)
1 引言
精确度非常好的纳米沉积条纹可以作为纳米计量传递标准用于原子力显微镜(AFM)和扫描式电子显微镜(SEM)等纳米测量工具的计量标准[1]。激光操纵中性原子是纳米材料制作的最主要技术手段,利用光子和原子之间的动量交换产生的共振辐射压力来使原子沉积在基板上形成纳米量级的沉积条纹。由于使用频率稳定的激光驻波场,在选定合适的原子后利用原子光刻技术能得到非常精确的平均间距在10-5量级上的沉积条纹。随着科技进步,人们发现一维纳米光栅在计量应用中有其局限性,只能在横向的一个维度内准直AFM及SEM等测量仪器。2012年,同济大学张萍萍等人用偏振方向平行于光场平面、正交激光驻波场形成的光格点的汇聚于沉积特性制作了二维纳米点[2]。实现纳米光栅和纳米点的原子光刻技术是有一定前提条件的,由于原子束的横向发散角和通量的大小会直接影响纳米沉积条纹或纳米沉积点的半峰全宽和对比度[3],因此原子束需要在较小的速度范围内高度平行地到达沉积所用的激光驻波场。这就需要对从原子炉中喷射出来的原子束进行多方位的有效准直,以减小原子束的发散角,降低原子运动速度并提高原子通量[4]。本文设计了一个由三组激光构成的激光准直场来准直原子束,应用蒙特卡罗方法,通过大量数据的统计实验模拟铬原子的运动轨迹并统计原子在荧光屏位置的落点分布,研究激光系统参数对准直效果的影响。
2 理论模型
自20世纪80年代激光制冷概念被提出以来,多普勒准直被认为是最早也是最简单的一种激光准直机制,它以二能级原子模型为基础利用半经典理论来探讨原子在激光准直场中的运动特性[5-6]。当原子沿着光的传播方向运动时,经过N次吸收光子并产生各向同性的自发辐射后,总动量变化量为所吸收光子的动量,原子就会受到与其运动方向相反的阻尼力的作用从而使其运动速度减小实现准直效果。两束同频率、同强度、同偏振方向、沿相反方向传输的光束构成的行波场作用于中性原子的耗散力可表示为[7]:
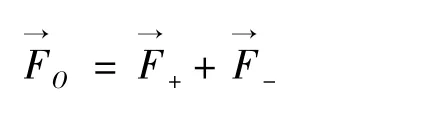

忽略(kv/Γ)4及更高次项,上式的一级近似可表示为[8]:

式中,h—为普朗克常量的1/2π;k为波矢;δ为激光频率与原子共振跃迁频率的矢谐量;S0为饱和参量;Γ为原子跃迁的自然线宽;β为阻尼系数。
由多普勒准直机制的原理可知,激光束只能减小沿着其方向运动的原子的横向速度。然而在制作纳米光栅,特别是制作二维纳米点的实验中,经过一个方向被准直的原子束已经无法满足实验的要求。为了更好地达到制作高精度的纳米光栅和纳米光点的实验要求,建立互相之间夹角为120°的三组激光构成的激光准直场。在理论模拟铬原子束三维准直过程中,定义原子束轴为z轴,原子束行进方向为z轴正方向,原子束横截面为xy平面,准直激光束模型如图1(a)所示。原子从高温的原子炉中喷出的速度是随机的,将其横向速度分解到x轴和y轴并分析在已经建立的三维光场中原子的受力情况如图1(b)所示。
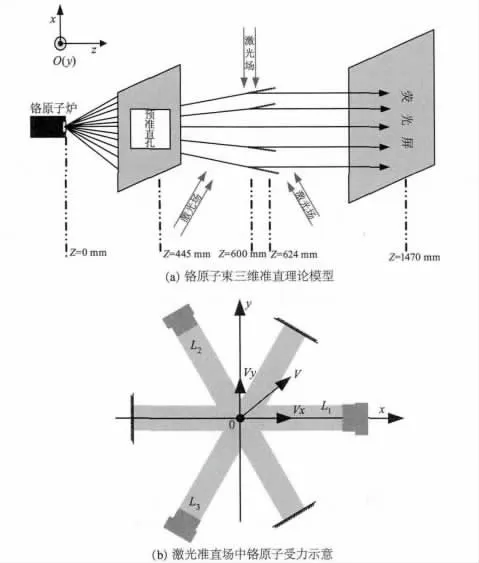
图1 铬原子三维准直原理及准直场中受力情况


原子在三维激光准直场中同时受到激光耗散力和重力的作用,其运动轨迹方程可表示为:

式中,G为原子所受的重力,由于原子在激光准直场中受到的耗散力远大于重力,且原子束的最可几速率远大于横向速度,因此在对原子束的横向准直进行定量的理论分析与模拟时忽略重力的作用。
3 基于蒙特卡罗方法的原子运动轨迹仿真
每个铬原子从原子炉中被喷出时的运动状态是随机的,可以用一组数 (xi,yi,Vi,αi,θi,ri)来表示第i个铬原子的初始运动状态,其中(xi,yi)表示原子从原子炉口被喷出时的初始位置,由于实验用坩埚出口直径为1 mm,则xi和yi均选择[-0.5 mm,0.5 mm]的均匀分布随机数。Vi表示原子的初始纵向速度,满足麦克斯韦-玻尔兹曼分布律。αi和θi分别表示原子初始发散角,定义为原子初始横向速度与纵向速度的比值,符合高斯分布。纵向速度 Vi与发散角 αi、θi均满足联合分布函数[9]:
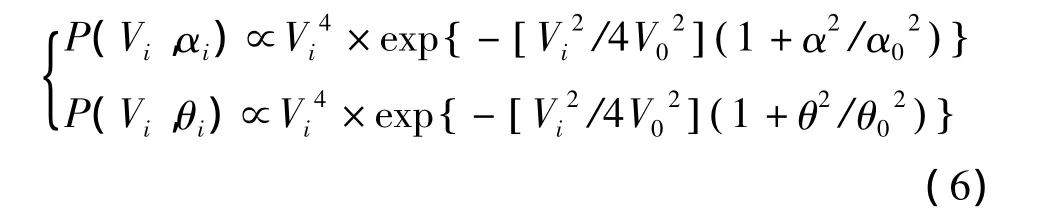
实验中,在真空条件下原子炉加热至1650℃时铬原子从炉口喷出形成稳定的铬原子源,其最可几速率约为960 m/s,原子的初始纵向速度Vi取麦克斯韦-玻尔兹曼分布。加入挡板后发散角αi和 θi最大值为 4.5 mrad,因此 αi和 θi均取[-4.5 mrad,4.5 mrad]的均匀分布随机数。Pαi和 Pθi取[0,1]内的均匀分布,然后比较 Pαi和 P(Vi,αi)的值以及 Pθi和 P(Vi,θi)的值,若 Pαi≤ P(Vi,αi)和Pθi≤ P(Vi,θi)同时满足则选取的 Vi、αi和 θi有效,反之无效,则重复上述过程直到选取的随机点满足条件为止。
在激光准直铬原子的实验中,只有52Cr原子能与给定的激光行波场产生相互作用力,其他同位素如50Cr、53Cr和54Cr等均不受到激光准直场的影响,ri表示该铬原子是否为52Cr原子的同位素。自然界中52Cr原子所占比重最大丰度达到了84%,剩下的同位素总和只占16%。因此,首先选取随机数ri服从[0,1]之间的均匀分布,ri∈[0.16,1]时认为产生的原子为52Cr,原子在激光准直场中的运动轨迹需要考虑耗散力;ri∈[0,0.16]时认为原子的属性为52Cr的同位素,原子在激光准直场中的运动轨迹不必考虑耗散力。
由此,我们通过蒙特卡罗思想确定了单个铬原子从原子炉喷出时的初始状态(xi,yi,Vi,αi,θi,ri),就可以根据原子的运动轨迹方程(6)来追踪原子运动轨迹并得出荧光屏处原子密度的分布情况,如图2所示。
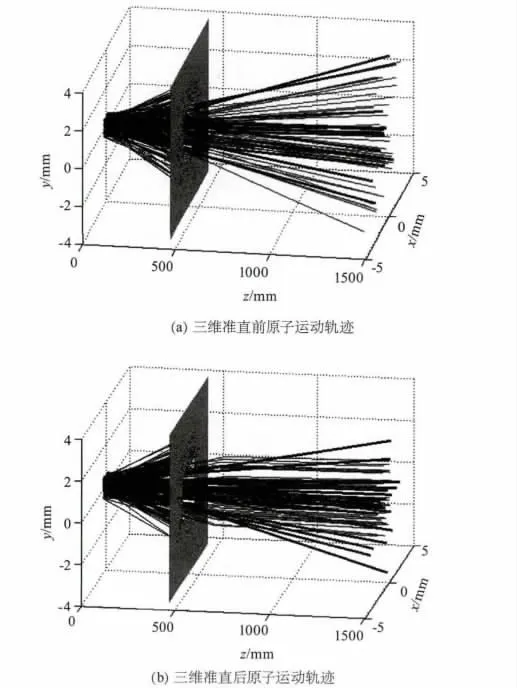
图2 铬原子运动轨迹
图2是蒙特卡罗方法模拟三维准直前后铬原子的运动轨迹,粗线部分表示除52Cr外其他铬原子的同位素。比较图2(a)和图2(b)可知经过三维激光准直场后部分铬原子的运动轨迹发生了明显的变化,这部分是52Cr原子在多普勒准直力的作用下原子的速率减小且温度降低使得原子束的发散角减小。由于铬原子的其他同位素在给定的激光准直场中与激光没有相互作用力,图2中粗线表示的原子运动轨迹在经过激光准直场后不发生改变。
4 铬原子经激光准直场后3维落点分布分析
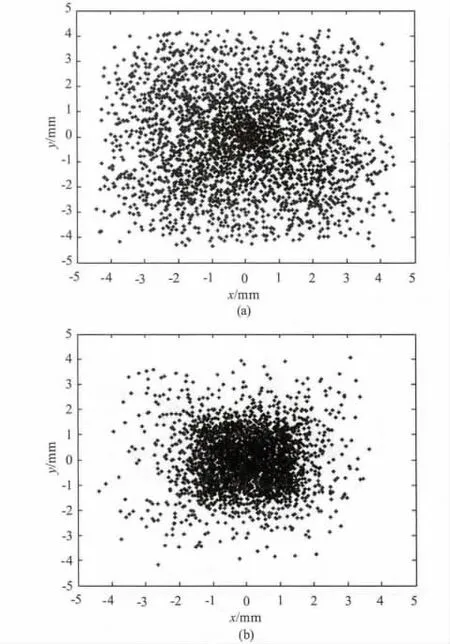
图3 铬原子落点二维分布示意图
图3是铬原子在荧光屏位置(即:z=1470 mm)的落点示意图,图3(a)是铬原子束不经过激光准直场直接落到荧光屏上的位置示意图,每一个黑点都表示一个铬原子的落点,图3(b)是铬原子束经过激光准直场后落到荧光屏上的位置示意图。对比图3(a)和图3(b)可知,尽管仍有部分原子的落点散落在离准直孔较远的位置,但铬原子束中的大部分原子经过激光准直场的准直后的落点比准直前的落点更向准直孔中心位置聚集。
相应的数值分析能更精确地显示激光准直的效果,本文对10000个原子进行了数值分析,对每个铬原子在激光准直场运动到达荧光屏所处的位置时的落点进行了数值统计分析。如表1和表2所示,x轴和y轴按照1 mm的间隔分割把荧光屏上的区域分为多个1 mm×1 mm的区域,表中的数字表示对落在各个区域的铬原子进行累计的个数总和。表1描述的是铬原子束未经过激光准直的原子落点个数统计;表2描述的是铬原子束经过激光准直后的原子落点个数统计。表中铬原子所处的横向位置与原子的横向速度成正比,铬原子横向速度越大,落在荧光屏上的横向位置就越偏离中心位置;铬原子横向速度越小,落在荧光屏上的横向位置就越靠近中心位置[10]。由表1和表2可知在荧光屏的中心位置即x和y均在[-0.5 mm 0.5 mm]区域时原子数目出现最大值。通过对比表1和表2中相同的位置的数值,原子数峰值由准直前的252在准直后达到503,且边缘区域的原子个数在经过激光准直后得到了很大程度的减小。说明原子束在经过激光准直后横向速度减小,经计算准直前铬原子束的最大发散角约为4.5 mrad,经过所设计的激光准直场后铬原子束的x方向最大发散角减小至1.5 mrad,y方向最大发散角减小至1.6 mrad。
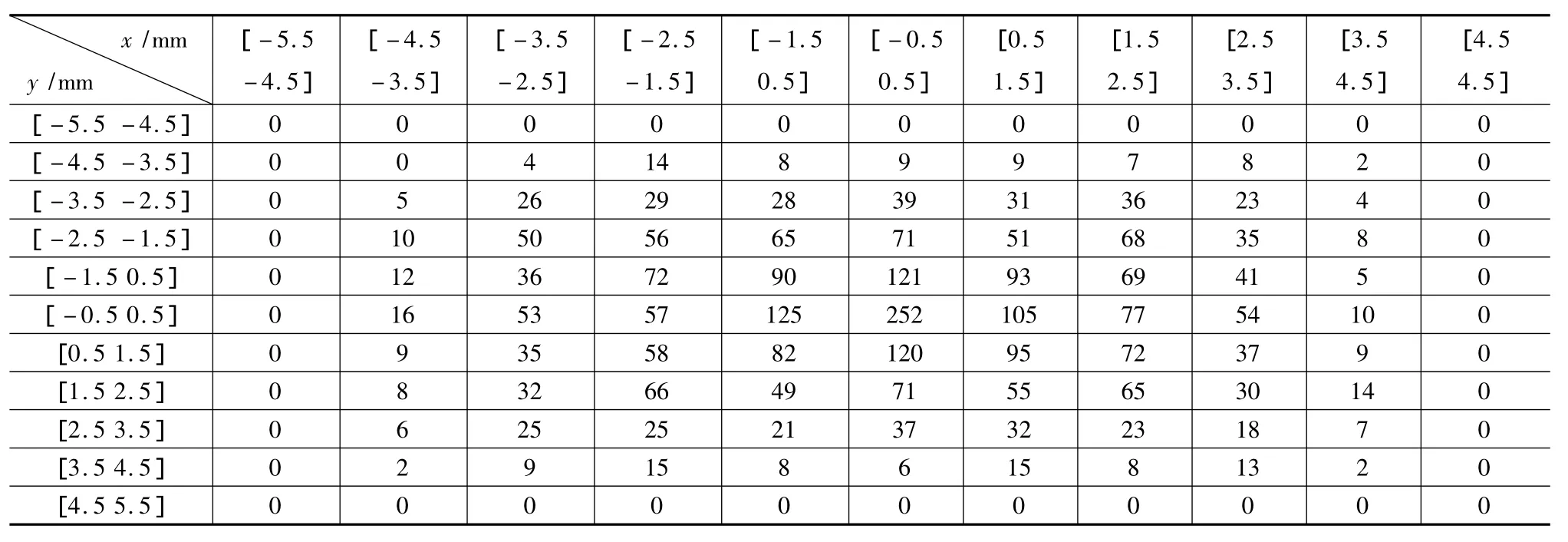
表1 激光准直前原子落点个数统计

表2 激光准直后原子落点个数统计
为了更直观地观察激光准直的三维效果,将原子的落点位置累积构成如图4所示的铬原子三维落点分布图。图4(a)和图4(b)分别是从同一个角度观察的铬原子未经激光准直场准直的三维落点分布和铬原子束经激光准直场准直后的三维落点分布。图4(a)和图4(b)的比较显示,经过激光准直场准直后原子累积的数目从边缘向中心增加的程度增大,说明文中设计的三维激光准直场对铬原子束的各个方向的准直效果均很明显。
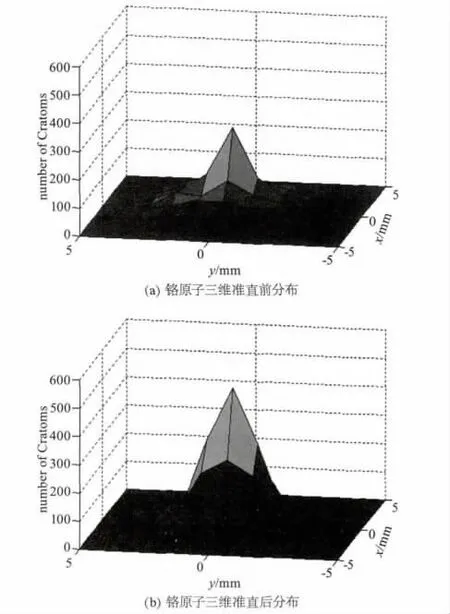
图4 铬原子落点三维分布图
5 结论
本文基于原子光学中多普勒准直原理,设计了一个由三组激光构成的激光准直场,应用蒙特卡罗方法模拟中性铬原子运动初始条件模拟中性铬原子在实际状况下在所设计的激光准直场中的运动轨迹,并对准直后原子的落点进行三维分析。对三维激光准直铬原子束过程的模拟证明,经过本文所设计的激光准直场的准直后铬原子的落点向中心方向聚拢,铬原子束的发散角在x方向和y方向分别减小至原来的33%和35%,为制作纳米光栅和纳米点提供了有利条件。本文所采用的蒙特卡罗方法在对铬原子在激光准直场受到多普勒力作用下的各项特性分析时充分考虑了52Cr以外其他同位素、铬原子初始发散角的随机性等因素对铬原子束横向激光准直的影响,使仿真在更加符合原子运动不确定性原理下进行,使结果更贴近实际情况为实际实验中的各项参数提供了有力依据。
[1] LI T B.Nanometrology and transfer standard[J].Shanghai Measurement and Testing,2005,1:8-13.(in Chinese)李同保.纳米计量与传递标准[J].上海计量测试,2005,1:8-13.
[2] ZHANG P P,MA Y,LI T B.Numerical simulation of 2D atom lithography via Monte Carlo method[J].Journal of Tongji University:Natural Science,2012,08:1270-1275.(in Chinese)张萍萍,马艳,李同保.蒙特卡罗方法数值模拟二维原子光刻[J].同济大学学报:自然科学版,2012,(8):1270-1275.
[3] MA Y,Zhang B W,Zheng C L,et al.Experimental study of laser collimation of Cr beam[J].Acta Physica Sinica,2006,55(8):4086-4090.(in Chinese)马艳,张宝武,郑春兰,等.激光准直Cr原子束的实验研究[J].物理学报,2006,55(8):4086-4090.
[4] ZHANG B W,ZHANG P P,MA Y,et al.Simulations of one-dimensional transverse laser cooling of Cr atomic beam with Monte Carlo method[J].Acta Physica Sinica,2011,60(11):113701.(in Chinese)张宝武,张萍萍,马艳,等.铬原子束横向一维激光冷却的蒙特卡罗方法仿真[J].物理学报,2011,60(11):113701.
[5] ZHANG W T,LI T B.Doppler laser cooling of chromium atom beam[J].Journal of Guilin University of Electronic Technology,2006,03:174-176.(in Chinese)张文涛,李同保.铬原子束的激光多普勒冷却[J].桂林电子工业学院学报,2006,03:174-176.
[6] ZHANG B W,Li T B,Ma Y.One-dimensional doppler laser collimation of chromium beam with a novel precollimating scheme[J].Chinese Optics Letters,2008,06(10):782-784.
[7] ZHANG W T,Li T B,Zhang B W.A laser-cooled chromium atom beam for nanolithography[J].Nuclear Instruments and Methods in Physics Research,2007,B256:719-722.
[8] Metcalf H J,Straten P.Laser cooling and trapping[M].New York:Spring-Verlag,1999.
[9] McClelland J J.Atom-optical properties of a standingwave light field[J].Journal of the Optical Society of A-merica B,1995,10(12):1761-1768.
[10] LI Yanqun,XIONG Xianming,ZHANG Wentao.3-D analysis of laser-cooling Cr atoms[J].Laser Technology,2012,06:788-792.(in Chinese)李艳群,熊显名,张文涛.激光冷却铬原子的3维仿真分析[J].激光技术,2012,06:788-792.
