超空泡航行体鲁棒H∞绝对稳定控制

韩云涛，强宝琛，孙尧，白涛

(哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

在水中，当液体局部压力下降到一定程度时，超空化现象就会出现。利用超空化现象可以极大地减小航行体受到的阻力，使得航行体速度的提高成为可能。HSSV几乎整体包裹于空泡中，只有头部的空化器和后面的尾舵与水接触，随之产生的强烈非线性滑行力以及空泡形态变化等都给HSSV的稳定控制和机动带来了极大的困难［1］。国内外学者对HSSV的数学模型进行了研究:Dzielski等提出了一个4状态2自由度模［2］，Kirschner等提出了一个12状态6自由度模型［3］，Kulkarni等建立了一个4状态3自由度模型［4］，并且均设计了相应的控制器以稳定系统。文献［2，5-9］在Dzielski等提出的模型基础上分别应用反馈线性化、圆判据和滑模控制等方法进行了稳定性分析和控制器设计。但是上述文献对系统存在噪声干扰的情况却未加讨论。以圆判据形式给出的绝对稳定理论是非线性系统稳定性分析和控制器综合的有力手段，且特别适合处理系统非线性环节满足扇形区域有界条件的情况。文献［5-8］运用圆判据理论设计了控制器，在分析滑行力非线性特性的基础上，将滑行力视作扇形区域有界不确定性进而设计了绝对稳定控制器。但是受限于圆判据本身所适用的模型形式，当系统存在噪声干扰时，基于圆判据设计的控制器所获得的系统鲁棒性较差。近年来，从时域角度研究绝对稳定理论吸引了越来越多的学者的兴趣。相较于频域圆判据，时域绝对稳定判据在处理包含噪声干扰等因素的系统时具有较强的鲁棒性。本文考虑系统噪声干扰，从绝对稳定理论的时域角度出发，提出了一种鲁棒H∞绝对稳定控制器综合方法。

1 HSSV数学模型及系统分析

1.1 数学模型

Dzielski研究了HSSV的一个基准控制问题［2］，被引用较多。本文在Dzielski提出的模型上继续进行研究。其数学模型如下:

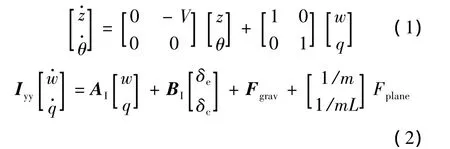
4个状态z、θ、w、q分别为航行体深度，俯仰角，纵向速度和俯仰角速度，δc和δe是控制输入，分别表示空化器转角和尾舵转角。同文献［5，7］，本文中滑行力表达式为

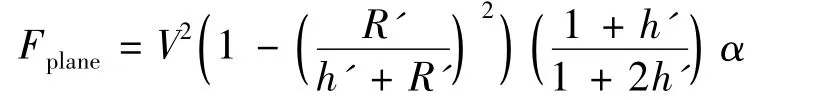
式中:R'=(Rc－R)/R，Rc为空泡半径，R为航行体半径。浸入深度h'和浸入角α分别表示为

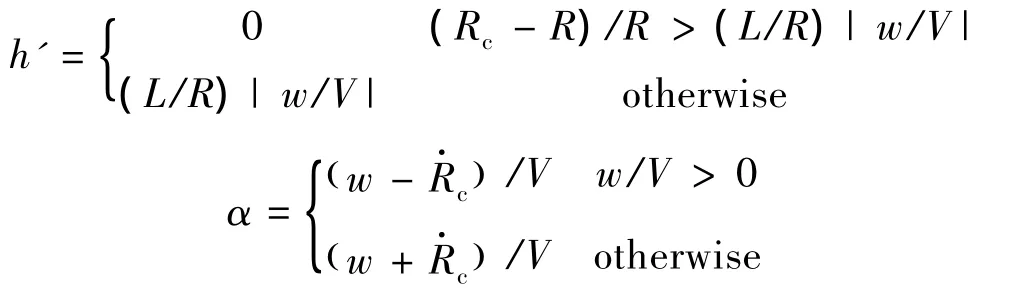
其余参数为Cz=1/2Cx，Cx=Cx0(1+σ)，其中σ表示空化数。R1=Rn/R，其中Rn为空化器半径。空泡半径收缩率为

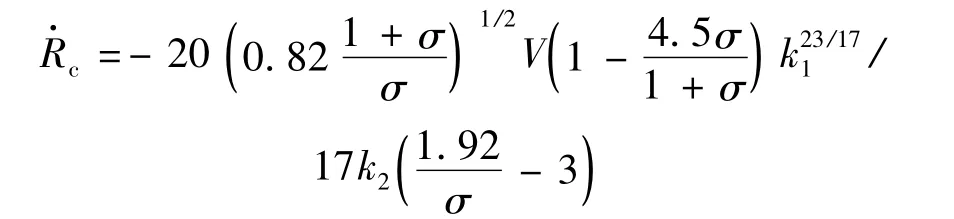
1.2 系统模型变换

分析系统模型可知，动力学方程(2)只与w，q有关，运动学方程包含3个状态变量z、θ和w，所以可将原系统(1)、(2)写成2个子系统级联的形式。为此，取η= [ z θ]T，ζ=[w q]T。令A2=，模型中其他矩阵定义如下:

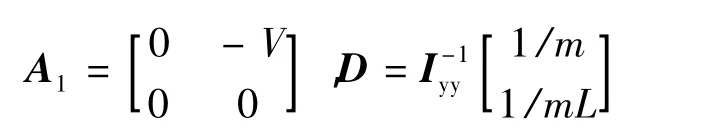
超空泡航行体在运动过程中，不可避免会受到洋流扰动、系统内部噪声等的影响。考虑噪声干扰时，式(1)、(2)有如下形式:

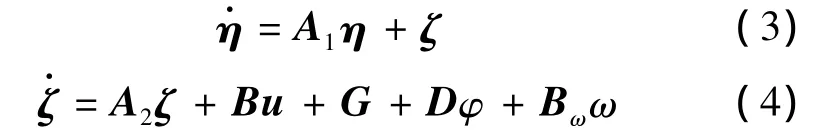
式中:Bω=I2为噪声驱动矩阵，ω∈R2×1是噪声向量且满足ω(t)∈L2(0，∞)。

由于本文的设计目标之一是航行体能够跟踪给定深度指令，为此将式(3)、(4)的镇定模型转化成跟踪模型。设zd、wd、θd、qd分别为给定的航行体深度指令、纵向速度指令、航行体俯仰角指令和俯仰角速度指令。令误差向量ηe=η－ηd，ζe=ζ－ζd，其中ηd= [zdθd]T、ζd= [wdqd]T，代入式(3) (4)中替换η和ζ，得到

为了得到形如系统(3)(4)的backstepping跟踪模型，式(5)中右侧同时加减K1ηe有:

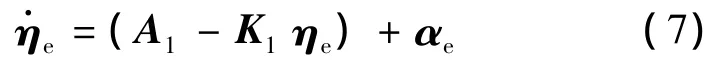
其中，

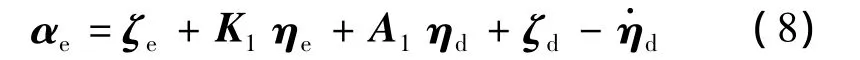
为新的状态变量。由此，新的跟踪模型应该是关于状态变量向量ηe和αe的方程，为了得到关于αe的状态方程，将式(8)对时间求导得)，将式(6)～(8)代入式(5)，整理得

其中，

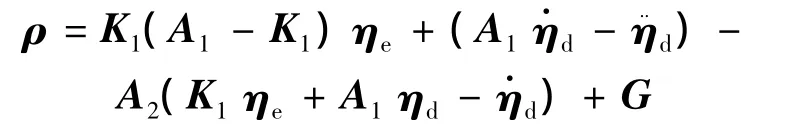
再考察输出向量，取C=[1 0]，y=w为唯一输出，则有y=Cζ=C(ζe+ζd)，将式(8)代入得

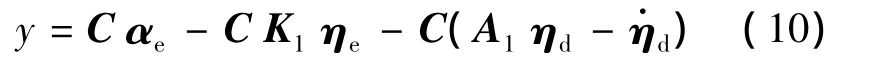
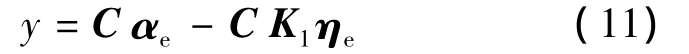
综上，得到了仅关于状态变量向量ηe和αe的跟踪模型如下:

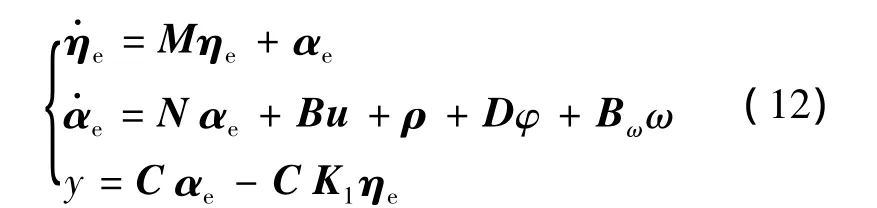
式中:M=A1－K1是Hurwitz的，N=K1+A2。

1.3 滑行力非线性特性分析

如文献［5-8］所述，滑行力是纵向速度w的函数，二者的关系如图1所示。

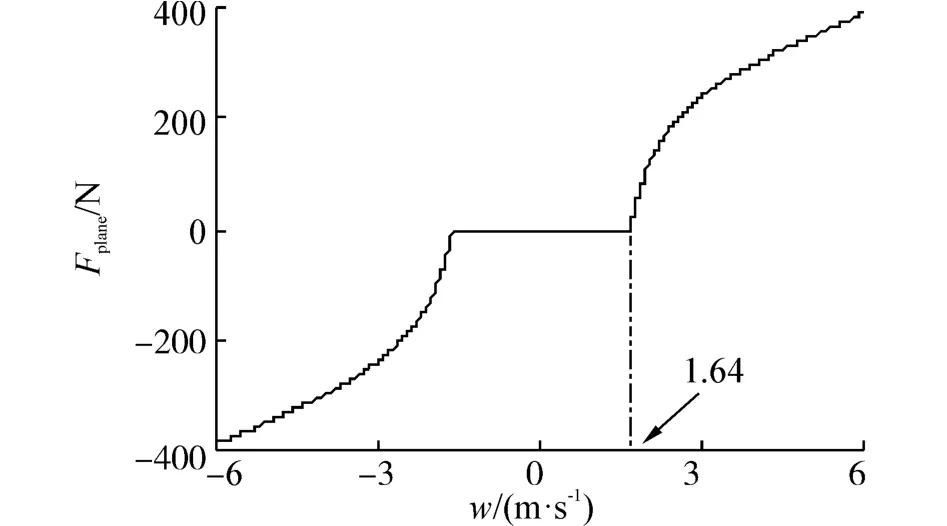
图1 滑行力与纵向速度的关系Fig.1 Relationship between vertical speed and planing force

由图1和绝对稳定性定义可知，滑行力的非线性特性整体处于扇形区域(Km是标量，表示曲线上的点与原点之间连线最大斜率)内，即有φT(φ－Kmw)=φT(φ－Kmy)≤0，将式(11)代入该式可得

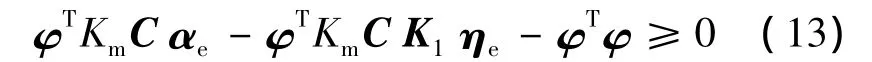
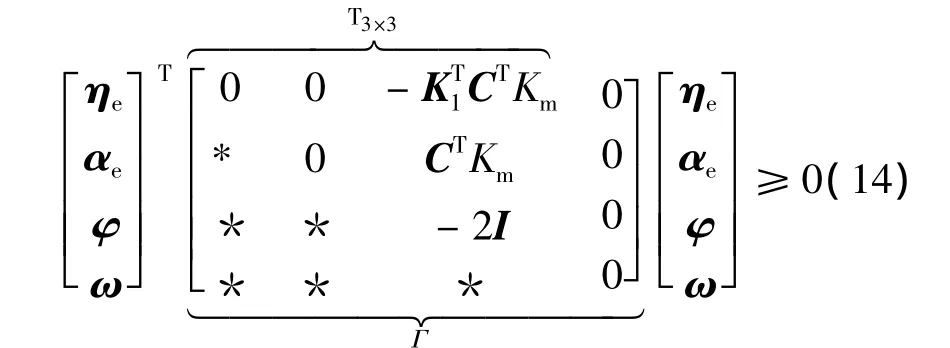
为满足下面定理的证明，将式(13)写成LMI的形式，即

2 控制器设计

由于系统中存在非线性滑行力，不能直接采用线性系统理论进行控制器设计。设计控制器时，可令u=B－1(ρ+N αe+Dφ+r)，得=r+Bωω。由此，非线性系统(12)转换为线性积分器反步的形式［10］，只需设计r使αe渐近稳定则有ηe渐近稳定。但是缺点在于，上述控制器引入了非线性滑行力φ，该力的模型具有很大的不确定性，并且通常情况下难以准确观测，这必然导致控制器的控制品质受到影响，严重时甚至导致控制发散。因此，设计状态反馈控制律如下:

本文的目标是设计状态反馈控制器(15)使得闭环系统(12)是内部稳定的，并且在零初始条件下具有给定的H∞扰动抑制水平γ。为此定义受控输出o和目标函数Joω分别为

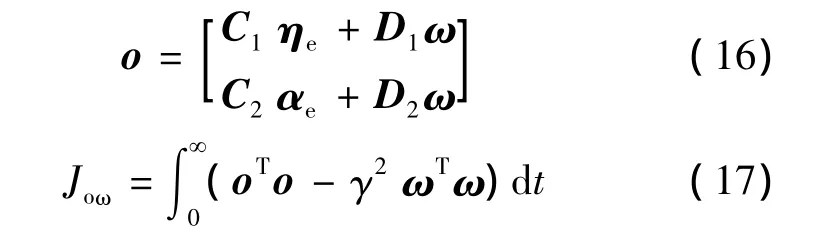
式中:C1=C2=D1=D2=I2。对于给定的标量γ＞0，把从噪声ω到受控输出o的传递函数Toω的H∞范数约束记做‖Toω‖ ＜γ，因为H∞范数在时域内等价于诱导2范数，所以采用如下表示方法:

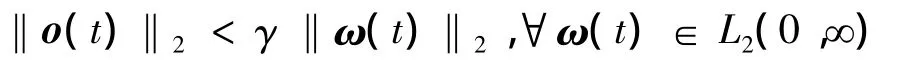
定义 考虑如下系统:

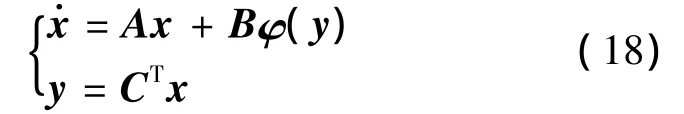
式中:x∈Rn为状态向量，A∈Rn×n，B∈Rn×m，C∈Rn×m为系统常数矩阵，φ(y)∈Rm×1是非线性函数，并且满足

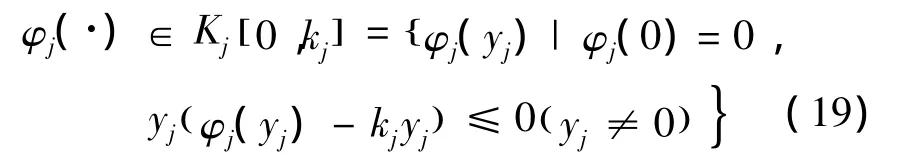
如果系统(18)对于所有满足式(19)的非线性特性φj(·)，j=1，2，…，m，原点都是全局一致渐近稳定的，则称系统(18)是绝对稳定的。其中，yj是向量y的第j个分量。

下面，将应用Lyapunov理论进行控制器设计。定义备选Lyapunov函数为

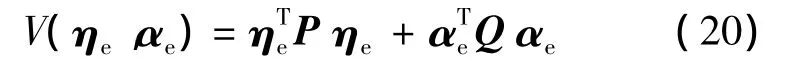
其中，对称矩阵P＞0，Q＞0。对式(20)沿着系统(12)的轨迹求导，并将式(15)代入得

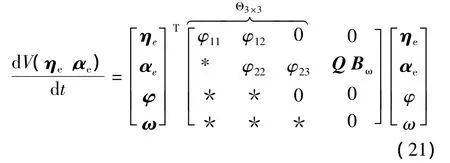
式中:φ11=MTP+PM，φ12=P－BTQ，φ22= (N－B K3)TQ+Q(N－B K3)，φ23=QD。

由式(17)有

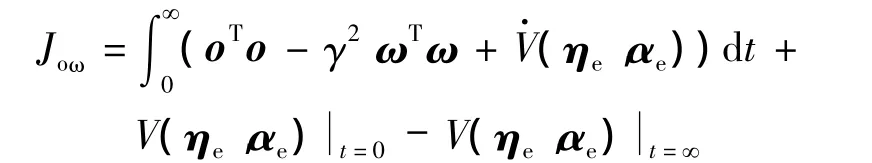
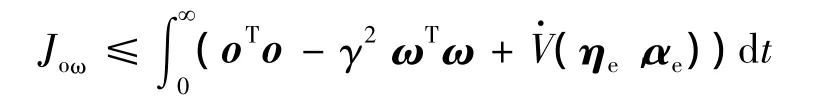
由式(21)可得

由此，若Ξ＜0，那么有Joω＜0，即在零初始条件下，闭环系统具有给定的H∞扰动抑制水平γ。根据S－过程［11］，式(22)＜0成立当且仅当存在对称矩阵P＞0、Q＞0，任意合适维数的矩阵K2、K3和标量ε≥0，使得

成立。其中，Ξ和Γ分别定义于式(22)和式(14)中。

根据Schur补［12］，式(23)等价于:

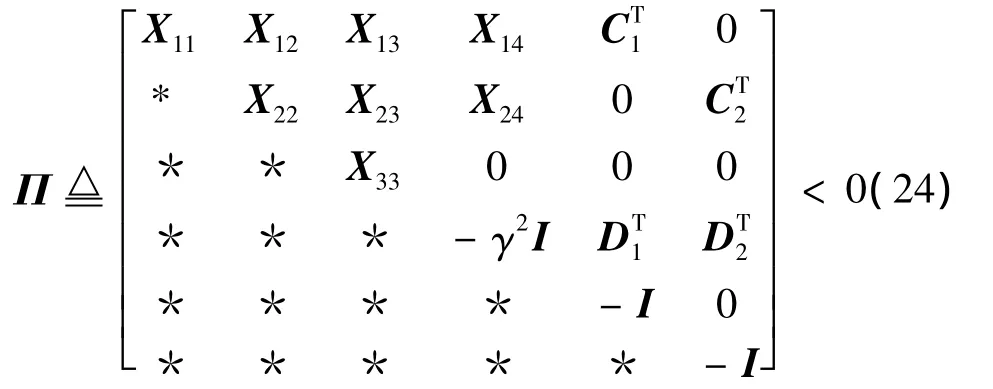
式中:X11=MTP+PM，X12=P－BTQ，X13=－εCTKm，X14=D1，X22=(N－B K3)TQ+ Q(N－B K3)，X33=－2εI，X23=QD+ε CTKm，X24Q B=ω+CT2D2。

观察矩阵Π，若Π ＜0存在可行解，则对应的有χ＜0，χ=[Xij]，i，j=1，2，3存在可行解，观察分别定义于式(21)和式(14)中的矩阵Θ和Τ的形式，则可得Θ+εΤ=χ＜0存在可行解，因而保证了ω=0时标称系统的绝对稳定性。

由于Π中存在决策变量的非线性项，无法直接用LMI工具箱进行求解，所以对矩阵Π做合同变换，分别左乘 diag{P－1，Q－1，ε－1，I，I，I}和右乘diag{P－1，Q－1，ε－1，I，I，I} 。令L1=P－1，L2= Q－1，L3=P－1KT2，L4=Q－1，τ=ε－1有

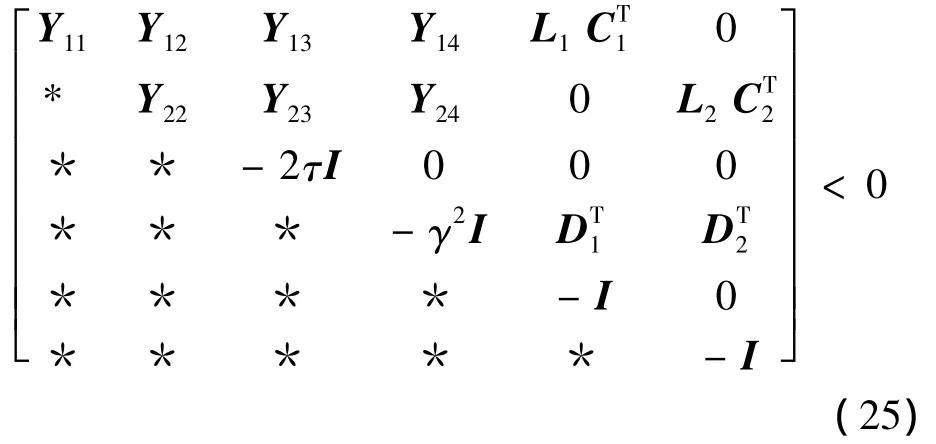
式中:Y11=L1MT+M L1，Y12=L2－L3BT，Y13=－L1CTKm，Y14=L1D1，Y22=L2NT－L4BT+ NL2－B L4，Y23=τD+L2CTKm，Y24=Bω+

至此，得到了H∞绝对稳定控制器约束条件。即对于给定的标量γ＞0，若存在对称矩阵L1＞0和L2＞0，矩阵L3、L4和标量τ＞0，使得式(25)成立，则闭环系统(14)在控制器K1及u=B－1ρ－K2ηe－K3αe下可以实现绝对稳定，且在零初始条件下，具有H∞性能指标γ。其中，K1是使M为Hurwitz矩阵的任意矩阵

3 仿真分析

采用前文设计的控制器进行仿真分析。选择与文献［2］相同的参数值，取V=75m/s，Rn=0.0191 m，R =0.0508 m，Cx0=0.82，n=0.5，σ=0.03，L=1.8 m，g=9.81 m/s2，m=2。为了使M=A1－K1为Hurwitz的，可以利用极点配置方法，取M的极点为[－6+2.7713i －6－2.7713i]，对应的反馈矩阵为。计算得到LMI的一个可行解为令为考虑噪声干扰时，取噪声干扰ω= [ω1ω2]T，其中，ω1=ω2=5sin(2πt)。另外，空化器和尾舵的饱和值分别设为20°和50°，仿真步长设为0.5 ms，经过2 s后，仿真结果如图2和图3所示。如图2所示，标称系统的4个状态在1 s左右能够准确跟踪给定的阶跃指令，受干扰系统的状态的稳态误差在可接受的范围内。在仿真开始时，标称系统与受干扰系统的尾舵偏转角均出现饱和，其幅值受到限制。空化器偏转角最大值为15°，未饱和。

图3给出了正弦指令跟踪响应曲线，从图中可以看出，标称系统与受干扰系统的状态响应曲线几乎重合，均能准确跟踪给定指令。同样，尾舵偏转角在仿真开始也出现饱和。与图2区别在于，由于图3的跟踪指令为正弦深度指令，和阶跃指令相比，正弦指令虽然在仿真初始时的纵向深度指令

仿真过程中初始状态设为z0=θ0=w0=q0=0，分别跟踪阶跃深度指令和正弦曲线深度指令，其中阶跃指令为zd=1，θd=wd=qd=0，正弦曲线深度指，但是由于其俯仰角指令，即，最终导致控制输出幅值变大，所以图3中标称系统和受干扰系统的空化器偏转角在仿真初始均出现饱和。另外，在仿真过程中，空化器和尾舵偏转角均在允许范围内变化。

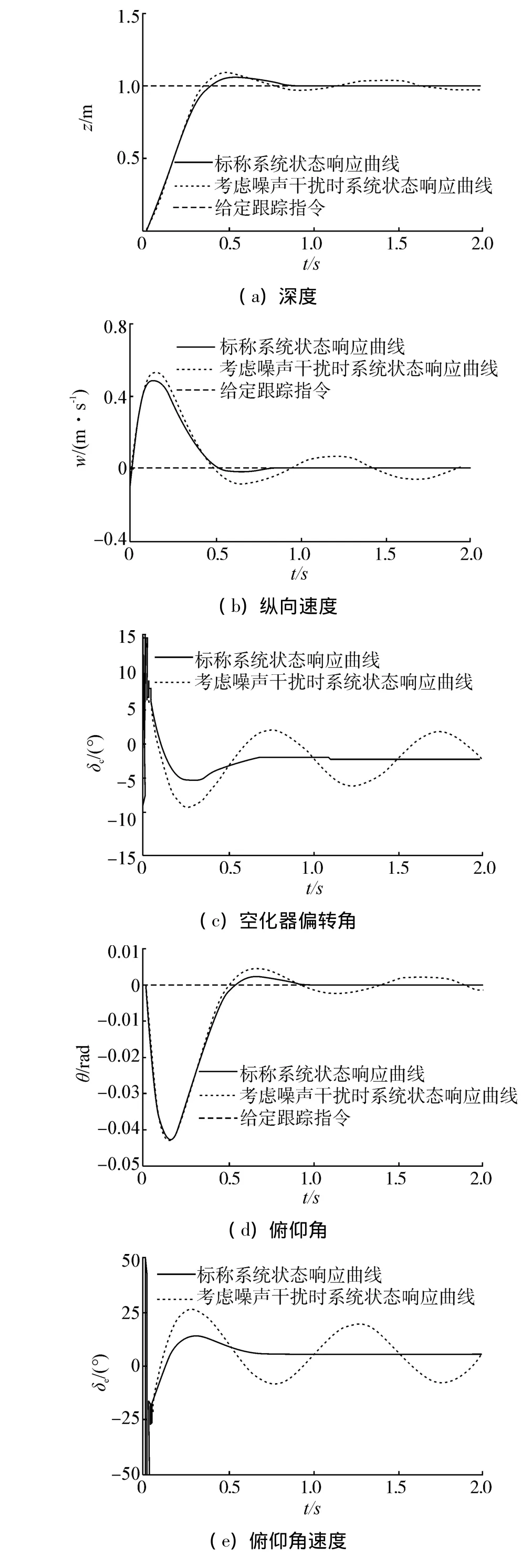
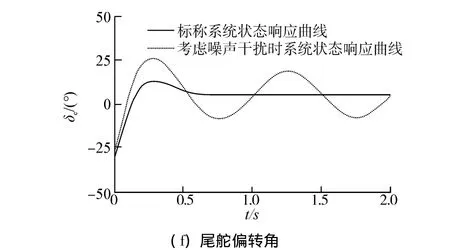
图2 零初始状态阶跃响应曲线Fig.2 z-step input tracking responses under zero initial states

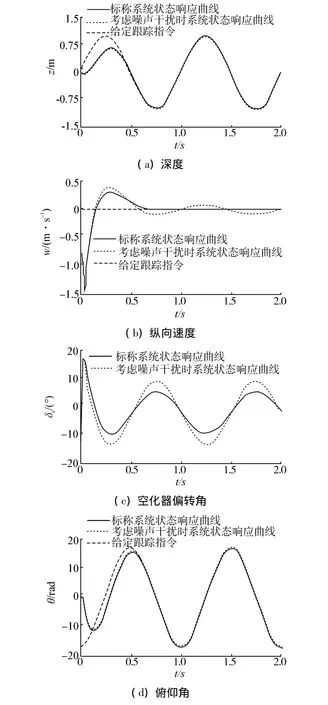
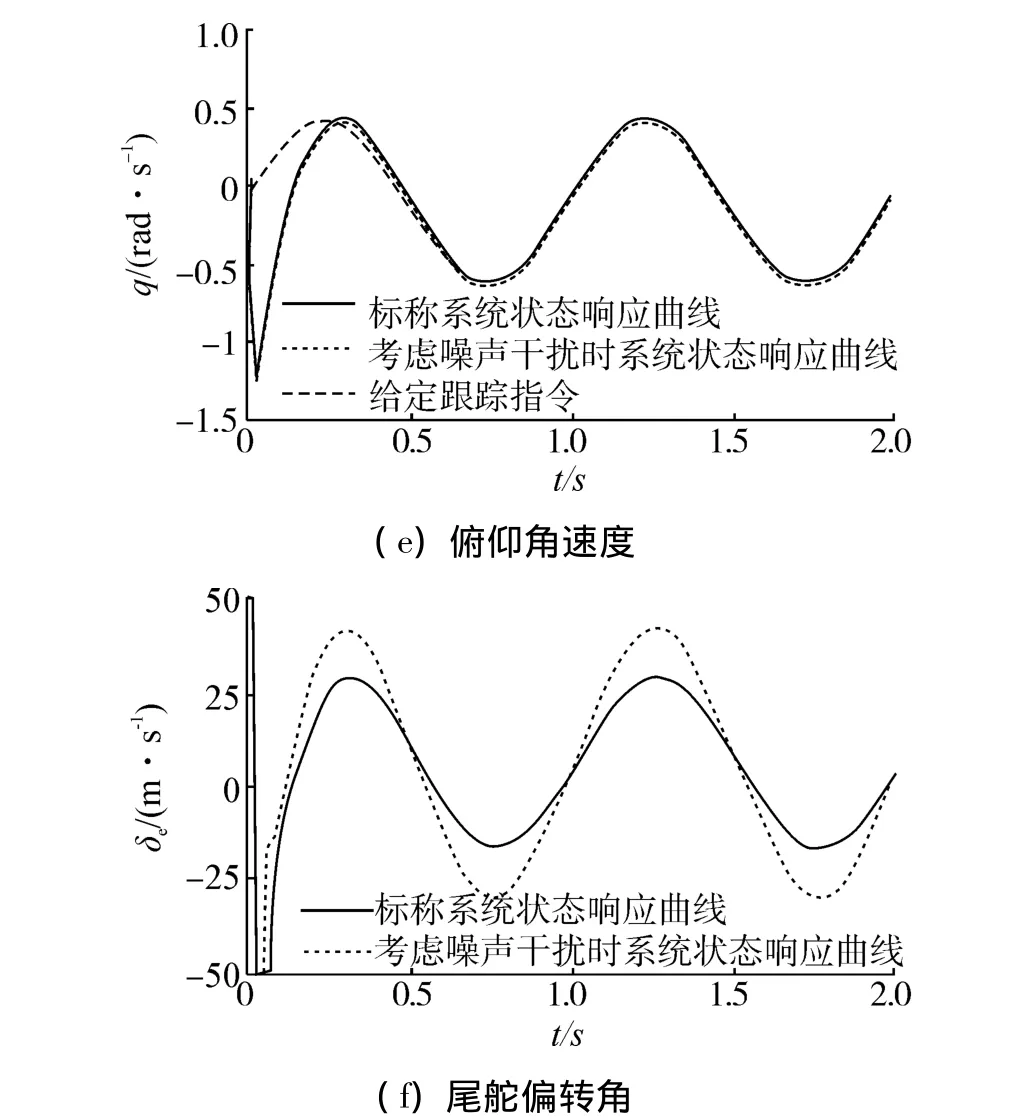
图3 零初始状态正弦响应曲线Fig.3 z-sine reference signal input tracking responses under zero initial states

4 结束语

针对超空泡航行体在航行过程中受到的强烈非线性滑行力和噪声干扰问题设计了鲁棒H∞绝对稳定控制器。仿真中，系统状态能够跟踪给定指令，且误差较小，表明了所设计的控制器的有效性。由于文章只考虑了噪声干扰的影响，因此进一步考虑不确定性对超空泡航行体的影响并设计相应的控制器等问题都有待于研究。

［1］VANEK B，BOKOR J，BALAS G J，et al.Longitudinal motion control of a high-speed supercavitation vehicle［J］.Journal of Vibration and Control，2007，13(2):159-184.

［2］DZIELSKI J，KURDILA A.A benchmark control problem for supercavitating vehicles and an initial investigation of solutions［J］.Journal of Vibration and control，2003，9(7): 791-804.

［3］KIRSCHNER I N，KRING D C，STOKES A W，et al.Control strategies for supercavitating vehicles［J］.Journal of Vibration and Control，2002，8(2):219-242.

［4］KULKARNI S S，PRATAP R.Studies on the dynamics of a supercavitating projectile［J］.Applied Mathematical Modelling，2000，24(2):113-129.

［5］LIN G，BALACHANDRAN B，ABED E H.Nonlinear dynamics and control of supercavitating bodies［C］//Collection of Technical Papers-AIAA Guidance，Navigation，and Control Conference.Reston，USA，2006:3151-3164.

［6］LIN Guojian，BALACHANDRAN B，ABED E H.Dynamics and control of supercavitating vehicles［J］.Journal of Dynamic Systems，Measurement，and Control，2008，130(2): 021003.

［7］范辉，张宇文.超空泡航行器稳定性分析及其非线性切换控制［J］.控制理论与应用，2009，26(11):1211-1217.

FAN Hui，ZHANG Yuwen.Stability analysis and nonlinear switching controller design for supercavitating vehicles［J］.Control Theory and Applications，2009，26(11):1211-1217.

［8］范辉，张宇文.基于圆判据的超空化航行器状态反馈控制研究［J］.西北工业大学学报，2009，27(5):694-700.

FAN Hui，ZHANG Yuwen.A simple but practicable state feedback control method for supercavitating vehicle using circle criterion［J］.Journal of Northwestern Polytechnical University，2009，27(5):694-700.

［9］MAO Xiaofeng，WANG Qian.Nonlinear control design for a supercavitating vehicle［J］.IEEE Transactions on Control Systems Technology，2009，17(4):816-832.

［10］KHALIL H K.Nonlinear Systems［M］.3rd ed.Englewood Cliffs，NJ:Prentice-Hall，2002:264-270.

［11］JAKUBOVIC V A.The S-procedure in nonlinear control theory［J］.Vestnik Leningard University Mathematics，1977，4(1):73-93.

［12］BOYD S，EL GHAOUI L，FERON E，et al.Linear matrix inequalities in system and control theory［M］.Philadelphia:Society for Industrial and Applied Mathematics，1994:21-26.