一种基于聚类分析的短期电力负荷预测方法研究

包晓晖，陈 冲，肖方顺

(1.福建水利电力职业技术学院，福建 永安 366000；2.福州大学 电气工程与自动化学院，福建 福州 350116；3.国网福建省电力有限公司，福建 福州 350003)



一种基于聚类分析的短期电力负荷预测方法研究

包晓晖1，陈 冲2，肖方顺3

(1.福建水利电力职业技术学院，福建 永安 366000；2.福州大学 电气工程与自动化学院，福建 福州 350116；3.国网福建省电力有限公司，福建 福州 350003)

基于数据处理理论，提出将电力负荷历史数据按重要影响因素日子类别及温度区间进行聚类分析的方法，设计一个递归模型，使得短期电力负荷预测函数变成线性问题，并进行MATLAB编程仿真，最后通过算例分析验证了该模型具有较高的可操作性、有效性与预测精确性.

聚类分析；MATLAB；电力负荷预测；数据处理

0 引 言

当前，随着我国电力供需矛盾日益突出、电力工业市场化运营的进一步发展，电力负荷预测越显其重要性，其预测的精确度要求越来越高，这既是电力系统规划的重要组成环节，也是电力系统优化调度的基础工具.由于短期电力负荷预测的重要性，自20世纪80年代以来，国内外许多学者都对其理论和方法进行了广泛而深入的研究.其中，文献[1-2]利用人工智能网络具有较强的非线性映射能力的特点，将人工智能网络引入模糊数学方法进行短期负荷预测，文献[3]中则采用小波分析方法进行非参数化预测，文献[4-5]提出了将模糊逻辑技术和神经网络分别应用于时间序列的改进方法.文献[6-7]则分析了电力短期负荷的众多影响因素，比较了几种不同的预测方法，但明确目前尚无绝对精确的数学模型.

在前述研究的基础上，笔者提出了一种基于数据处理和聚类分析的短期电力负荷预测方法，即对电力负荷的历史数据进行处理，研究其影响因素(本文主要以日子类别和温度区间为例)，对此进行聚类分析，使其负荷数据呈现出很强的共性与表征性，并建立一个递归模型，将电力负荷预测函数由非线性问题变成线性函数，具有更强的可操作性、有效性和更高的精确度.

1 负荷预测问题分析

1.1 关于电力负荷趋势问题

众所周知，电力负荷是一个区域范围内用电设备所消耗的电力或电量的数值，而影响每个用电设备消耗电能多少的因素则很多，例如经济、时间、气候和随机干扰等.显而易见，在电力规划与预测中，应用随机变量来表示电力负荷.

建模时，可记负荷的k次迭代函数为l(k)，均值为r(k)，方差为s2(k).因而，负荷预测问题即为最小误差的未来负荷求值问题，可表示为：

(1)

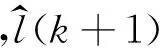
[x-l(k+1)]2=[x-r(k+1)]2+2[x-r(k+1)]
[r(k+1)-l(k+1)]+[r(k+1)-l(k+1)]2

由定义：

E[r(k+1)-l(k+1)]=0

E{[r(k+1)-l(k+1)]=σ2(k+1)

同取期望值：

E{[x-l(k+1)]2}=[x-r(k+1)]2+σ2(k+1)

(2)

由(2)式所知，当令x=r(k+1)时，取得s2(k+1)最小值,即可确定r(k+1))为第k+1次迭代的负荷趋势.

因为负荷可以表示为负荷趋势和一个随机距离的和，则有：

l(k+1)=r(k+1)+w(k+1)

(3)

其中，l(k+1)为负荷，r(k+1)为负荷趋势，w(k+1)为随机距离.

事实上，w(k+1)均值为0，即E[w(k+1)]=0.此外，负荷趋势在每一步的迭代中并非固定，可寻找一个优化函数从而计算出最优未来负荷.

(4)

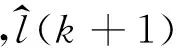
1.2 聚类方法

众知，现实用户中，在不同的日子时电力负荷大小也将有所不同的.譬如，在工作日(多为周一到周五)期间，长期工作制的用电设备会持续运转，负荷功率高且电量大；而在周六周日等休息日，这些企业消耗的电量则有明显的下降.由此，可以根据星期数对电力数据进行初步聚类.对于大多数企事业单位(亦即电力负荷主体单位)而言，星期一是新一周的工作日起始，多数用电设备新启动，起动电流多数较大，可以单独列为一类；对于六天工作制的企业而言，星期六照常工作，但对于电力负荷全局来分析是一个调整的状态，故星期六也可以特殊列为一类；星期日和国家规定的节假日是比较稳定的假期，自当归为一类.由上，可按日子类别对电力负荷进行分类，分为4类，即：星期一；星期二到星期五；星期六；星期日及法定节假日.

再者，在大量的负荷数据分析中，我们发现电力负荷的大小也与温度的高低呈现出极为相似的变化规律.夏季高温时段，民用电器中空调、冰箱等设备的使用几率将上升，生产车间的冷却系统也将投入或增负荷；相反，冬季或低温时，这些用电设备投入少，负荷自当降低.然而，在对电力负荷相关的温度进行分类时，如何进行温度分区是个需特别关注与研究的问题：区间过大，同一类别中数据共性太低，将导致预测数据精确度降低；反之区间过小，聚类将太多，则将导致同类的数据太少，偶然性的数据影响度上升，同样也将影响负荷预测的精确度.本文实验例证中，将温度分为4类，即：[0℃，20℃]；[20℃,30℃]；[30℃，35℃]；[35℃，45℃].

由上，可将日子分成4类，将温度分成4类，所有数据可分成4×4=16类.数据处理时，先将负荷历史数据按该思路分成16类，因为每一类有其相似性与共性，则可分别对每类的历史数据进行聚类分析，得出各自不同的负荷预测函数.当要预测未来某一天或某时刻的电力负荷时，即可根据当天的日子类别和温度区间首先进行聚类分析，然后使用对应的预测函数进行求解计算.

2 模型构建与仿真

2.1 系统建模

如前分析，未来负荷函数可用下式表示：

y(k+1)=a1y(k)+a2y(k+1)+…+
an(k-n+1)+b1x(k)+…bmx(k-m+1)

(5)

最优预测的结果是预测计算值与真实值之间的差距w(k)最小化，故而应选择客观、有效的数据，则：

(6)

qt=[a1,a2,…,an,b1,b2,…,bm]t为参数向量；

X(k+1)=[y(k),y(k-1),…y(k-n+1),l(k),l(k-1),…l(k-m+1)]为包含了负荷预测值与真实值的向量.

为计算预测负荷，需要求出未知的参数变量qt，由上论述，可将误差准则定义为：

(7)

为缩小误差，可以采用递归理论：

y(k)=θ′X(k)

e(k)=l(k)-y(k)

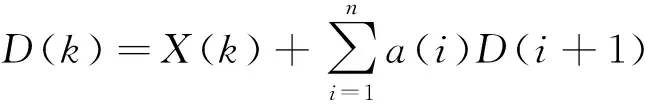
(8)

q=q+αe(k)D(k)

其中，D(k)为y(k)偏导数的一个估计值，0<α<1.

由前述的聚类方法，将数据进行筛选处理，负荷预测则转化成了线性预测，实际上也可以使用最小二乘法拟合一次线性函数.对本文的具体负荷预测问题的一次最小二乘估计公式为：

y(k)=a0+a1k

(9)

其中y(k)为一次预测函数；wk为k的权重系数.

权重系数wk的选取，可根据同类数据的多少确定，取值范围0～1.先由上方程组计算出预测函数系数a0和a1，然后再由预测函数计算出预测值.

2.2 MATLAB仿真设计

MATLAB是一款当今科研、工程领域广泛应用的，集工程计算、系统设计、图形绘制的仿真软件.其提供了用于聚类分析的多个函数，主要有：

(1)直接聚类，利用clusterdata函数对样本数据进行一次聚类，其缺点为可供用户选择的面较窄，聚类效果受一定的限制；

(2)层次聚类，可较为灵活地根据需要聚类细节进行过程处理：①寻找样本两两之间的相似性和非相似性，用pdist函数计算样本之间的距离；②用linkage函数定义样本之间的连接；③用cophenetic函数评价聚类信息；④用cluster函数创建聚类.

(3)划分聚类，根据样本的特性可使用K均值聚类法和K中心聚类法.

基于本文聚类理念，确定将日子类别按直接聚类法，温度区间则按划分聚类法设计程序.程序总体流程见图1，具体程序此略.

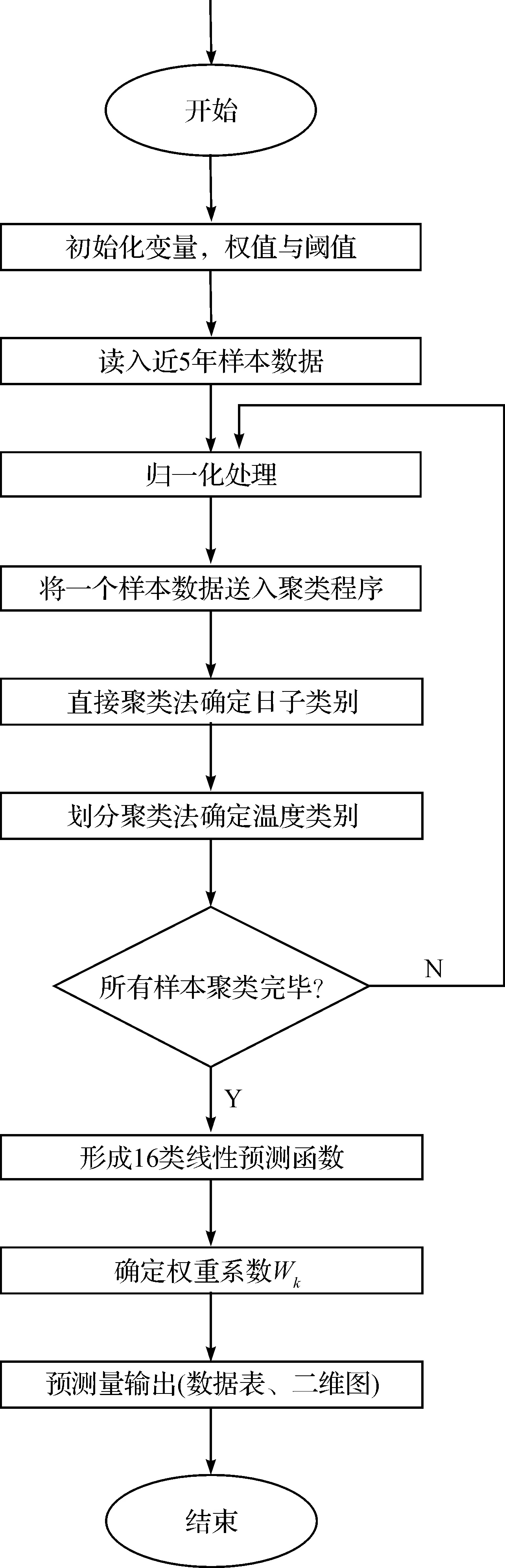
图1 MATLAB程序流程图

3 算例及其误差分析

基于上述建立的预测算法，现引用一年间天气变化显著的某乡镇的供电所2008-2013年共6年的电力负荷数据，并将其前5年的历史数据用作模型的参考数据，第6年数据用来作预测结果的校对.

由上述所设计的MATLAB程序进行归一化分析计算，并将运行结果用二维拟合图形输出.图2为第1年(2008年)各星期一电力负荷与温度的对应关系分析，图3则为5月份中各日电力负荷与温度的对应关系分析.其它日子类型与温度类型组合也有相应的关系分析，由此可见电力负荷与温度相对应的趋势增长关系.

图2 归一化后星期一的电力负荷与温度对应关系

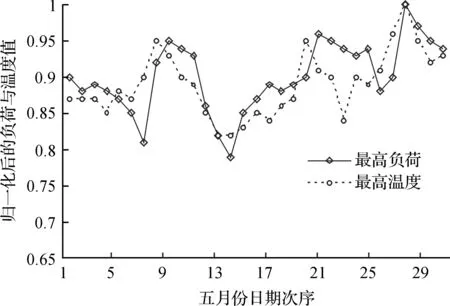
图3 归一化后五月份的电力负荷与温度对应关系

MATLAB程序运行中，利用本文所建聚类分析模型进行第6年电力负荷预测，并将其结果与非聚类分析的其他预测法(本次以公认较精确的“小波分析方法”为例[3])及第6年实际数据进行比较，可得结果(见图4)(以五月份为例).

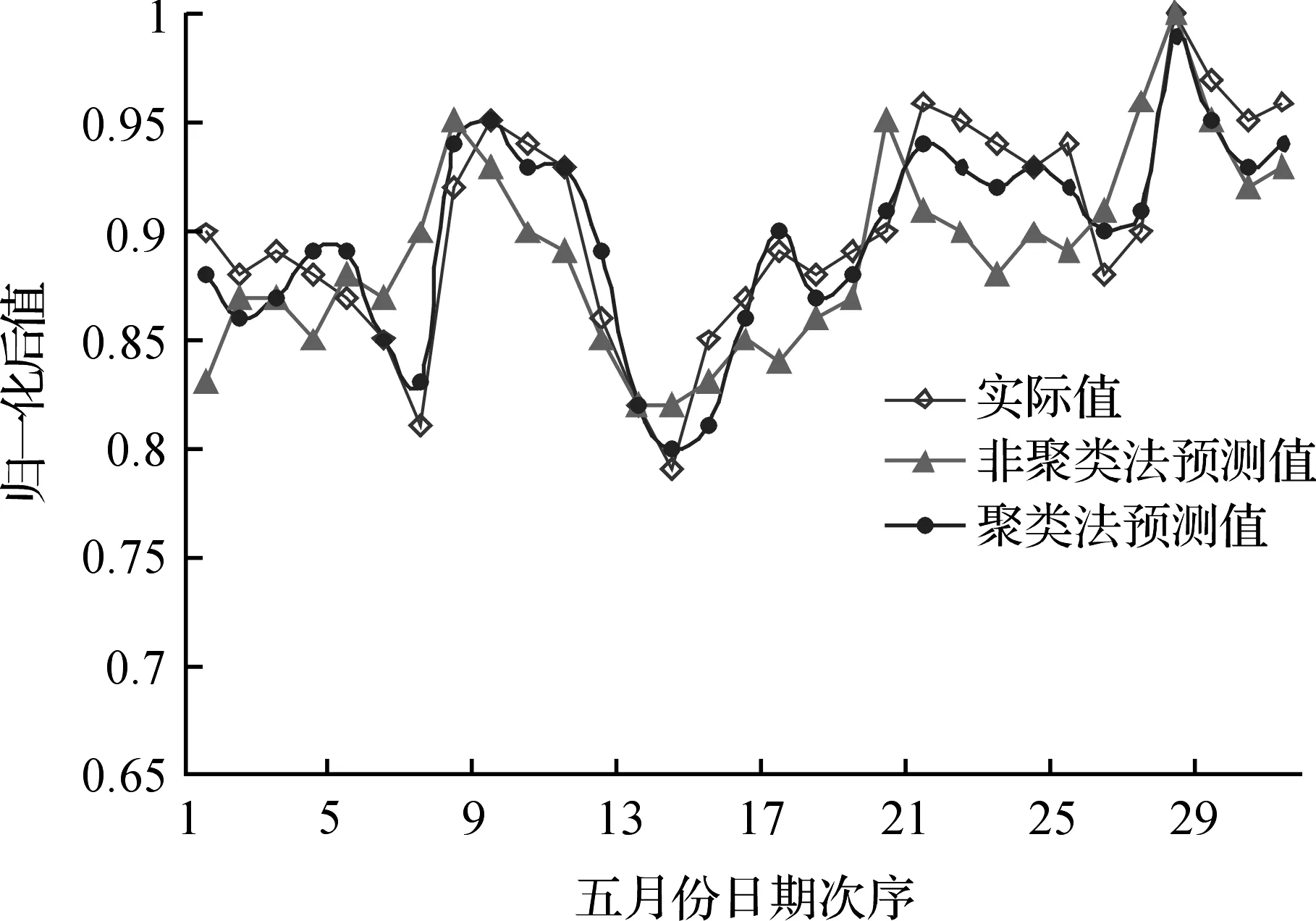
图4 不同方法下的五月份的电力负荷预测

为验证聚类分析预测法的精确性，常采用相对误差(RPE)和平均相对误差(MRPE)两个指标来比较衡量：

(10)

(11)

通过程序计算，可得出非聚类分析预测法(“小波分析方法”为例)最大相对误差(RPE)和平均相对误差(MRPE)分别为4.19%和3.67%，而本文所述聚类分析预测法的误差则为2.81%和2.28%.由此可得如下结论：基于聚类分析的预测模型，预测结果的精确度有明显改善，显示了聚类分析充分利用了历史数据的类型特点，提高预测准确度的能力.

4 结 语

笔者从数据处理理论出发，提出一种基于聚类分析的短期电力负荷预测方法.即将负荷历史数据按日子类别及温度区间进行聚类分析后，因同一类型负荷具有其共性，使得非线性的电力负荷均势转变成线性的预测函数问题，从而提高了可操作性.通过编程仿真、算例分析与比较，验证了本文建立的预测模型具有更高的精确性.

当然，业内对负荷预测方法的研究方兴未艾，本文未能全面对比；此外，关于聚类分析，是否还有更加合理、科学的聚类方案，譬如是否考虑长假、小长假日子类型等；再如按日子的聚类分析可否进一步细化到按小时的聚类分析，对24h负荷进行预测，等，可在本文基础上开展更进一步研究.

[1]LING,S.H.,LEUNG,F.H.F.,LAM,H.K.,etal.Short-termElectricLoadForecastingBasedOneNeuralFuzzyNetwork[C].IEEETransactionsonIndustrialElectronics,2003:1305-1316.

[2] Liao Gwo-Ching Liao,Tsao Ta-Peng Tsao.Integrating Evolving Fuzzy Neural Networks and Tabu Search Forshort Term Load Forecasting[C].Transmission and Distribution Conference and Exposition,2003IEEE PES,2003:755-762.

[3] TRUONG,L.W., WONG,P.K.C.,Modelling and short-term forecasting of dailypeak power demand in Victoria using two-dimensional wavelet based SDPmodels[J].International Journal of Electrical Power and Energy Systems,2008,30(9):511-518.

[4] 王日见，张少华.一种应用时间序列技术的短期电力负荷预测模型[J].上海大学学报(自然科学版)，2002,8(2)：133-136. Wang rijian, Zhang Shaohua, A model for short-term load forecasting based on the time-series[J].Journal of Shanghai University,2002,8(2):133-136.

[5] 张 颖，高中文.基于时间序列和神经网络的电力系统负荷预测[J].哈尔滨理工大学学报，2003,8(1)：30-32.

[6] HO,S.,XIE,M., GOH,T.N.,A Comparative Study of Neural Network and Boxjenkinsarima Modeling in Time Series Prediction[J].Computers and Industrial Engineering,2002(42):371-375.

[7] TAYLOR,J,MCSHARRY,P., DE MENEZES,L..A Comparison of Univariate Methods for Forecasting Electricity Demand up to a Day Ahead[J]. International Journal of Forecasting,2006(22):1-16.

On Short-term Electric Load Forecasting Based on Cluster Analysis

BAO Xiao-hui1, CHEN Chong2, XIAO Fang-shun3

(1.Fujian College of Water Conservancy and Electric Power, Yongan 366000, China; 2.College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116, China;3.State Grid Fujian Electric Power CO., LTD., Fuzhou 350003, China)

A model for cluster analysis on electric load history data is proposed in this paper based on the day type and temperature interval, and a recursive method is designed to make the short-term electric load forecasting function into a linear, which is programmed and simulated with MATLAB. After all, the advantage of the model is tested, proving its operability, validity and accuracy of prediction by case analysis.

cluster analysis; MATLAB; electric load forecasting; data processing

2015-06-20

福建省水利中青年学科带头人基金项目;福建省教育厅科研项目(JB13313).

包晓晖(1974-)，男，福建屏南人，副教授，硕士，主要从事电力系统规划、设备与装置的教学与研究.

TM715

A

1008-536X(2015)09-0073-04