一种基于宽带信号的抽取滤波器设计
2015-03-23李峰
李 峰
(中国电子科技集团公司第20研究所,西安 710068)
一种基于宽带信号的抽取滤波器设计
李 峰
(中国电子科技集团公司第20研究所,西安 710068)
级联积分梳状(CIC)滤波器结构简单,所耗逻辑资源少,广泛用于高速抽取和插值操作,但处理宽带信号的幅频响应不理想,难以满足抗混叠性能。通过分析传统CIC 滤波器结构和功率谱密度,改进型滤波器利用锐化级联积分梳状(SCIC)技术提高阻带衰减并加入内插二阶多项式(ISOP)补偿器降低带内容差,同时讨论了现场可编程门阵列(FPGA)实现的硬件结构和寄存器位宽。仿真验证了改进型滤波器具有更好的通、阻带特性。
级联积分梳状滤波器;内插二阶多项式补偿器;幅频响应;阻带抑制
0 引 言
级联积分梳状(CIC) 抽取滤波器由Hogenauer[1]提出,分解为积分器(递归部分)和梳状器(非递归部分)两部分,其传递函数为:
(1)
式中:N为CIC滤波器级数,决定阻带衰减程度;R为微分延迟,取值为1或2,决定频谱响应中第一零点位置;M为抽取因子,由滤波器输入、输出采样率决定,系数1/(MR) 确保0 dB的直流增益。其对应的频率响应为:
(2)
实现时,可将M倍抽取器提到梳状滤波器之前,使得积分器工作于输入采样率fs上, 而梳状滤波器工作在抽取之后的低采样率fs/M上,整个结构只用到加法器和寄存器,显著降低了硬件资源损耗[2]。
频域上,CIC滤波器的零点位于fs/M(R=1)的整数倍处,抽取操作使得第一零点fs/M附近区域混叠到滤波器通带中,如图1所示。假设信号带宽为fc,要求CIC滤波器的最小通带截止频率为fc,则fs/M-fc处的阻带抑制和fc处的通带衰减决定了滤波器的频域性能。随着fc的增加,幅频曲线中的上述两点逐渐靠近,CIC滤波器性能显著下降。
针对宽带信号,本文利用阻带锐化和通带补偿技术对传统CIC滤波器进行改进。滤波器设计输入:输入采样频率fs为160 MHz,抽取因子M为5,输出采样频率为32 MHz,信号带宽fc为9 MHz。设计指标:通带波动小于1.5 dB,阻带抑制大于50 dB。
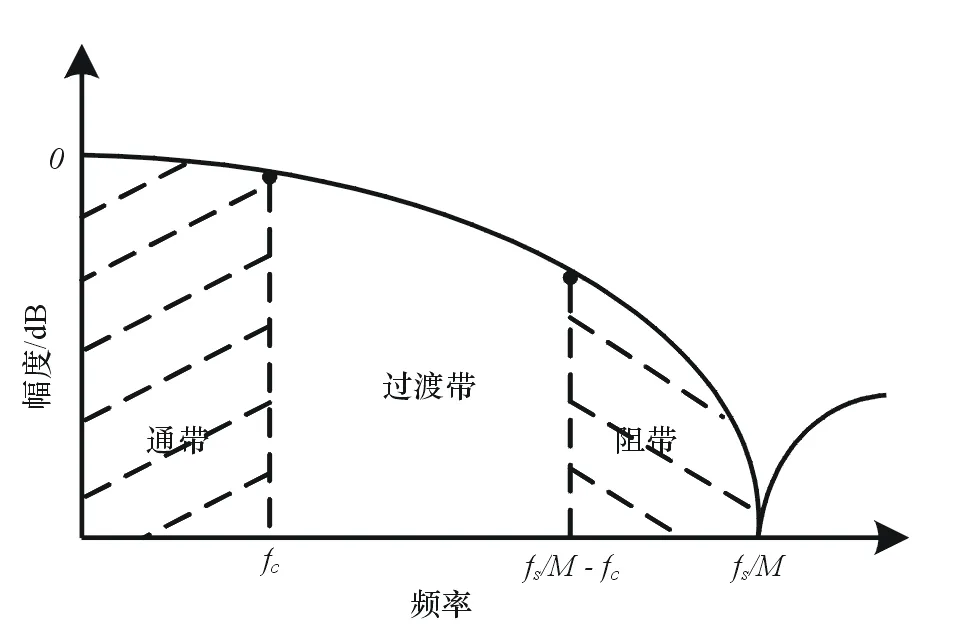
图1 CIC滤波器通带、阻带示意图
1 CIC滤波器的改进
1.1 阻带锐化
通过复用3个基本CIC滤波器,一种名为SCIC的滤波器被提出,既保持了CIC 滤波器“Multip lier - Free”的特点[3], 阻带衰减又得到显著锐化,其传递函数为:
Hsharpen(z)=3H2(z)-2H3(z)
(3)
式中:H(z)为如式(1)所示的基本CIC滤波器传递函数。
图2反映了4种级数SCIC滤波器的幅频曲线,在24~26 MHz之间的4条曲线分别存在一个陷波点,该点位于阻带内,可忽略其对输入信号的影响。由图3可以看出,在相同微分延迟和抽取率的前提下,基本CIC滤波器的级数越高,SCIC滤波器的阻带锐化效果越明显,对于9 MHz的信号带宽,SCIC滤波器采用级数1时,阻带衰减(23 MHz频率点)仅为-40.7 dB,不满足设计要求;采用级数2、级数3和级数4的阻带衰减分别为-59.1 dB、-84.0 dB和-110 dB,级数4的阻带衰减性能最优。考虑通带波动性能,级数3和级数4所对应的通带波动均超过10 dB以上,显著增加了通带补偿滤波器的设计压力;而级数2的通带波动为-6.9 dB,将其补偿至-1.5 dB的设计指标具有可行性。综合通带波动和阻带抑制性能,本文选择级数2的SCIC滤波器。

图2 SCIC滤波器通带波动和阻带抑制
(fs=160 MHz,M=5,R=1,fc=9)
1.2 通带补偿
为补偿通带6.9 dB的波动,在SCIC滤波器之后级联1个内插二阶ISOP滤波器[4],传递函数和频率响应如下:
(4)
(5)
式中:I为正整数,为便于硬件实现,I是抽取因子M的整数倍。
本文设定I=M,系数1/|c+2|用于归一化滤波器的直流增益。当c<-2时,ISOP滤波器的幅频特性在[0,fs/2M]内单调递增,恰好可以对SCIC滤波器的通带衰减进行有效补偿。此外,ISOP滤波器的最小幅度响应位于fs/M的整数倍处,与SCIC滤波器的零点重合,保证了补偿后仍具有混叠抑制特性。
表1统计了SCIC滤波器加ISOP滤波器补偿后,系数c对最大增益、通带波动和阻带抑制的影响。可以看出,当系数c=-3时,通带内过补偿以致出现4.23 dB的正增益,且阻带抑制小于50 dB;随着系数c的减小,通带补偿效果降低而阻带抑制性能有所提高,但提高效果减缓,综合考虑后选择c=-4作为ISOP滤波器的实现方案。
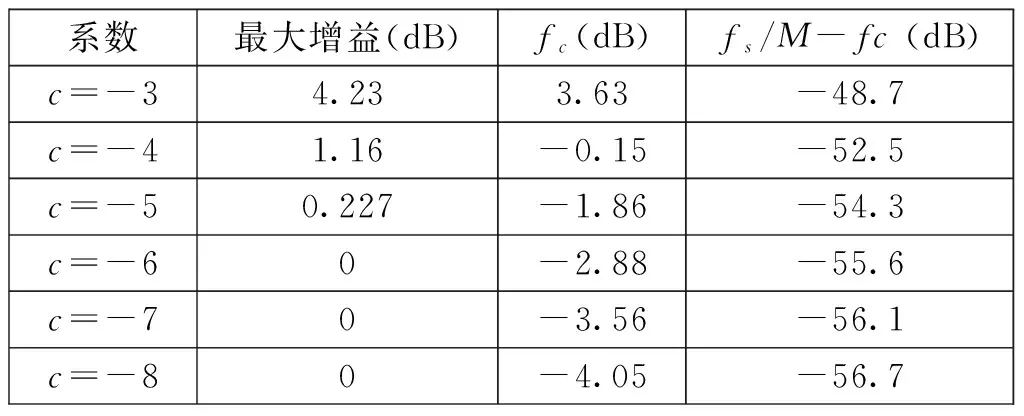
表1 系数c对改进型滤波器的影响(fs=160 MHz,M=5,R=1,fc=9)
图3给出了本文设计的改进型滤波器、SCIC滤波器和传统CIC滤波器的幅频曲线,对比发现:改进型滤波器在通带波动和阻带抑制性能上是SCIC滤波器和CIC滤波器合理的折衷。
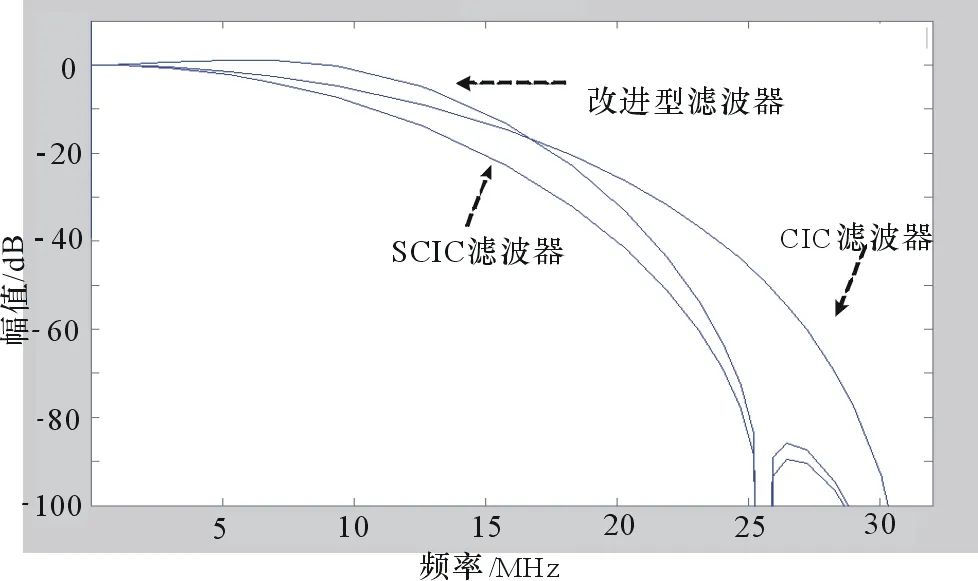
图3 改进型滤波器、SCIC滤波器和传统CIC滤波器幅频曲线(fs=160 MHz,M=5,R=1,fc=9)
2 FPGA实现
2.1 硬件结构
改进型滤波器由SCIC滤波器和ISOP滤波器串联组成,而本文的SCIC滤波器又以2级传统CIC滤波器为基础。暂时不考虑直流增益因素,合并式(1)、式(3)和式(4)得到改进型滤波器的传递函数HADV(z)为:
(1+cz-M+z-2M)
(6)
借鉴传统CIC滤波器实现过程中将抽取器置于积分器和梳状滤波器之间的方法,使得梳状滤波器和ISOP滤波器的系数降低至原系数的1/M,这部分的硬件处理速度也降至原速度的1/M,既便于电路设计又降低硬件功耗。基于这种方法,将式(6)进行调整得到:
式中:中括号内的减法运算使得数据通路中存在2个分支,其中1个分支为2级传统CIC滤波器,单级CIC滤波器群延迟为(M-1)/2,2级CIC滤波器的群延迟为(M-1)[5],在该支路中再加入1个时钟周期的延迟,使得支路延迟变为M,为保证两支路群延迟一致,另一支路中直接引入M时钟周期延迟,并将M倍抽取器置于该延迟单元之前,从而降低支路的运算速度。
通过上述分析,得到改进型滤波器的硬件结构如图4所示。其中1/(1-z-1)和(1-z-1)为传统CIC滤波器的积分和梳状部分,乘(-2)、乘(-4)运算可以利用移位操作实现,乘3运算利用移位加法操作实现,整个滤波器不包含任何乘法电路,为现场可编程门阵列(FPGA)节省了大量逻辑单元。

图4 改进型滤波器的硬件结构
2.2 寄存器位宽
改进型滤波器包含积分运算,即对输入数据不断累加,这要求内部寄存器必须具有合理的位宽,否则中间运算结果会发生溢出。寄存器位宽的设计原则为:保证改进型滤波器在最大增益处不发生溢出。
首先分析改进型滤波器的直流增益,传统CIC滤波器直流增益为(RM)N[6],在此基础上结合式(3)和式(5),得到改进型滤波器的直流增益计算公式为:
(8)
在ISOP滤波器的补偿作用下,如果最大增益发生在直流点,最大增益和直流增益计算公式相同;若ISOP滤波器过补偿,如图3所示,最大增益发生在某一频点,则最大增益在直流增益的基础上乘以一个增量因子KProd,该增量因子可以通过仿真获得,根据表2中c取-4时最大增益为1.16 dB,得到本文改进型滤波器的增量因子等于1.143。依据寄存器位宽设计原则,得到寄存器位宽WREG的计算公式为:
WREG=Win+log2KProd+2Nlog2(RM)+
(9)
式中:Win为滤波器输入位宽。
将前面给出的设计输入代入上述公式中得到改进型滤波器的寄存器位宽为Win+17,即内部寄存器位宽在输入位宽的基础上增加17位。
3 设计验证
采用Verilog语言对图4所示的改进型滤波器进行描述,选用Xilinx公司XC7K325T芯片在Vivado14.3开发环境下仿真综合。滤波器输入、输出位宽12位,内部寄存器位宽29位,输入采样率160 MHz,5倍抽取,设计综合后占用FPGA资源Slice 查找表(LUT) 498个、Slice 寄存器736个。
利用Vivado自带的直接数字频率综合器(DDS) IP核输出4 MHz的正弦信号,同时叠加上23 MHz、29 MHz的噪声,产生如图5所示的不规则信号并送入改进型滤波器。上图将仿真结果用模拟信号形式显示,可以看出,滤波器将23 MHz和29 MHz的高频噪声滤除,保留4 MHz的正弦信号,与原4 MHz正弦信号相比仅幅值减小,减小程度由改进型滤波器在4MHz频点处的增益决定。图5以数字形式的仿真结果显示了滤波器输出信号变化周期是32 MHz,实现了5倍抽取的功能。
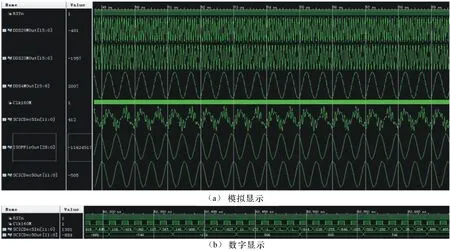
图5 改进型滤波器仿真结果
4 结束语
将SCIC锐化技术和ISOP补偿滤波器相结合,提出了一种改进型抽取滤波器。与传统CIC滤波器相比,该滤波器在通带波动和阻带抑制上得到显著提升。文中推导出改进型滤波器的传递函数,对其分析后提出FPGA实现的硬件结构,并将抽取器置于数据通路的合理位置,降低了部分模块的处理速率,在逻辑资源损耗不变的前提下,有效节省了硬件功耗。仿真综合验证了改进型滤波器满足设计指标要求,使其在通信系统中具有较高使用价值。
[1] Hogenauer E B.An economical class of digital filters for decimation and interpolation[J].IEEE Transactions on Acoustic,Speech and Signal Processing,1981,29(4):155-162.
[2] 杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001.
[3] Dolecek G J,Harris F.Design of CIC compensator filter in a digital IF receiver[A].2008 IEEE International Symposium on Communications and Information Technologies.Vientiane[C].Lao PDR,2008:638-643.
[4] Hyuk J O,Sunbi Kum,Choi Ginkyu,et al.On the use of interpolated second-order polynomials for efficient filter design in programmable downconversion[J].IEEE Journal on Selected Areas in Communications,1999,17(4): 212-217.
[5] 郑瑾,葛临东,李冰.CIC抽取滤波器的改进及其FPGA 的实现[J].信息工程大学学报,2006,7(1): 57-59.
[6] 杜勇,路建功,李元洲.数字滤波器的MATLAB与FPGA实现[M].北京:电子工业出版社,2012.
Design of A Decimation Filter Based on Wideband Signal
LI Feng
(The 20th Research Institute of CETC,Xi’an 710068,China)
Cascaded integral comb (CIC) filters are widely used in high-speed decimation and interpolation operation due to the simple structure and fewer logical resources,but its amplitude-frequency response difficultly meets the anti-aliasing properties in dealing with broadband signals.After analyzing the traditional CIC filter structure and power spectrum density,this paper proposes a modified filter which uses sharpening cascaded integral comb (SCIC) technology to strengthen stopband attenuation and adds intertolated second polynomials (ISOP) compensator to reduce the in-band tolerance,discusses the hardware architecture of field programmable gate array (FPGA) realization and the bit width of register.The simulation verifies that the modified filter has better characteristics of pass-band and stop-band.
cascaded integral comb filter;intertolated second polynomials compensator;amplitude-frequency response;stopband rejection
2014-10-16
TN713.7
A
CN32-1413(2015)02-0093-04
10.16426/j.cnki.jcdzdk.2015.02.024
