基于代理模型和DE算法的天线优化设计

李 哲

(中国船舶重工集团公司第723研究所，扬州 225001)



基于代理模型和DE算法的天线优化设计

李 哲

(中国船舶重工集团公司第723研究所，扬州 225001)

在对天线进行优化设计时，直接使用HFSS等仿真软件进行参数扫描往往需要大量的时间。为解决这一问题，将代理模型法与差分进化(DE)算法相结合，减少了优化过程中的精确电磁仿真次数，显著减少了优化所需时间。随后，使用该方法优化设计了一个准八木天线，结果表明，在10～11 GHz频段内，天线反射系数小于-27 dB，验证了算法的有效性。

差分进化；代理模型；克里金插值

0 引 言

一般的商业电磁仿真软件都能够根据建立好的天线模型给出相应的电磁特性，如阻抗带宽、增益、方向图等。但是，要根据预先设定好的性能指标设计出相应的天线结构与尺寸却不是一件容易的事情。虽然一般的电磁仿真软件都会内置一些参数扫描功能，但直接在电磁仿真软件中进行参数扫描不仅效率很低，而且在面对涉及较多参数的复杂综合问题时，往往难以得到最优化的参数。

由于天线综合问题常常可以归属为黑箱优化问题，各种进化算法的出现使得非遍历寻求最优解在天线设计中成为可能。

与其它进化算法相比，差分进化(DE)[1-2]算法具有简单易用、鲁棒性好、全局搜索能力强、对控制参数的依赖性小的优势，不但在工程实践中得到广泛使用，在国内外进化计算大赛中也屡获殊荣。因此本文选用差分进化算法作为优化算法中的全局搜索引擎。

虽然各种进化算法已经成功应用于天线设计的很多场合，但是在提高天线设计的效率方面，还有很多工作要做。全波电磁仿真在天线设计中常常是必不可少的，然而一组数据的仿真所需要的时间一般从几分钟到十几分钟不等，而一些复杂模型常常需要几个小时到十几个小时。而一个基于进化算法的天线综合问题可能需要上千次计算(电磁仿真)才能找到符合要求的解。显然，如何在不牺牲天线性能的前提下提高进化算法的工作效率成了当务之急。

为了解决上面的问题，本文引入了代理模型法。它使用一个代理模型对所求函数值进行估计，避免了在优化问题中直接对函数值进行精确计算，以减小计算成本。随着在这方面研究的深入，出现了很多优秀的代理模型，例如克里金插值(Kriging Interpolation)[3]，人工神经网络(ANN)[4]，支持向量回归(SVR)[5]，径向基函数(RBF)[6]。与其他代理模型相比，使用克里金插值法建立的代理模型不但具有良好的精度，而且建立时不需要过多的控制参数。最重要的是，它在提供某点的估计值的同时，还能给出估计的误差，这与本文中使用代理模型对新一代个体进行筛选的思想相契合。因此本文使用克里金插值法来建立代理模型。

1 DE算法与克里金插值法简介

1.1 差分进化算法

差分进化(DE)[1-2]算法是一种基于群体差异的启发式随机搜索算法，于1995年由Storn和Price两位学者提出。在连续空间优化问题中，相比其他一些遗传算法，差分进化算法解的质量和收敛速度方面有显著的优势。

与其它进化算法相似，DE算法开始于一个随机选择的初始种群，主要过程包括变异、交叉和选择3个步骤。DE算法的基本流程如图1所示。DE的基本思想是从某一组随机产生的初始种群开始，随机选择2个不同的个体向量相减生成差分向量，将差分向量赋予权值后与第3个随机选择的个体向量相加，产生变异向量。然后将变异向量与预先确定的父代个体向量按一定的规则交叉产生试验向量。若试验向量的适应度值优于父代个体向量的适应度值，则选用试验向量进入下一代，否则保留父代个体向量。通过不断的进化，保留优胜的个体，引导搜索过程向最优解逼近。

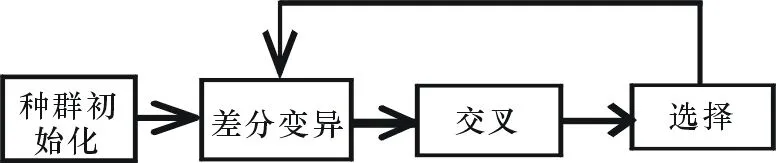
图1 DE算法主要流程

1.2 克里金插值法

克里金(Kriging)插值法[3]又称为空间自协方差最佳插值法，它是以南非矿业工程师D·G·Krige的名字命名的一种最优内插法。克里金插值法广泛地应用于地下水模拟、土壤制图等领域，是一种很有用的地质统计网格化方法。它首先考虑函数值在空间位置上的变异分布并确定对一个待插点值有影响的范围，然后用此范围内的采样点来估计待插点的值。该方法在数学上可对所研究的对象提供一种最佳线性无偏估计。在数据点多时，其内插的结果可信度较高。

这里使用普通克里金法来对一个未知点的值进行估计。这种估计具有以下形式：

fp(x)=μ+ε(x)

(1)

式中：μ为响应函数在周围基点的均值；ε为以0为期望值的误差，误差值以一个相关函数的形式给出，该相关函数由所求点与周围基点的距离确定。

这里使用的是以下形式的高斯相关函数：

(2)

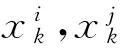
那么，基于克里金插值的代理模型Rs可以定义为：

(3)

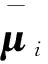
(4)

式中：R0为基点间的相关矩阵：

(5)

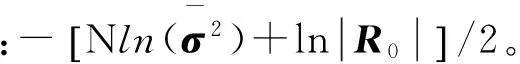
2 代理模型/DE算法

2.1 代理模型/DE算法的核心思想

代理模型法的核心并不是简单的使用代理模型替代电磁仿真来进行适应度计算。要想使用代理模型完全替代电磁仿真来判断一个新个体的好坏，需要代理模型在整个设计空间中具有极高的精确度，而代理模型的精确度越高，需要的采样数据也就越多，在建立模型的时候需要进行更多的电磁仿真。这无疑需要消耗更多的时间，代理模型的优势也就不明显了。如果初始采样点取得太少或是位置不够理想，真实问题的一些特性可能无法在模型中体现出来。

为了解决这个问题，这里并不简单地使用代理模型代替电磁仿真，而是使用代理模型对新产生的子代个体进行筛选，挑选出其中适应度较小的个体，再使用精确电磁仿真对该个体进行验证。也就是说，把代理模型作为一种筛选工具，选出“最有希望”的个体，然后对其进行验证。为此使用置信下限预筛选方法(LCB)[7]。LCB法是基于估计误差的一种筛选方法，它的目的是在可能出现最优解却未被详细探测的区域增加采样点，以弥补仅仅在最初的最优解周围取值所导致早熟的可能性。在克里金插值法中，某个新个体x的预测误差可以用下面的形式描述：

s2(x)=σ2{I-rT(x)R-1r(x)+ [I-rT(x)R-1r(x)]2(ITR-1I)-1}

(6)

根据预测误差，LCB方法使用下面的式子来判断一个新个体的好坏：

(7)

式中：y(x)为使用代理模型计算得到的x的函数值；ω为预先设定好的控制参数。

在LCB方法中，一个个体的ylcb值越小，代表该个体成为最优解的可能性越大。增大ω可以扩大搜索范围，让模型在整个设计空间都有一定的精确度；减小ω可以让算法重点搜索最优解附近的区域，可以增加算法收敛的速度，但却有陷入局部最优解的可能。根据文献[7]的建议，这里取ω=2，以期在全局搜索和局部搜索中取得平衡。

对于每一代的新个体，先使用代理模型计算其适应度值，然后使用LCB方法，按ylcb从小到大对所有新个体进行排序。接着，选取排序后的第1个个体(也就是ylcb值最小的个体)，判断该个体是否已包含在数据库内(如果是，则选取第2个个体，如果第2个个体仍已包括在数据库内，则选取第3个个体，依此类推)，如果该个体未包含在数据库中，则使用HFSS对该个体的参数进行仿真，并将结果加入到数据库中。这样做的好处有：(1)不断有新的仿真数据加入到已有的数据库中，而代理模型是使用数据库建立的，因此代理模型将会越来越精确；(2)每一代只对一个个体进行精细仿真，所需的时间较少。

2.2 代理模型/DE算法步骤

Step1：设置问题的基本参数：包括待优化向量中所含参数的个数n，待优化向量的上下限[Xmin，Xmax]，DE算法的一些参数如尺度因子F，交叉概率RC，种群规模PN，算法终止条件(达到最大代数或是所需要的优化结果)。

Step2：在[Xmin，Xmax]n内随机抽取α个采样点，并使用精确电磁仿真求得其对应的α个响应，在天线综合问题中，这些响应可能是反射系数、增益或是方向性等电参数中的一个。这样就有了一个由采样点和响应构成的原始数据库。

Step3：判断终止条件是否满足，如果满足，则输出数据库中的最好结果；如果不满足，算法继续，进入Step4。

Step4：对数据库中所有的解根据适应度值进行排序，更新目前得到的最好结果，然后取β个最好的解构成一个种群P。这里，β=min(α+G,PN)，G表示当前代数，初始G=0。

Step5：对上一步中产生的种群P进行DE算法的交叉变异操作，产生β个子代向量。

Step6：使用当前数据库中最新的λ个采样点和其对应的响应建立一个代理模型，这里λ=min(α+G,τ)，这里设置τ∈[80,120]，可以根据所优化参数的个数进行调整。

Step7：使用代理模型计算Step5中生成的β个子代向量的适应度值，并使用LCB法对这β个子代向量进行排序。

Step8：记录用LCB法筛选得出的最好的个体，使用精确电磁仿真计算其响应，并将该个体和它对应的响应加入到数据库中去，然后返回Step3。

2.3 代理模型/DE算法的参数设置

(1)DE算法控制参数：包括尺度因子F，交叉概率RC和种群规模PN。根据文献[8]的建议，尺度因子应在[0.4,1]中选取，而交叉概率在区间 [0.5,0.95]中选取比较有效。种群规模根据所优化参数的个数而定，假设要优化的参数为n个，则PN在[4n,10n]的范围内选取比较合适。

(2) LCB控制参数：在使用LCB筛选时，需要设置控制参数ω，根据文献[7]的建议，这里设置ω=2。

(3) 初始化数据库时采样点的个数α，根据所优化问题的复杂程度，α取[4n,8n]比较合适。

3 准八木天线的优化设计

为了验证代理模型/DE算法的有效性，使用该算法优化设计了一个准八木天线。需要优化的准八木天线的结构如图2所示。天线的正面是在金属表面上蚀刻出的微带结构，背面的右半部分覆有金属地板。介质板选用罗杰斯公司的Rogers RT6010，其相对介电常数εr=10.2，厚度为h=0.635 mm。天线使用微带线馈电。

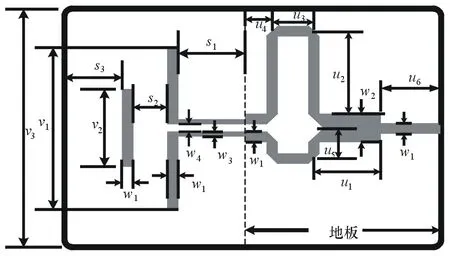
图2 准八木天线结构示意图

需要优化的参数向量为x=[s1s2v1v2u1u2u3u4]，其余的参数由表1给出。表2给出了待优化参数的取值范围。

表1 准八木天线设计参数(单位：mm)

表2 准八木天线待优化参数范围(单位：mm)

优化目的是令该天线在10～11GHz的频段内反射系数尽量小,故优化问题的目标函数可表示为：

(8)

代理模型/DE算法相关的控制参数设置为：初始数据库采样点数α=30，建立代理模型时最大采样点数τ=80。DE算法的基本设置为:选用DE/rand/1策略的标准DE算法，种群规模PN=50，尺度因子F=0.8。交叉概率RC=0.9，进化的最大代数Gm=140。

为了进行准确的电磁分析，采用HFSS和Matlab联合仿真的策略，具体步骤如下：利用 HFSS-Matlab-Api(一种源自于Matlab软件的库函数，能通过脚本接口来控制HFSS)编程，通过该程序生成的VBscript在HFSS中完成天线的模型建立、仿真分析，然后在Matlab主程序中导入仿真结果，这样就可实现对天线精确的电磁仿真。这样，以代理模型/DE算法为优化工具，有效地引导算法寻找最优的天线参数组合；HFSS用来计算天线的电磁性能，完成适应度函数的计算。

图3给出了代理模型/DE算法优化准八木天线的进化曲线图，从图中看出，该算法大约在105代找到了最佳的天线设计参数组合。表3给出优化后的参数。由最佳参数构成的天线的反射系数(如图4)所示，可以看出天线的谐振频率分别为10.2 GHz和11 GHz，反射系数优于-10 dB的带宽为3.2 GHz(8.3～11.5 GHz)，在10～11 GHz的频带内，反射系数优于-27 dB，较好地达到了优化设计的目标。通过上面的例子可以看出，代理模型/DE算法是一种有效的天线优化设计方法。

表3 优化后的准八木天线参数值(单位：mm)

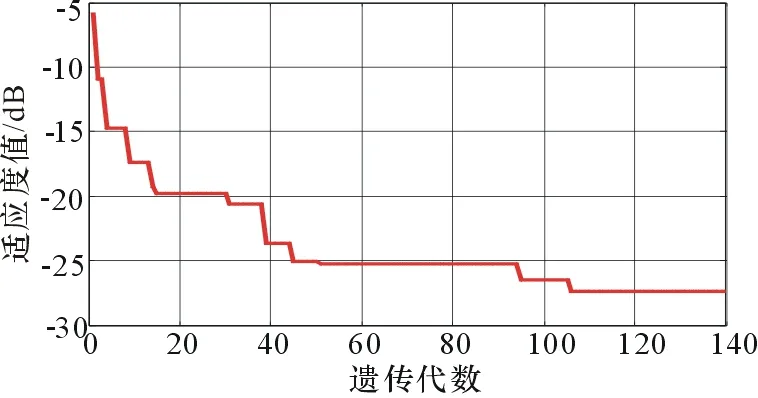
图3 优化准八木天线的进化曲线

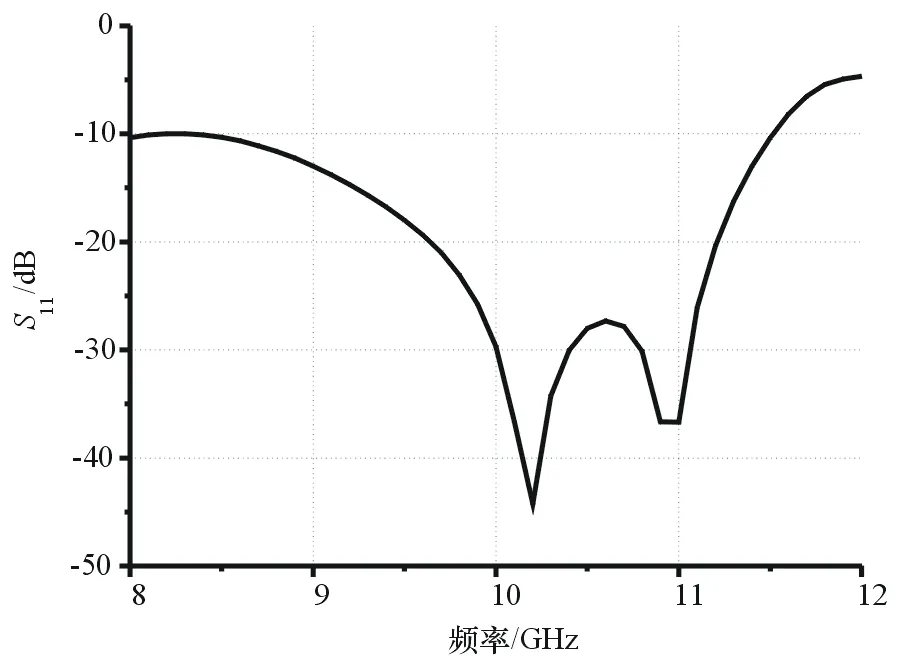
图4 优化后准八木天线的反射系数

4 结束语

本文将代理模型法与DE算法结合，为解决天线优化设计效率低的问题提供了一种新思路。最后使用该方法优化设计了一个准八木天线，从优化设计结果可以看出，代理模型/DE算法是一种有效的天线优化设计方法。

[1] Store R，Price K.Differential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces[M].Berkeley:ICSI,1995.

[2] Store R，Price K.Differential evolution:a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4): 341-359.

[3] Queipo N V,Haftka R T,Shyy W,Vaidynathan R.Tucker P K.Surrogate-based analysis and optimization[J].Progress in Aerospace Sciences,2005,41(1):1-28.

[4] Kabir H,Wang Y,Yu M,et al.Neural network inverse modeling and applications to microwave filter design[J].IEEE Transactions on Microwave Theory and Techniques,2008,56(4):867-879.

[5] Smola A J,Schölkopf B.A tutorial on support vector regression[J].Statistics and Computing,2004,14(3):199-222.

[6] Buhmann M D.Radial basis functions: theory and implementations[M].Cambridge:Cambridge university press,2003.

[7] Dennis J E,Torczon V.Managing approximation models in optimization[J].Multidisciplinary Design Optimization,1997(2):330-347.

[8] 张立.基于差分进化算法的天线优化设计技术[D].西安:西安电子科技大学，2011.

Antenna Optimization Design Based on Surrogate Model and DE Algorithm

LI Zhe

(The 723 Institute of CSIC，Yangzhou 225001，China)

During the optimization design of antennas,directly using simulation softwares such as HFSS,etc.to perform parameter scan may cost a lot of time.In order to solve this problem,this paper combines surrogate model with differential evolution (DE) algorithm,which reduces the times of exact electromagnetic simulation in optimization process so that the optimization time is significantly reduced,then designs a Quasi-Yagi antenna by using this method,the result shows that the antenna reflection coefficient is less than -27 dB within the frequency band of 10～11 GHz,which validates the effectiveness of the algorithm.

differential evolution;surrogate model;Kriging interpolation

2014-09-03

TN823.17

A

CN32-1413(2015)02-0088-05

10.16426/j.cnki.jcdzdk.2015.02.023