矢量叠加算法在相关干涉仪测向中的应用

潘晓霞，杨伟程，杨 杰

(中国电子科技集团公司第36研究所，嘉兴 314033)



矢量叠加算法在相关干涉仪测向中的应用

潘晓霞，杨伟程，杨 杰

(中国电子科技集团公司第36研究所，嘉兴 314033)

采用矢量叠加的方法改善低信噪比情况下相关干涉仪测向性能。在相关干涉仪测向模型的基础上给出了矢量叠加算法流程,根据窄带高斯白噪声的统计特性结合矢量叠加算法流程，理论分析了矢量叠加算法提高信噪比的原理。仿真和试验均验证了该方法的有效性。最后给出了一些对工程实现的建议。

测向；信噪比；高精度；矢量叠加

0 引 言

相关干涉仪测向[1-2]首先通过测量空间来波到达各阵元的相位差，再与各个阵元所有方向的目标信号理论相差进行相关运算得到来波方向，因此相位差的准确度和稳定度直接影响相关干涉仪测向的性能。当信噪比很低时，测向天线阵各单元阵子接收到的来波中噪声分量很大，目标信号的相位差误差明显增大，测得的来波方位误差也同步增大，甚至导致无法测向。假定在一定时间内(矢量叠加算法消耗的时间内)，目标信号的方位保持不变，测向天线阵各单元天线接收到的目标信号相位差是确定的。窄带高斯噪声的包络服从瑞利分布，相位趋近于均匀分布[3]。矢量叠加方法通过多次测量测向接收机各通道之间的相位差(经校正后)和本通道幅度构造信号矢量。将多次测量并构造好的矢量信号叠加后，多次测量的噪声矢量相互抵消，信噪比得到提高，相位差的测量精度和稳定度也得到提高。

1 相关干涉仪模型以及工程实现

1.1 含噪声的相关干涉仪模型

假设测向天线阵由M个阵元构成，布阵方式任意，信号为远场的窄带信号[4]，噪声为高斯白噪声经过窄带系统后的窄带高斯白噪声，信号与噪声统计独立，各通道噪声之间也统计独立，则第m个阵元的输出为：

xm(t)=am(θ)s(t)+nm(t),m=1,2,…,M

(1)

式中：am(θ)=pm(θ)·exp[-jωsτm(θ)],pm(θ)为第m个阵元的幅度响应，ωs为信道的中心频率，τm(θ)为第m个阵元接收信号相对于坐标原点的延时;s(t)为空间信号到达天线阵参考点的复包络;nm(t)为第m个阵元接收的加性窄带高斯白噪声，nm(t)=ρm(t)·exp(ωst)·exp[φm(t)]，ρm(t)和φm(t)分别为窄带高斯噪声的随机包络及随机相位。

将公式(1)写成矢量形式为：

X(t)=As(t)+N(t)

(2)

阵列方向矩阵A具有如下结构：

A(θ)=[a1(θ),a2(θ),…,aM(θ)]T

(3)

对于空间噪声用矢量形式可以表示成：

N(t)=[n1(t),n2(t),…,nM(t)]T

(4)

因此接收机检测到的信息既包含了信号部分,也包含了噪声部分。在时域，单个通道实际接收到的基带信号(零中频信号)矢量[5]表示成：

(5)

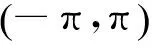
天线阵元接收信号矢量图如图1所示，相位差参考通道窄带高斯噪声矢量图如图2所示。

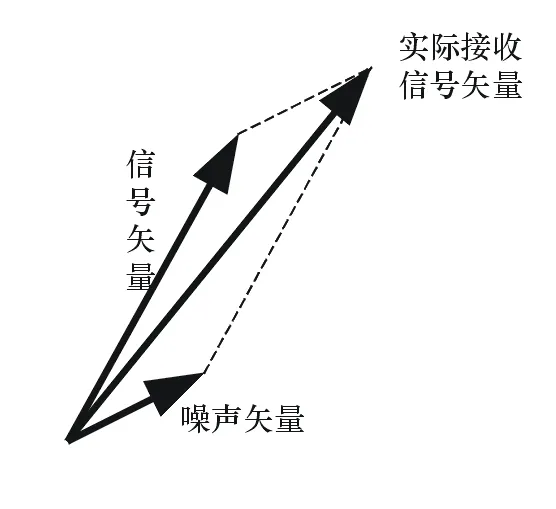
图1 天线阵元接收信号矢量图

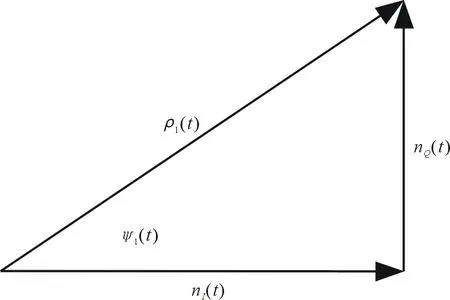
图2 相位差参考通道窄带高斯噪声矢量图

各通道接收信号对参考通道取相差后(又称矢量旋转)，各个通道接收到信号的相差是确定的；假定相位差参考通道的基带噪声表达式为:

(6)

(7)

(8)

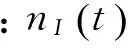
任意通道的基带窄带噪声表达式为：

(9)

(10)

(11)

各个通道对参考相位取相差后的基带噪声表达式为：

ρm(t)·exp{j[φm(t)-φ1(t)]}=ρm(t)cos[φm(t)-φ1(t)]+jρm(t)sin[φm(t)-φ1(t)]

(12)

n″I(t)=ρm(t)cos[φm(t)-φ1(t)]=ρm(t)cos[φm(t)]cos[φ1(t)]-ρm(t)sin[φm(t)]sin[φ1(t)]

(13)

n″Q(t)=ρm(t)sin[φm(t)-φ1(t)]=ρm(t)sin[φm(t)]cos[φ1(t)]-ρm(t)cos[φm(t)]sin[φ1(t)]

(14)

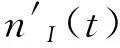
由于窄带高斯噪声是广义平稳且遍历性的[3]，所以工程实现上可以用通过采集一段时间的幅度相位数据，用时间平均值等效统计平均值。时间平均的次数越多，噪声矢量的正交分量和同向分量越趋近于零。由图1可以看出噪声矢量越小，来波信号的抖动就越小，获取的相差稳定度就越高。

1.2 矢量叠加工程实现框图

矢量旋转叠加算法的流程图如图3所示。前端A/D芯片采集数据，快速傅里叶变换(FFT)运算采用quartusII软件自带的IP核。

首先做L点复数FFT运算，并给出多帧(帧数与矢量叠加次数一致)经校正后的窄带信号的幅度和相位数据,送至处理板上的数字信号处理(DSP)芯片。DSP先将相位数据对参考通道取相差，然后将多帧极坐标形式的幅度和相位矢量转成实部和虚部进行累加取平均，最后将矢量平均完的虚部和实部求取出的相差数据进行相关干涉仪测向。

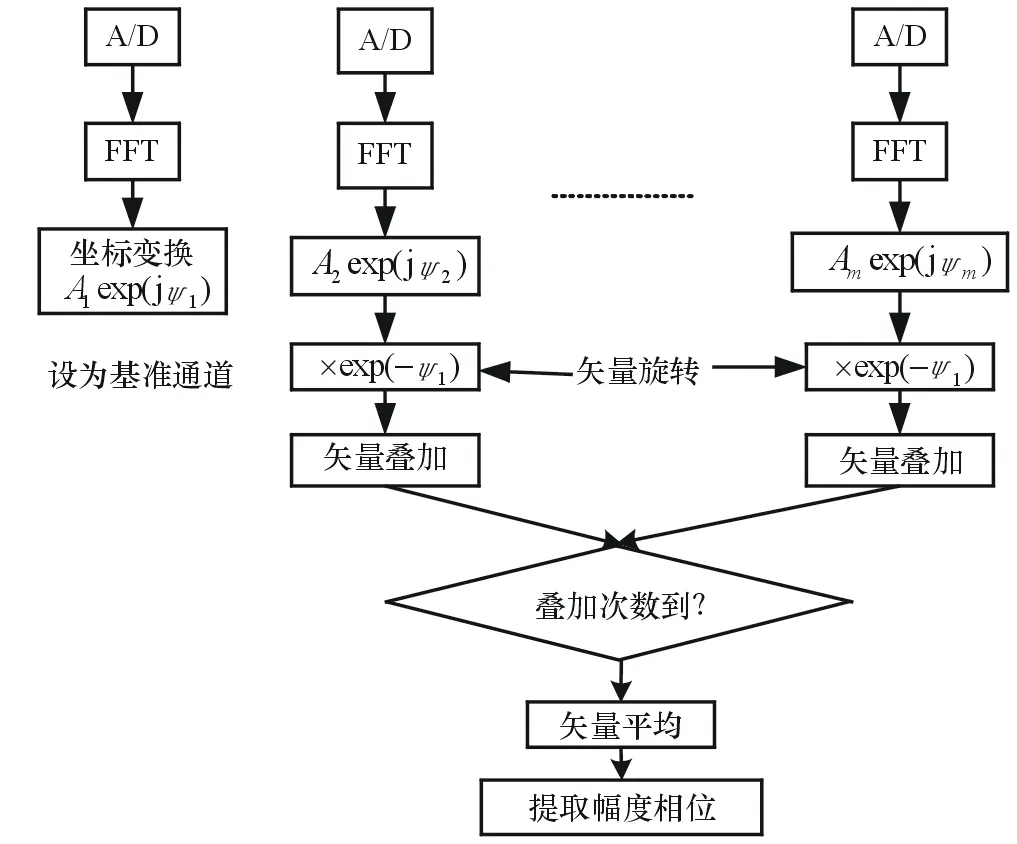
图3 矢量旋转叠加算法的流程图

2 仿真分析

Matlab仿真条件：噪声是零均值、单位方差的伪随机序列。信号为随机初始相位、单位幅度的正弦信号。假定系统调谐器的中频为70 MHz，采样率为56 MHz,矢量叠加前的信噪比约为23 dB,采样序列的长度为1 024个点,天线阵为五元均匀圆阵，半径为0.5 m。仿真结果表明，10次矢量叠加后信噪提高到了37.2 dB，32次矢量叠加后信噪比提高约为14 dB。矢量叠加的降噪效果仿真如图4、图5所示。由图5可见，增加矢量叠加次数有助于提高信噪比，但随着矢量叠加次数的增加，这种作用逐渐变得不明显。工程实践中综合考虑算法消耗时间与信噪比提升程度，可以选择进行16次、32次矢量叠加。

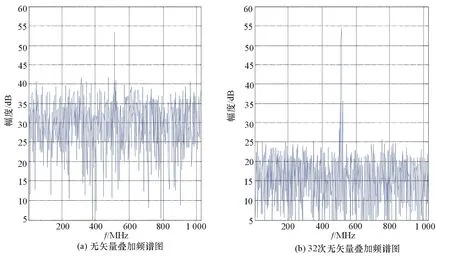
图4 32次矢量叠加前后信号频谱

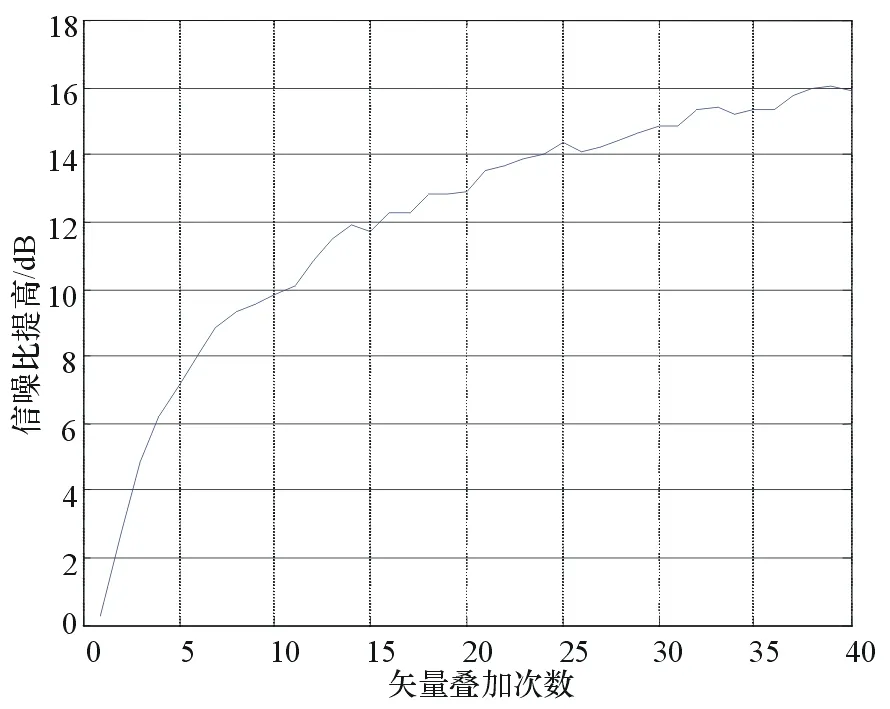
图5 信噪比提高值与矢量叠加次数关系仿真结果图

3 矢量叠加测向试验

将矢量叠加算法用DSP实现后，利用某单机设备以及某系统设备对矢量叠加进行了测向效果对比试验。试验分成2个部分：(1)室内用某单机设备和信号模拟器进行测向对比试验，如图6所示；(2)在空旷场地用某系统设备进行测向效果对比试验，如图7所示。

图6 室内模拟器试验框图

图7 场地试验框图

3.1 矢量叠加测向效果直观展示

室内用某单机设备和信号模拟器进行测向对比试验,矢量叠加对测向影响的直观结果展示如表1。在相同信噪比条件下，随着叠加次数的增加，测得的方位更接近真实方位。

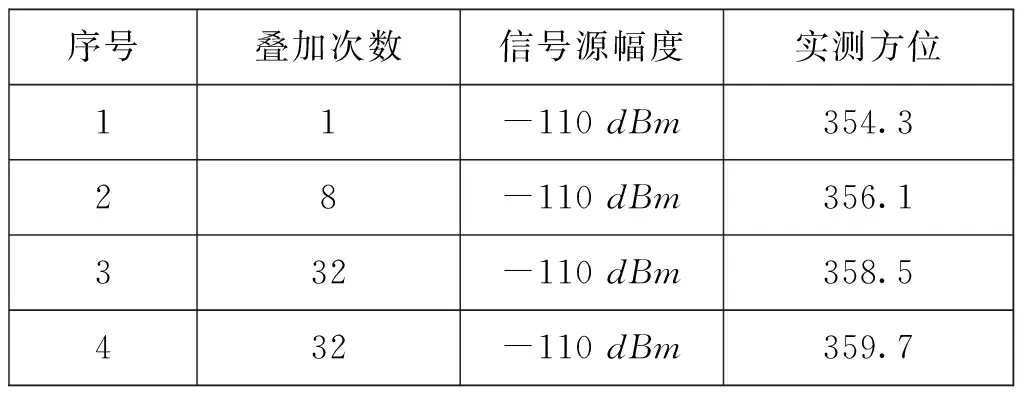
表1 矢量叠加测向结果比对表(频率300 MHz,方位0°)

3.2 场地试验数据分析矢量叠加对测向灵敏度、精度和相位差稳定度的影响

将某设备架设在空旷场地做试验，选取了365 MHz，565 MHz，765 MHz，955 MHz这4个频率点，方位上选取了80°、125°、170°和310°这4个方位，矢量叠加次数统一设定为32次。全面分析了矢量叠加对测向精度和测向灵敏度的影响。

3.2.1 矢量叠加对测向灵敏度的影响

为了验证矢量叠加方法的有效性，本文采用设备接收到的信号大小来表征测向灵敏度。场地试验过程中，不断降低与发射天线相连的信号源所发信号大小(信噪比不断恶化,该设备典型测向灵敏度为8～10 dB)直到系统无法测向(20次测向结果融合值发散)。表2统计了32次矢量叠加相对于不叠加时，设备接收到的第一通道信号大小差值。

场地实测数据表明矢量叠加对不同频率不同方位来波的测向灵敏度均有明显的提高。

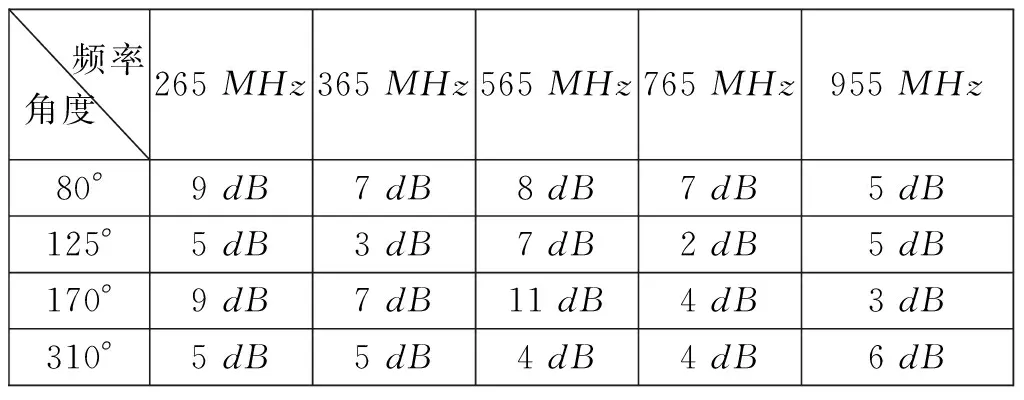
表2 接收机测得的第一通道信号幅度大小差值(场地实测数据)

3.2.2 矢量叠加对测向精度的影响

图8中，横坐标0～3点的位置分别代表定频信号的频率是365 MHz，565 MHz，765 MHz和965 MHz。场地测向数据的统计分析表明,在相同信噪比情况下，不同方位、不同频点的定频信号，32次矢量叠加测向的精度相对于单次测向均有很大程度的提高。

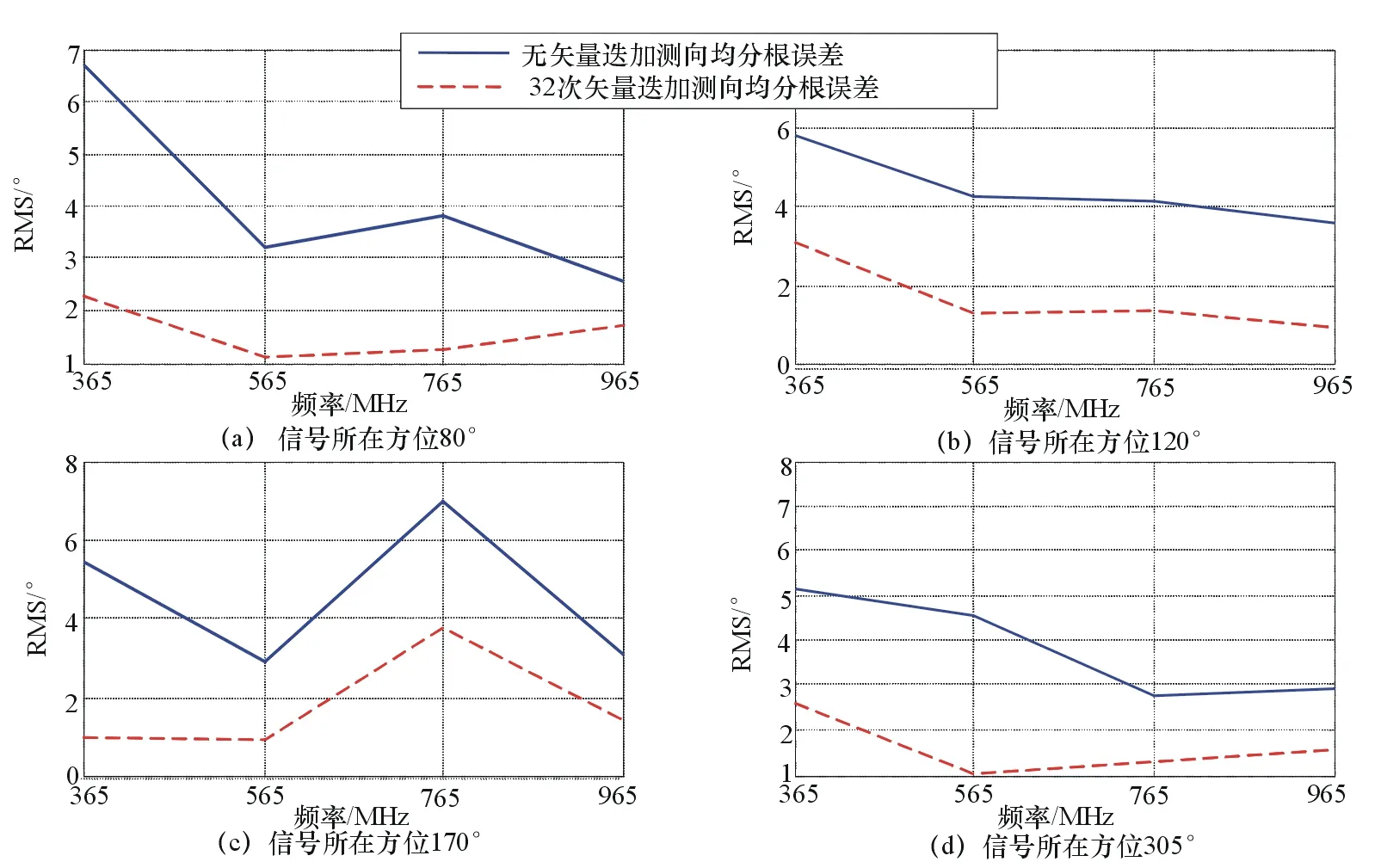
图8 矢量叠加对测向精度影响(场地实测数据分析)

4 结束语

Matlab仿真、模拟器试验以及场地试验均表明，采用矢量叠加算法后，测向灵敏度以及测向精度均有大幅提升。但是该方法也具有一定的局限性，它要求在矢量叠加算法消耗的时间内目标信号的方位具有稳定性。工程实现时可以通过降低算法消耗的时间来解决该问题。

[1] 刘芬，明望，陶松.相关处理在干涉仪测向中的应用[J].电子科学技术评论,2005(6)：31-33.

[2] 张智锋,乔强.低信噪比下相关干涉仪测向处理方法[J].舰船电子对抗,2009,32(6):103-106.

[3] 冯玉珉，张树京.通信系统原理[M].北京：清华大学出版社，2003.

[4] 李淳,廖桂牛，李艳斌.改进的相关干涉仪测向处理方法[J].西安电子科技大学学报，2006，33(3)：400-403．

[5] 杨小牛，楼才义，徐建良.软件无线电[M].北京：电子工业出版社，2001.

Application of Vector Accumulation Algorithm to Correlation Interferometer DF

PAN Xiao-xia,YANG Wei-cheng,YANG Jie

(No.36 Research Institute of CETC,Jiaxing 314033,China)

This paper uses the method of vector accumulation to improve the performance of direction finding (DF) of correlation interferometer,presents the algorithm flow of vector accumulation based on correlation interferometer DF model,according to the statistical characteristic of narrowband Gaussian white noise and the algorithm flow of vector accumulation,theoretically analyzes the theory to improve signal-to-noise ratio (SNR) by vector accumulation algorithm.Both the simulation and test prove the validity of the method.Finally some advices for engineering implementation are proposed.

direction finding;signal-to-noise ratio;high accuracy;vector accumulation

2014-12-24

TN911.25

A

CN32-1413(2015)02-0063-04

10.16426/j.cnki.jcdzdk.2015.02.017