基于粒子群优化的锅炉燃烧过程控制
2015-03-23敖培等
敖培等
摘要:为了克服在对锅炉燃烧过程进行控制时传统控制参数整定方法费时且不能保证获得最佳的性能的问题,本文提出一种基于粒子群优化的锅炉燃烧控制方法,即以各系统误差性能指标ITAE和为适应度,运用PSO自动获取各控制器最优参数。仿真结果表明,采用本文方法可以使整个系统达到较好的控制性能。
关键词:粒子群算法 Simulink建模 锅炉燃烧过程
中图分类号:TM715 文献标识码:A 文章编号:1007-9416(2014)11-0010-01
1 引言
锅炉是化工、炼油、发电等工业生产过程中必不可少的重要动力设备。锅炉燃烧过程自动控制的基本任务是既要提供热量适应蒸汽负荷的需要,又要保证燃料的经济性与锅炉运行的安全性。在对锅炉燃烧过程进行控制时,蒸汽压力控制系统、燃料空气比值控制系统和炉膛负压控制系统三个子系统互相影响,传统控制参数整定的方法费时且不能保证获得最佳的性能。本文提出一种基于粒子群优化的锅炉燃烧控制方法,即以各系统误差性能指标ITAE和为适应度,运用PSO对在建立好的Simulink控制系统模型进行各控制器参数的优化。仿真结果表明,采用本文方法,可以自动的确定控制器最优参数使整个系统达到较好的控制性能。
2 基于粒子群算法的控制器优化
目前,对于控制器参数主要是人工调整,这种方法不仅费时,而且不能保证获得最佳的性能。PSO已经广泛应用于函数优化、神经网络训练、模式分类、模糊系统控制以及其他应用领域[1]。这里首先在Simulink中建立控制系统模型,然后运用PSO进行控制器参数的优化设计,误差性能指标选择ITAE,并以ITAE值作为PSO的适应值。优化过程如下:PSO产生粒子群(可以是初始化粒子群,也可以是更新后的粒子群),将该粒子群中的粒子依次赋值给控制器的参数,然后运行控制系统的Simulink模型,得到该组参数对应的性能指标,该性能指标传递到PSO中作为该粒子的适应值,最后判断是否可以退出算法。算法流程如下:
Step 1: 初始化粒子群,随机产生所有粒子的位置和速度,粒子依次赋值给Simulink模型中的控制器参数,运行控制系统模型,根据返回的适应值确定粒子的最优位置和整个粒子群的最优位置。
Step 2: 对每个粒子,将其适应值与该粒子所经历过的最优位置的适应值进行比较,如较好,则将其作为当前的最优位置。
Step 3: 对每个粒子,将其适应值与整个粒子群所经历过的最优位置的适应值进行比较,如较好,则将其作为当前整个粒子群的最优位置。
Step 4:按照式vt+1=wvt+c1r1(Pt-xt)+c2r2(Gt-xt)和xt+1=xt+vt+1更新粒子的速度和位置。
Step 5:如果没有满足终止条件,则返回Step2;否则,退出算法,得到最优解。
3 基于粒子群的锅炉燃烧控制
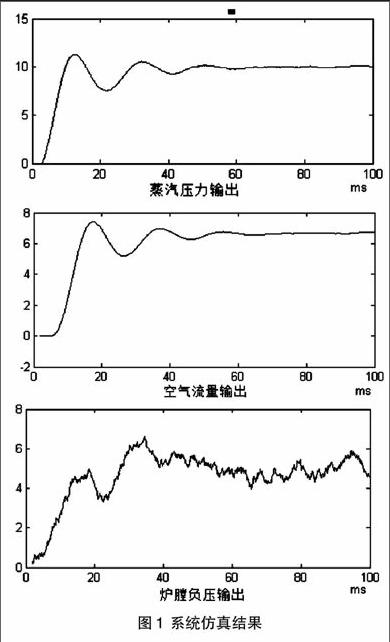
锅炉燃烧过程控制系统主要包括三个互相影响的控制任务,即:维持锅炉汽压、保持最佳空燃比和保证炉膛负压不变。这里参照文献[2]考虑包括蒸汽压力串级控制系统、燃料空气比值控制系统和炉膛负压前馈-反馈控制系统三个子系统的燃烧控制系统。在Simulink中建立系统模型。蒸汽压力设定值和炉膛负压设定值分别为10和5,系统施加幅值为0.2的随机干扰。待整定的控制器参数包括蒸汽压力串级控制主、副回路中PI控制器的Kp和Ki;燃料空气比值控制系统中PI控制器的Kp和Ki;炉膛负压前馈-反馈控制系统中前馈控制器的Kd、T1和T2以及反馈PI控制器的Kp和Ki。采用第2节的方法对各控制器参数进行优化,适应度为三个子系统输出ITAE的和。PSO参数设置如下:惯性因子为0.6,加速常数分别为2和2,粒子群规模为100,最大迭代次数为100,最小适应值为0.1,粒子群速度限定在[-1,1]之间,仿真结果如图1所示。得到最优控制器参数值如下:蒸汽压力串级控制主、副回路中PI控制器的参数分别为KP=0.2,Ki=0.04和Kp=0.55,Ki=0.07;燃料空气比值控制系统中PI控制器的Kp=0.8,Ki=0.08;炉膛负压前馈-反馈控制系统中前馈控制器的Kd=0.13,T1=7,T2=3,PI控制器的Kp=0.01,Ki=0.0015。从仿真结果可以看出,采用本文方法可以自动的调整各子系统控制器的参数,获得较好的控制性能。
4 结语
本文提出一种基于粒子群优化的锅炉燃烧控制方法,即以各系统误差性能指标ITAE和为适应度,运用PSO对在建立好的Simulink控制系统模型进行各控制器参数的优化,以克服在对锅炉燃烧过程进行控制时传统控制参数整定方法费时且不能保证获得最佳的性能的问题。仿真结果表明,采用本文方法可以自动的确定控制器最优参数使整个系统达到较好的控制性能。
参考文献
[1]周碧英.粒子群优化神经网路算法在非线性系统辨识中的应用研究[J].计算机与数字工程,2013,41(8):1220-1221.
[2]刘文定.王东林编著.过程控制系统的MATLAB仿真[M].北京:机械工业出版社,2009.