连云港海域极值波高统计资料年限初探

曹兵，徐常三，高清清，高鑫鑫

（国家海洋局南通海洋环境监测中心站，江苏 南通 226002）

海浪的研究有着极为重要的现实意义，在海岸和海洋结构物的工程设计与建设中都必须考虑设计波高，因为它关系到恶劣海况条件下工程结构物的安全度，以及结构物的造价等问题。同时，极值波高的统计研究对风暴潮的计算、对海岸及沙滩的侵蚀等问题也具有十分重要的意义。当前，江苏省沿海大开发已列入国家战略，连云港海域极值波高统计方法的研究对连云港沿海重大工程，乃至整个江苏沿海的建设都具有十分积极的作用。

目前，国内外很多学者和专家针对极值波高开展了大量的研究工作，并取得了丰硕的成果（You 2003；You，2005；You，2006；Smith，1986；C Guedes et al，2004；王志旭，2013）。但研究主要从设计波高标准、分布函数、拟合线性、参数估计、数值模拟、采样方法等角度研究极值波高，而对资料的使用年限问题研究较少。

S.王等（1984）通过研究发现了在一定置信水平下不同重现期所需最少资料年限等结论，但这些年限是否适于与连云港乃至整个中国沿海，需进一步讨论。

在很多国内外规范和作业指导书（海港水文规范，2013）中，都规定在进行波高或周期的频率分析时，连续的资料年数不宜少于20 a，但对具体设计标准所应采用的具体年数并未定论。

曹兵等（2006；2007a；2008；2014）利用澳大利亚悉尼16 a 连续波浪资料和连云港连续51 a连续波浪观测资料，对采样方法、分布函数进行了较为系统的研究，并得到了初步结论。采样方法方面，研究发现使用年N 大波法最优，其次为波高阈值法，再次为年最大值法。其中，年N 大波法指取每年前N 个最大波，从而既保证了样本容量，又使得每年极值波高数为一常数。这个常数减少了分布函数中的一个变量，使得计算结果误差的变化范围减小。分布函数方面，规范（海港水文规范，2013）推荐使用皮尔逊Ⅲ型分布函数，但此方法参数确定时任意性较为明显。研究发现，Gumbel 分布函数与三参数Weibull 分布函数结果要比对数正态分布函数和皮尔逊Ⅲ型分布函数结果更为可信，三参数Weibull 分布函数则更优。同时发现，在连云港海域最优组合方式为每年取8 个大波和三参数Weibull 分布函数拟合。

在之前研究基础上，本文利用连云港不同资料年限（11～51 a，11 a 为2001-2011年，12 a 为2000-2011年，……，51 a 为1960-2011年全部资料），共计41 组情况，进行了计算与分析，研究更优的资料年限，另外研究了可以满足精度要求的最少年限等问题。

1 资料情况

本文波浪资料采用国家海洋局连云港海洋环境监测站，该站波浪观测人工站位于连云港西连岛北侧，自动观测仪位于连云港西连岛北侧1 km 附近海域（图1），布放处水深约6 m（理论最低潮面），实际水深在9 m 左右，观测浮标直径为1 m。

波浪观测海域位于海洲湾南部，此处海域开阔，水深较浅，地形相对平缓，海底等深线主要为西北-东南向。受东、西连岛影响，波浪资料能较好地反映偏西至偏南向的波浪，西南向波浪影响较大。根据历史资料统计，该海域主要以北到东北、东南风为主，对应的浪向亦是如此，因此波浪资料能较好地反映该海域的实际情况。

图1 连云港波浪观测所在海域示意图

本文使用了1960-2011年（缺少1964年资料）累计51 a 长期波浪观测资料。其中，1960年至2005年为人工观测资料，2006-2011年为人工观测与遥测重力测波仪自动观测相结合的资料。

根据资料统计，热带气旋、温带气旋和冷空气等天气系统对该海域都有影响，因此极值波高在多种情况下都有发生。根据实测波浪资料统计，该海域波型主要为风浪，其次为以涌浪为主的混合浪，以风浪为主的混合浪、涌浪、风浪与涌浪并列的混合浪均存在。

正常天气情况下，人工观测为每日4 次（即08时、11 时、14 时、17 时），自动观测仪每日8 次（即02 时、05 时、08 时、11 时、14 时、17 时、20 时、23 时）。当发生重大海洋灾害过程时，人工观测加密至每小时1 次。需说明的是，使用的波浪数据基于实测资料，而人工观测资料只在白天进行，部分资料会缺失，造成一定的失真，在此次研究中未使用历史天气数据、风等资料进行反演，从而可能会使得结论有一定的偏差，但总体对研究结果影响不大。

人工观测获得的数据为显著波高（即H1/10），自动观测仪获取的资料有显著波高和有效波高（即H1/3）等，为保持资料的连续性和可用性，本课题所用的资料均采用显著波高。

通过设置阈值的方法（曹兵，2014），可得到连云港站51 a 内所有大于阈值的极值波高，也就是本文所利用的数据资料。

2 计算方法与评价指标

2.1 计算方法

通过利用连云港51 a 长期连续波浪资料进行设计波高计算，并对计算结果、不同采样方法和不同分布函数的比较后发现，最优的组合方式应该是使用年N 大波法（N=8），利用三参数Weibull 分布函数结合最小二乘法进行计算（曹兵，2014）。

三参数Weibull 概率分布函数可以写成：

其中，X 是一个变量，比如风暴（灾害性天气过程引发的）历时或波高，X^是一个给定的值，P是当时的概率，α，β 和γ 分别为形状系数，尺度系数和位置系数，这些值由具体计算数据确定。

用线性拟合来确定Weibull 分布函数中的β 和γ，则Weibull 分布函数（1）要写成线性形式：

其中，W 称为Weibull 的简化变量，β 和γ 仍可通过线性回归分析确定，α 则需要通过试算来确定，α 的值是由线性回归分析中相关系数R2最大时确定，具体方法可参见（曹兵等，2007a）。

β 和γ 的值确定后，再根据一定重现期TR对应的设计累积频率P（考虑影响频次λ，本文中即λ=8），求出重现期对应的设计波高，计算公式为公式（3）、（4）。

2.2 评价指标

对计算结果的评价主要从3 个方面进行讨论，分别为置信区间、相关系数和均方误。

（1）置信区间

总体均值和标准差的估计为点估计，因为只能求出一个估计值。在实际工作中，需要对总体均值和标准差的存在范围以一定概率作出估计，成为区间估计。而把估计的概率称为置信水平，也称置信概率，把估计出的存在区间称为置信区间（印凡成，2000）。

置信区间的宽度大小与所选取置信水平有关。在样本量相同的情况下，置信水平越高，置信区间越宽。在置信水平相同的情况下，样本量越多，置信区间越窄，结果越可信。本文选取的置信水平为95%。根据41 种情况，可得置信区间结果，见表1。

由表1 可以看出，使用11～19 a 资料时，置信区间在0.05～0.06，其中14 a 时置信区间最大，达0.06；使用20～26 a 资料时，置信区间在0.04；27～37 a 资料时，置信区间在0.03；38～51 a 资料时，置信区间在0.02。

图2 不同年限下样本均方差与置信区间

由图2 可知，资料年限为11～14 a 时，均方差和置信区间出现上升过程；15 a 以上资料年限时，均方差出现逐渐下降的过程；当资料年限多于38 a时，均方差与置信区间逐渐趋于平缓。

总体来说，对于使用每年8 个大波的采样方法，15 a 以上资料年限的情况下，置信区间都很小。当然，使用资料年限越多，样本点越多，置信区间越窄，说明计算结果分布在真实设计值附近的概率越高，计算结果较为可信。

表1 不同资料年限的置信区间

（2）相关系数

为直接说明相关的密切程度，需根据相关程度特征值相关系数，相关系数表示为：

相关系数R2的范围是0～1，系数越大，说明相关性越好，就是直线拟合的越好。

（3）均方误

用来衡量观测点与回归线估计值之间的离差，用Sy表示：

y表示xi在回归线查得的纵坐标值。均方误愈小，说明回归线与观测点越接近；均方误愈大，说明回归线与观测点离得越远。

3 结果分析

3.1 计算结果分析

经对推荐的最优组合，即采用每年8 个的采样方法，结合三参数Weibull 分布函数，针对不同资料年限（11～51 a），共计41 组情况，列表2 和图3，并进行讨论。

由表2 和图4 不同年限下的设计波高可以看出，11～14 a，设计波高快速上升，14 a 时到达最大值；15～31 a，设计波高呈现缓慢下降的过程；32～46 a，设计波高存在较大波动；≥47 a，设计波高呈现缓慢上升趋势。

3.2 评价指标

由表2、图3 以及图5 不同年限下的相关系数和均方误图可以看出，11～14 a，相关系数与均方误波动比较厉害，很不稳定；15～21 a，相关系数出现缓慢上升的过程，均方误出现快速下降过程；22～30 a，相关系数与均方误都出现相对稳定的过程；31～46 a，相关系数存在较大波动，而均方误仍保持相对稳定的过程；≥47 a，相关系数呈现快速上升趋势，同时均方误出现快速下降趋势。同时，可以看出，资料年限使用51 a 时，得到相关系数最大，而均方误最小，因此使用51 a 资料年限进行的设计值最为可信，同时佐证了表3 给出的值是可信的。

3.3 与设计参考值比较

以51 a 资料计算得到的设计值作为参考标准（表3），针对不同年限的设计值进行评估，见表4和图6-图7。

由表4 和图6～图7 情况可以看出：11～14 a，误差值快速减小，H100（百年一遇）设计值的相对误差由23.0%减小到2.4%，H50（五十年一遇）设计值的相对误差由21.8%减小到2.5%，H20（二十年一遇）设计值的相对误差由20.3%减小到2.2%；15～18 a，误差出现一个较小的过程，也就是设计波高计算值与推荐值出现接近过程，H100设计值的相对误差在0.4%～1.8%，H50设计值的相对误差在0.7%～1.4%，H20设计值的相对误差在0.7%～1.0%；19～31 a，误差呈现缓慢增大的过程，H100设计值的相对误差由3.4%缓慢增大到11.7%，H50设计值的相对误差由2.9%缓慢增大到10.3%，H20设计值的相对误差由2.0%缓慢增大到8.3%；32～46 a，误差存在较大波动，H100设计值的相对误差在3.7%～14.8%之间振动，H50设计值的相对误差在3.4%～13.2%之间振动，H20设计值的相对误差在3.3%～11.0%之间振动；≥47 a，误差值呈现减小趋势。

3.4 综合分析结果

根据不同资料年限计算结果以及与推荐设计值的比较后综合分析，资料年限少于15 a，设计波高变化较大，误差变化大，相关系数与均方误评价指标不稳定，结果不可信；15～18 a，设计波高相对稳定，误差有一个较小的过程，而评价指标处于快速趋于稳定期；19～21 a，设计波高处于缓慢减小过程，误差处于缓慢增大过程，评价指标处于趋于稳定过程，结果趋于可信过程；22～30 a，设计波高处于缓慢减小过程，误差处于缓慢增大过程，评价指标较稳定，因此结果较可信；31～46 a，设计波高、误差存在一定的波动，评价指标也不太稳定，结果存在一定的不确定性；当资料年限多于47 a 时，设计波高出现缓慢上升趋势，误差逐渐减小，而评价指标则趋于优化的方向，此时结果最优。

为便于分析和展示不同资料年限下结果的可用性，现将上述分析的设计值结果、相关系数与均方误、设计值误差分析、综合评价等评价结果列出，见图8。其中，分项评价指标中黄色表示该资料年限不可信，浅蓝色表示该资料年限结果一般，蓝色表示该资料年限结果较好，深蓝色表示该资料年限可信。综合评价结果由3 个评价指标取最不利情况得到，11～14 a 以及31～46 a 结果为黄色，表示不可信；15～18 a 结果为浅蓝，表示该年限得到的结果一般，在年限不足情况下尚可使用；19～21 a 结果为蓝色，表示该年限结果较好，趋于可信过程；22～30 a 以及47～51 a 结果为深蓝，表示该年限结果好，推荐使用。

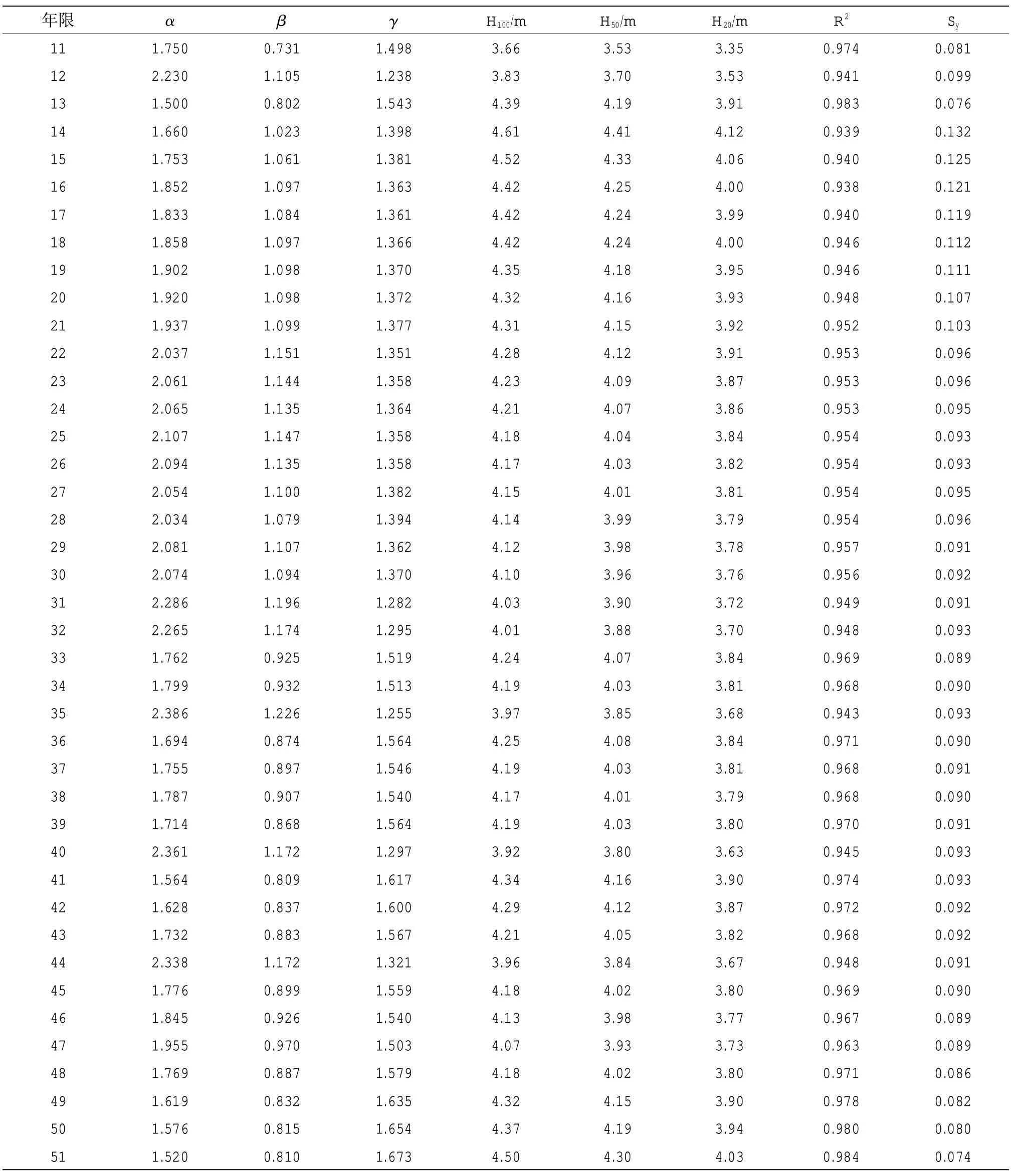
表2 最优组合不同年限下的计算结果

图3 最优组合下不同年限分布函数曲线示例

图4 不同年限下的设计波高

图5 不同年限下的相关系数与均方误情况

表3 连云港海域设计波高结果

图6 不同年限下的设计波高绝对误差情况

图7 不同年限下的设计波高相对误差情况

由此，对于中长期资料年限，19～30 a 结果相对稳定可靠，可作设计计算；对于长期资料年限，47 a 以上资料更为合理，结果更可信。

表4 不同年限下设计值的绝对误差和相对误差结果表

3.5 满足设计要求的最少年限

如果计算百年一遇的设计波高时，若能收集到超过一百年的波浪观测资料，那么只需进行频率分析，即可确定重现期对应的设计波浪值，而现实中往往只有时间较短的资料年限。

通过对3.4 节资料年限分析比较，可以得到，对于长期资料年限，使用年限47 a 以上的资料较为合理，对于中长期资料年限，19～30 a 资料较为稳定。因此，在计算重现期较大的设计波高时，建议使用较长的资料年限。对于计算百年一遇的设计波高值时，使用年限47 a 以上的资料较为合理，结果较为可信；对于计算五十年一遇的设计波高值时，使用年限19～30 a 的资料较为合适，结果能满足设计的准确和精度要求，至少也得19～22 a；对于计算二十年一遇的设计波高值时，使用年限也至少需要15～18 a，详见表5。

表5 满足设计要求的最少年限

有些规范（海港水文规范，2013；CEM，2002等）规定，连续资料年数不宜少于20年，由此处分析可知，当计算二十年一遇与五十年一遇重现期的设计波高值时，20年资料序列已能满足精度要求。但当计算一百年一遇或更长重现期的设计波高值时，20年资料序列则不能满足计算结果的精度要求，故建议使用更长时间序列的资料。

S.王等（1984）研究发现，当置信水平取90%波侯参数时，也即最不利情况下，重现期为二十年一遇、五十年一遇及一百年一遇的最少资料年限分别为7～10 a、14～21 a 及25～37 a，另外，资料年限由30 a 延长到50 a 得到的增益好象不大。

因此，本文的研究成果中所需最少年限要比S.王等研究结果所需的年限稍多，可能在于本文的置信水平为95%，要求更为严格所致。另外，本文认为47 a 以上的资料年限获得的计算结果，要比20～30 a 资料年限获得的计算结果更为可信。

同时，可以看出，当有15～18 a 时间序列资料时，可推算1.0～1.5 倍时间序列对应时间长度的重现期；当有19～50 a 时间序列资料时，可推算2.0～2.5 倍时间序列对应时间长度的重现期。

图8 不同评价指标下各资料使用年限的可用性评价结果

4 结论

本文利用连云港海域1960-2011年（1964年缺失）连续51 a 长期波浪资料，针对不同资料年限共计41 组情况，结合以往研究成果中适合连云港海域的采样方法和分布函数的最优组合，即年N大波法（N=8）和三参数Weibull 分布函数，应用最小二乘法进行了拟合。文章通过对设计波高值结果、置信区间、相关系数、均方误等评价指标进行了分析，与设计参考值进行了比较，并进行综合评价，从而得到了更优的资料使用年限与满足精度要求的最少年限等内容。

研究结果表明，在连云港海域，对于中长期资料年限，19～30 a 结果相对稳定可靠，对于长期资料年限，47 a 以上更为合理，结果可信。同时给出计算一百年一遇重现期时47 a 以上资料较为合理，五十年一遇重现期时19～30 a 较为合适，最少也得19～22 a，二十年一遇重现期时至少需要15～18 a。

C Guedes, Soares M G Scotto, 2004. Application of the r largest-order statistics for long -term predictions of significant wave height，Coastal Engineering,51:387-394.

Coastal Engineering Manual (CEM), 2002. Chapter 8:Hydrodynamic analysis and design conditions. U S，Army Corps of Engineers，Coastal and Hydraulics Laboratory.

Smith R L, 1986. Extreme value theory based on the r largest annual events,Journal of Hydrology,86:27-43.

You Z J, Jayewardene I, 2003. Prediction of the occurrence of extreme coastal storms along the NSW coast, National Environment Conference,IEAust,Brisbane,389-392.

You Z J, Lord D,2005.Influence of the El Nino Southern Oscillation on storm severity along the NSW coast. 17th Coastal and Ports Australasian Conference,IEAust,Adelaide,535-539.

You Zai-jin, Yin Bao-shu, 2006. Estimation of Extreme Coastal Wave Heights from Time Series of Wave Data,China Ocean Engineering,20(2):225-241.

S 王，B L 美哈乌特黄瑞兰，1984.观测年限和长期波浪统计，华水科技情报，（2）：83-92.

曹兵，王义刚，Zai-Jin You，2006.三种计算设计波高方法比较，海洋工程，24（4）：75-80.

曹兵，王义刚，YOU Zai-jin，2007a.设计波高分布函数比较，海洋湖沼通报，114：1-9.

曹兵，2007b.极值波高统计分析方法比较研究，南京，河海大学.

曹兵，徐常三，高清清，等，2014.连云港海域极值波高统计分析方法研究，海洋通报，33（1）：6-14.

王志旭，陈子燊，2013.极值波高Weibull 分布的参数估计方法对比分析，海洋通报，32（2）：127-132.

印凡成，夏乐天，2000.概率论与数理统计.南京：河海大学出版社.

中华人民共和国交通部，2013年. 海港水文规范（JTJ145-2-2013），北京：人民交通出版社.